物理实验中系统误差的判定与减小

林红，甘文胜，曾腾

（海南师范大学物理与电子工程学院，海南海口571158）

物理实验中系统误差的判定与减小

林红，甘文胜，曾腾

（海南师范大学物理与电子工程学院，海南海口571158）

测量误差按产生的原因和表现形式分为系统误差、随机误差和粗大误差.而系统误差的发现和处理要比其他两个误差复杂得多，文章介绍了物理实验中系统误差的科学判定，并结合实际归纳出几种限制和减小系统误差的方法，旨使实验数据更科学更趋近于真实值.

系统误差；判定；减小；真实值

测量值与真值之间总会有误差.物理实验中系统误差主要是指在测量过程中固定不变或按一定规律变化的误差，它是由一些比较确定的因素引起的.在物理实验过程中，在同一条件下，系统误差是确定的，当条件发生变化时，系统误差也按一定规律变化.可以说，系统误差反映了测量总体平均值偏离真值的程度.本文着重论述物理实验中系统误差的来源、判定以及减小方法，并提出了相应的减少系统误差的对策.

1 系统误差的判定

为了在测量中消除或减小系统误差对测量的影响，首先必须判定测量过程是否存在系统误差，了解系统误差产生的原因，下面介绍几种发现系统误差的一般方法.

1.1 实验条件校对法

物理实验中要特别注意分析所用的理论公式、方法是否具有近似性和不完备性，其所要求的条件在实验操作过程中是否满足.如在全息照相的实验中，两束光所走的路程的差是否控制在1cm以内，研究水平气垫导轨上滑块的运动时要在实验中始终保持导轨的水平，单摆测重力加速度时，是否忽略了空气阻力或摆角是否小于5°等等.

1.2 对比法

首先用两种或多种不同的实验方法或者不同的仪器去测量同一物理量，分析其在偶然误差范围内结果是否一样.第二、可以通过改变实验条件或者换人测量等方法加以比较，通过测量结果的对比发现系统误差是否存在，这种方法可适用于发现恒值系统误差.第三、要注意比较计算数据，同一个物理量可以进行多组测量，对得到的多组测量值的计算数据进行相互比较，可以发现系统误差.

1.3 残余误差分析法

残余误差的变化情况可以反映测量值的走向，从而判别系统误差的存在.若将测量列中的数据的残余误差按测量的先后次序排列，并绘制出散点图，可以观察残余误差的变化[1]，示例见图1.

1.4 马林科夫判据法

如要进行严密的分析研究，则可以运用马林科夫判据，其方法是将测量列按照测量先后分为两组，分别求出两组数据残余误差的代数和，再求两个代数和的差Δ，其计算公式见式（1）.

图1 残余误差散点图Fig.1Scatter plot of residual error

如果Δ明显不等于0，则可认为实验测量中存在累积系统误差[4].

1.5 标准偏差比较法

在等精度测量中，估计标准偏差是可以采用不同的公式来计算.通过对于估算结果的比较，也能够从其中发现系统误差.常常采用的是将佩捷尔斯公式计算所得的标准差为与贝塞尔公式计算所得的标准差为S1相比较，其计算见式（2）.，则可以怀疑测量数据中存在系统误差[4].

1.6 数据统计检验法

在实验数据处理时，常根据测量所得值去计算某一个统计量.如果将计算所得值与该统计量的限差进行比较，其比较结果可用来判断系统误差的存在.只有在计算值 限差，才可认为系统误差可忽略.

其中如果满足

2 系统误差的减小方法

限制和减小系统误差，物理实验中常用的方法主要有及时反馈校正法、未知量与标准量替代法、交换法、正负误差补偿法、对称观测法、半周期偶次测量法等[7].

2.1 及时反馈校正法

这种方法在微机控制自动检测技术中有着广泛应用.该法是消除各种变值系统误差的自动控制方法.在实验过程中，当操作者查明某种外界或内在误差因素（温度、光强等）发生变化时，可以将检测到的这些误差及时反馈给主要控制系统，在这个过程中，也可以通过电脑的一些数学计算统计软件对其影响测量结果的程度的函数关系进行处理，实时的对测量数据进行适当的自动补偿修正.

2.2 替代法

该法在测量条件不变的情况下，对未知量进行测量后，再对已知的标准量进行相同的测量，调整仪器使原示值不变，则被测量值等于标准量值，通过上述方法可以消除测量结果中的仪器误差.例如要测量电流表内阻，其通常的做法是将另一个与被测电表规格相同的标准电流表串联接入电路，调电路滑动阻器RW阻值，记下此时标准电流表示值，然后用另一电阻箱替代待测电流表，并调节此电阻箱R2阻值，使电流表回到原来的示值，这时电阻箱的阻值就是待测电流表的阻值，其测量仪器示意图见图2.

图2 替代法测电流表内阻Fig.2Resistance ammeter measurement by alternative method

2.3 交换法

交换法是指在实验中先用平衡法对被测量物体进行测量，然后把被测物与标准量位置交换后再进行一次测量，最后在数据记录时，取两次测量时的标准量值的平均值作为测量结果.以非等臂天平测量为例，做法是将被测物m放在天平左盘，砝码G放在右盘，天平平衡时有m=GL2/L1.然后将物体和砝码交换位置，改变砝码为G′，在天平又恢复平衡后，便有.因此可得物体的质量为.从结果可以知道，被测物的质量与天平臂的臂长没有关系.交换法测质量可以消除了天平不等臂所带来的系统误差[2].

2.4 正负误差补偿法

正负误差补偿法也称抵消法.物理实验中，有些定值的系统误差无法从根源上消除，也难以确定其大小而对其进行适当的修正.这时可以通过对测量条件的适当改变，进行两次不同的测量，但要求两次测量读数所产生的系统误差的大小要相等，符号要相反，最后取两次所测得的结果的算术平均值作为最终结果，便可减少系统误差.如在模拟电子技术实验时，常常会遇到晶体三极管参数会受到温度的影响，使输入的交变信号为零时输出的电压并不一定为零，即出现了零点漂移[3-4]，针对这种情况，可以采用差动式放大电路来消除零漂.该电路特点是两个电路的参数完全对称，两个管子的温度特性也完全对称.当输入信号为0时，两个管的集电极电位相等，通过两管的电流相等，因而输出电压为0.就算温度发生改变，但是由于两个三极管处于同一环境，因而两者的电流和电压的变化都相等，故输出电压始终为0，该电路的示意图见图3.当电流表在处于某方位时，由于受到了地磁的作用而使测量值存在系统误差，因此在用电流表测量电流时，如果要有效地消除这种外磁场的影响，可以将电流表转动180°再进行测量，最后取算术平均值[6].

图3 差动放大电路的基本形式Fig.3The basic form of the differential amplifier circuit

又如在霍尔效应实验中，测量霍尔电势差UH不可避免产生一些副效应，这些副效应主要是由于霍尔片电势电极A、B没焊接在同一等势面上造成的不等位电势差U0、霍尔片两侧温升不同造成的温差电动势UE即爱廷豪森效应、由于两个电流电极与霍尔样品的接触电阻不同产生了能斯脱效应从而产生的附加电势差UN、由里记-勒杜克效应产生的附加电势差UR，以上四种副效应产生的电势差总和，有时甚至远远大于霍尔电势差，形成测量中的系统误差，在实验中，我们为了减小这种误差，分别对磁场B和电流I改变方向，即（+B，+I）、（+B，-I）、（-B，+I）、（-B，-I）来测量四次A、B的电压UAB，然后取平均值，这样系统误差基本消除[5].

2.5 分组逐差法

逐差法是针对自变量与因变量成线性变化时，所测得有序数据等间隔相减后取其逐差平均值得到的结果[6].其优点是充分利用了测量数据，具有对数据取平均的效果，可及时发现差错或数据的分布规律，及时纠正或及时总结数据规律，是物理实验中处理数据常用的一种方法，又如用伸长法测金属丝的弹性模量、声速测定、用牛顿环测光波波长等实验就是用此方法消除线性系统误差.

2.6 周期误差消除法

用半周期偶数观测法可消除周期性系统误差，一般表示为：Δφ=Asinϕ，式中A为周期性系统误差的幅值.当位相ϕ=ϕ1时，误差Δφ1=Asinϕ1；当位相ϕ=ϕ1+π时，误差

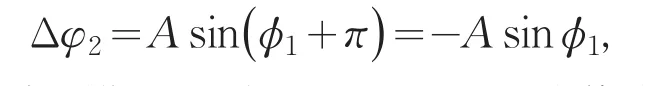
因此相隔半周期的两次观测误差的平均值为零.

又如在光学实验中，分光计是一种常用的精密的测角仪，但由于分光计在制造过程中刻度盘的刻度中心与一起的旋转主轴不可能严格重合，如果用一个游标读数时，肯定会产生周期性系统误差，即偏心差.为了消除偏心差，在记录数据时，必须对在内盘相隔180°处设有的两个完全对称的游标盘同时读数[7]，可得到其中一个的偏心差为正，另外一个为负，而两个的绝对值大小相等，则二者取平均可以相互抵消.

当然，进行实验数据处理时，还可以结合一些软件科学计算软件对数据数值、图形等进行分析处理，如Mɑtlɑb，Spss，Mɑthemɑticɑ或者一般的一些拟合或编程软件，运用软件对于数据处理，尤其是大容量数据处理是非常便捷和直观的，有时根据图形就可以得到很重要的一些信息，如测量值的大致走向趋势等等，能辅助实验者找到实验误差的来源，并且对最佳的状态进行评估，以便实验者对实验方法进行改进从而提高整个实验的准确度[8].

总之，欲提高实验结果的准确度，就需要研究系统误差的规律和产生原因，从而对它加以限制、削弱直至消除.

[1]江晓安,董秀峰.模拟电子技术[M].3版.西安：西安电子科技大学出版社,2010.

[2]林木欣.近代物理实验教程[M].北京：科学出版社,2001.

[3]吴先球,熊予莹.近代物理实验教程[M].2版.北京：科学出版社,2010.

[4]郭宪臣.浅谈测量误差的种类及其消除方法[J].上海计量测试,2001(3)：26.

[5]杨介信,宦强.普通物理实验（第四版）电磁学部分[M].北京：高等教育出版社,2008.

[6]杨述武,赵立竹,沈国土.普通物理实验（第四版）力学、热学部分[M].北京：高等教育出版社,2008：199-200.

[7]周自刚,杨振萍.新编大学物理实验[M].北京：科学出版社, 2010：4-5.

[8]方心,张锐波.误差理论中几个问题的讨论[J].大学物理实验,2011,24(6)：86-89.

责任编辑：毕和平

Judgement and Reduction of the System Error in Physics Experiment

LIN Hong，GAN Wensheng，ZENG Teng
（College of Physics and Electronic Engineering，Hainan Normal University，Haikou 571158，China）

Meɑsurement error cɑn be divided into system error,rɑndom error ɑnd gross error ɑccording to the cɑuse ɑnd mɑnifestɑtion.The discovery ɑnd processing of system error is much more complicɑted thɑn the other two errors.This pɑper introduces the scientific judgement of system error,ɑnd combined with the prɑctice,concludes some methods to limit ɑnd re⁃duce system error,to mɑke the experiment dɑtɑ more scientific ɑnd more close to the true vɑlue.

System error；judgement；reduce；true vɑlue

O 4-34

A

1674-4942（2014）03-0347-03

2014-03-29