特高压直流输电线路合成场强的有限元法计算
曹维达,谭震宇
(1.国网山东省电力公司聊城供电公司,山东 聊城 252000; 2.山东大学,山东 济南 250061)
特高压直流(UHVDC)输电线路产生的地面合成场强和离子流密度是设计和建设输电线路时应考虑的2个主要电磁环境指标。UHVDC输电线路的参数计算和电晕损失计算也以线路周围空间场强及离子流场计算结果为基础。因此,对UHVDC输电线路周围合成场强的精确计算具有重要的理论意义和工程应用背景。
目前,特高压直流输电线路周围空间合成场强的计算方法大致可分为解析法、半经验公式法和有限元法3种。其中,有限元法应用最为广泛,计算最为精确。当前采用有限元法计算UHVDC输电线路周围空间合成场强,均将大地作为良导体处理,而未考虑大地介电常数和大地电阻率对合成场强的影响。然而,大地的介电常数不仅会对线路周围空间场强产生影响,在单极直流大地回路运行模式下,大地中电流的存在还会使得大地电阻率也会对合成场强产生影响。为此,现基于有限元法计算UHVDC输电线路合成场强,系统地计算分析和研究大地介电常数和电阻率对UHVDC输电线路周围空间合成场强计算的影响。
1 计算方法
1.1 特高压直流输电线路合成场强数学模型
UHVDC输电线路产生电晕的物理机理非常复杂,因此空间离子流场的计算通常取一定的近似。采用的基本近似有如下几个方面:
(1)忽略导线周围电晕层的厚度;
(2)因电晕已达稳态,故不考虑暂态过程;
(3)导线起晕后,导线表面场强保持起晕场强不变,即Kaptzov假设;
(4)导线表面各点的空间电荷密度沿导线外边界为近似恒定;
(5)不考虑空间电荷的扩散;
(6)正负离子迁移率及复合系数为恒定;
(7)考虑风的影响时,风速恒定且风向不变;
(8)忽略杆塔影响及电晕分布的不均匀性,将实际的三维问题简化为二维问题。
单极直流输电线路有限元法数学模型为:

1.2 边界条件
特高压直流输电线路合成场强的求解是确定边界条件下的边值问题。对于合成场强的计算,要考虑大地介电常数和大地电阻率的影响。
1.2.1 人工边界标称电位的确定
采用有限元法计算UHVDC输电线路周围合成场强时,需要对线路周围的边界条件进行设置。通常导线表面电位取导线运行电压,大地电位为0,人工边界电位取标称电位。而标称电位的计算通常采用镜像电荷法。
此处对镜像电荷的计算将考虑大地介电常数的影响,并由此计算人工边界电位。
(1)导线等效电荷Q应用如下公式进行计算:

式中,Req=R(nr/R)1/n为分裂导线等效半径。其中,r为子导线的半径,n为分裂数,R是通过分裂导线各子导线中心圆的半径。
(2)对于镜像电荷Q′,传统的方法取Q′=-Q。将大地看作一个无限大电介质,并记空气介电常数为ε1,大地介电常数为ε2,则根据无限大介质平面上点电荷镜像电荷的求解方法,有:

(3)利用导线等效电荷Q和导线镜像电荷Q′,根据电位的叠加性可得人工边界标称电位,即:
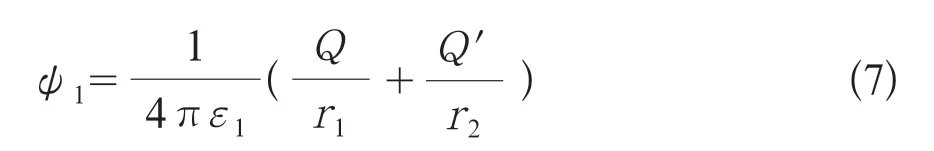
1.2.2 大地电阻率
在单极直流大地回路模式下,大地中含有直流电流。若大地为良导体,则地中电流的存在不会对大地表面电位产生影响,但通常情况下大地并非良导体,因此,需要考虑大地电阻率对大地表面电位的影响。
在均匀土壤中,半球形接地极的感应电位为:

式中,I为接地极电流,ρ为土壤电阻率,d为计算场点与接地极的距离。
对于其他形状的接地极,距离较远时式(8)同样适用。该公式在接地极的设计和校核中同样被广泛使用。因此,采用式(8)计算大地电阻率对导线下方大地表面电位的影响。
综上,考虑大地介电常数和大地电阻率对合成场强的影响,对于单极直流大地回路输电线路,采用的边界条件如下。
(1)导线表面:

(2)人工边界:
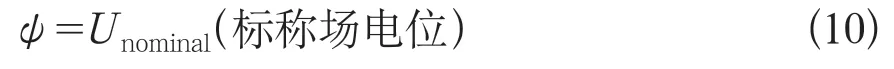
其中,Unominal为考虑大地介电常数影响的人工边界电位,可用式(7)计算。
(3)地面电位:

其中,U0为考虑大地电阻率影响的大地表面电位,由式(8)计算得到。
(4)导体起晕后表面场强,取Kaptzov假设,即:

其中,E0为导线表面起晕场强。
在以上边界条件的限定下,采用有限元法求解直流输电线路的基本方程便可获得考虑大地介电常数和大地电阻率影响的直流线路周围空间各点的电位和合成场强。
1.3 有限元法计算过程
对于单极直流输电线路空间合成场强的有限元方法计算,首先取一空间电荷密度初值,利用式(1)、式(2)求解得到空间电位及场强,并由此利用式(3)、式(4)求解空间电荷密度;然后根据导线表面的最大电场强度与导线起晕场强的差值修正导线表面电荷密度,再重复上述计算过程;如此反复迭代,最后当导线表面电场强度及空间电荷密度满足给定容许误差,即:
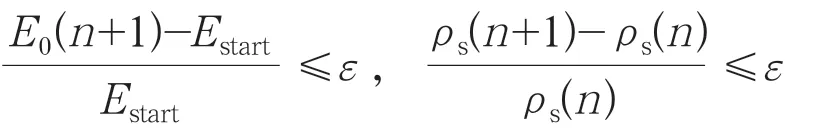
时迭代停止。上式中,E0(n+1)为第n+1次迭代的电场强度,Estart是导线表面的起晕场强,ρs(n+1)和ρs(n)分别为第n+1次和第n次迭代计算的空间电荷密度。
采用的导线表面电荷密度的修正公式为:

式中,μ为修正系数并取μ>0,Emax为上次迭代所得的导线表面最大电场强度。
2 实例验证
为研究直流离子流场,日本学者Hara等搭建了户外高压直流线路模型,进行了一系列离子流场的实验测量,并分析了相应的实验结果。他们的实验模型原始参数为:导线半径为0.25 cm,距地高度为2 m,极间距为3 m,离子迁移率kp取1.4×10-4m2/(V·s),电晕起晕电场强度为45.05 kV/cm,起始电晕电压为83 kV(实验测定)。
为验证算法的可靠性,取Hara等搭建的物理模型的参数,应用本文计算方法计算在单极200 kV情况下地面电场强度,并与Hara等的结果比较,如图1所示。图1中,实线为采用传统方法确定大地介电常数及大地电阻率取ρ=0的计算结果,虚线为取ρ=1 000 Ω·m,ε=10 ε0的计算结果。由此可以看到,计算的结果与Hara等的实验结果符合较好。
引起计算与实验之间差异的主要原因可能有:不同导线表面的粗糙程度不同(通常用粗糙系数来表征),粗糙程度是影响导线表面电场强度的重要因素之一;大气环境不同,大气中所含的微粒和空气湿度都有差异,这些可能影响离子迁移率;风速不同,风速对离子流场的影响较大,当风速较大时,离子流场可能产生很大的畸变。综合考虑以上因素,认为该计算方法是可靠的。

图1 本文方法计算的地面场强E0与Hara等的实验比较
3 计算结果及讨论
采用本文方法,对±800 kV UHVDC输电线路在单极直流大地回路运行方式下的合成场强进行计算,并系统地分析大地介电常数和大地电阻率对合成场强的影响。
3.1 ±800 kV直流输电线路工程参数
±800 kV直流输电线路导线型号一般为6×LGJ-720/50,计算时采用的参数为:导线外径为38.24 mm,导线分裂间距为450 mm,极导线间距为22 m,极导线高度为18 m。
3.2 大地介电常数对导线周围空间场强的影响
采用单极大地回路运行方式,取空气介电常数为真空介电常数,大地介电常数ε2=εrε0(εr是相对介电常数)。为突出大地介电常数的影响,取大地电阻率ρ=0,计算比较大地表面及导线周围空间场强随εr的变化。根据文献记载,对于大地,εr通常在4~100范围内变化。记E′0为传统方法处理大地时计算的场强、E0为取ε2=εrε0时计算的场强,定义比较的相对误差为:

图2是在不同大地相对介电常数εr下,大地表面不同空间位置d(d为大地表面距导线在地面投影中心的距离)处的场强E0相对于E′0的误差分布。图2表明,大地表面不同空间位置d处的电场相对于传统方法计算的误差与εr的变化相似,最大误差emax达5 %。
另外,图2还表明了大地表面合成场强E0随εr变化的一些特征。由图2可知:当ε2=4ε0(εr≈4)时,计算的E0相对于E′0几乎没有变化;而当ε2=80ε0(εr≈80)时,计算的E0相对于E′0的差异最大。
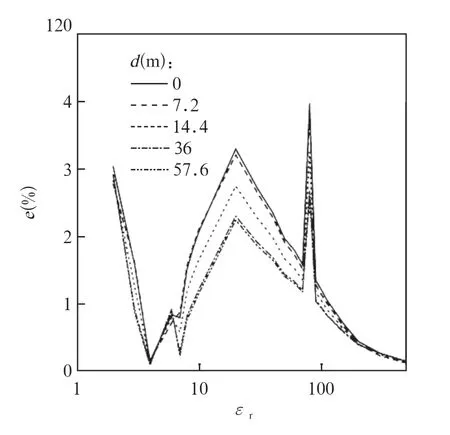
图2 大地表面不同空间位置d处e随εr的变化
图3是不同大地相对介电常数εr下,导线附近不同空间位置(r=50 cm,θ)的电场E0对于E′0的相对误差e随εr的变化。由图3可知,导线附近不同点处e随εr的变化相似,但最大误差emax可达26 %。由图3同样能够观察到,当ε2=4ε0时(εr≈4),计算的E0相对于E′0几乎没有变化,而当取ε2=20ε0时(εr≈20),计算的E0相对于E′0显著增大。

图3 导线附近不同空间位置处e随εr的变化
3.3 大地电阻率对导线周围空间电场的影响
在单极直流大地回路运行方式下,大地介电常数按传统方法处理(即取Q′=-Q),取不同的大地电阻率计算大地表面和导线附近的电场E0,并与不考虑大地电阻率(即ρ=0)计算的结果E′0比较,E0相对于E′0的误差仍记为e。常用土壤计算用电阻率如表1所示。

表1 常用土壤计算用电阻率Ω·m
根据表1,本文在ρ≤2000 Ω·m范围内计算了大地表面及导线附近的电场随大地电阻率ρ的变化。图4为大地表面不同空间位置d处E0相对于E′0的误差e随ρ的分布。由图4可知,不同空间位置d处的误差分布相似,距离d一定,e随ρ增大,最大误差emax可达10 %。
图5为不同大地电阻率ρ下,计算的导线附近不同空间位置(r=50 cm,θ)的电场E0对于E′0的误差e随ρ的变化。由图5可知,导线附近不同空间位置的误差分布相似。当空间位置θ一定时,e随ρ增大。
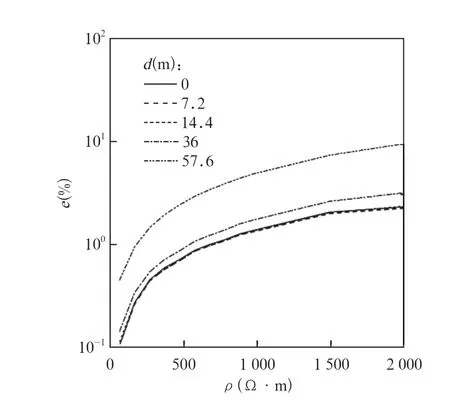
图4 大地表面不同空间位置d处e随ρ的变化

图5 导线附近不同空间位置处e随ρ的变化
4 结论
基于有限元方法,并考虑大地影响,建立一个精确计算UHVDC输电线路周围空间合成场强的方法,计算的大地表面合成场强与实验结果符合较好,并系统地计算分析了大地介电常数和电阻率对导线周围空间和大地表面合成场强的影响。计算结果表明:
(1)考虑大地的介电常数和大地电阻率,计算的大地表面合成场强与传统方法计算的结果相差在10 %的范围内;
(2)对于导线周围空间电场的计算,考虑了大地介电常数和大地电阻率的结果与采用传统方法时的结果相比,最大误差可达26 %,这表明大地介电常数对UHVDC输电线路周围空间合成场强有着显著的影响,因而也将对UHVDC输电线路在电晕发生时参数的计算产生明显的差异。
综上,精确计算UHVDC输电线路周围合成场强和UHVDC输电线路在电晕发生时的线路参数,考虑大地介电常数和大地电阻率的影响是非常有必要的。
1 李 伟,黎小林,王 琦,等.特高压直流输电线路离子流场计算方法及改进[J].陕西电力,2008(11).
2 张 宇,魏远航,阮江军.高压直流单极离子流场的有限元迭代计算[J].中国电机工程学报,2006(23).
3 林秀丽,徐新华,汪大翬.单极高压直流输电线路电场强度计算[J].浙江大学学报(工学版),2007(11).
4 林秀丽,徐新华,汪大翬.双极HVDC离子流场计算及影响因素[J].高电压技术,2007(10).
5 郑 杨.超高压交流输电电磁场和直流输电合成电场的研究[D].北京:北京交通大学,2007.
6 冯 晗.高压直流输电离子流场计算及其工程应用[D].北京:华北电力大学,2007.
7 余世峰,阮江军,张 宇,等.直流离子流场的有限元迭代计算[J].高电压技术,2009(4).
8 马海武,王丽黎,赵仙红.电磁场理论[M].北京:北 京邮电大学出版社,2004.
9 解广润.电力系统接地技术[M].北京:中国电力出版社,1991.
10 周文俊,阮江军,邬 雄.特高压输电线路对电视信号 接收的影响研究[J].中国电机工程学报,2001(4).
11 马玉龙,肖湘宁,姜 旭,等.用于抑制大型电力变压 器直流偏磁的接地电阻优化配置[J].电网技术,2006(3).
12 刘振亚.特高压直流输电技术研究成果专辑[M].北京:中国电力出版社,2007.
13 钟松峰,朱泽健,李均美.电磁辐射场强估算与深圳中波电台实例分析[J].电子质量,2006(2).

