油井单层含水快速识别油藏工程方法研究

聂 俊，孙德英，杨 东，张凤敏

(1.中国石化石油勘探开发研究院，北京 100083；2.中国石油大庆油田有限责任公司第四采油厂地质大队，黑龙江 大庆 163511)

水驱开发过程中，分层注水是调整挖潜、控制油田含水上升的基本技术手段。随着油田开发对象转移到渗透率较低的薄差储层，注水井数逐年增加，层段划分越来越细，分层含水量测试的工作量越来越大，常用的测试手段已经不能满足矿场实际生产的需要。找水法、C/O比能谱与中子寿命测井等方法，由于费用较高，不能大规模使用。而近年来受到重视的过套管电阻率测井，由于信号方面的问题也没有取得应有的效果。判别各层含水的直接测试方法测量到的是间接指标，还必须解释成含水率，在精度方面也存在较大误差。因此，该文尝试以油层静态参数和油水井连通关系等精细地质研究成果为基础，以渗流力学原理为基础，建立一种通过全井综合含水反求单层含水的数学模型方法，以满足油田进一步层系内注采结构调整的需要。

1 注水量劈分系数

对于井底流压明显低于泡点压力的情况，在油井附近形成脱气圈，此时对于每一注采对应层有物质平衡式为[1-3]：

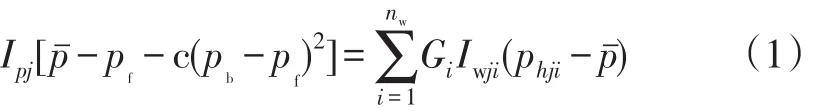
式中：pˉ为油井平均地层压力，MPa；pb为原油饱和压力，MPa；pf为油井流动压力，MPa；Ipj为油井各层采液指数，m3/（d·MPa）；c为原油物性和相对渗透率有关参数；Gi为各水井井网注入系数；Iwji为各水井单层吸水指数，m3/（d·MPa）；phji为各水井单层注入压力，MPa；nw为水井数。

求解上式，得：

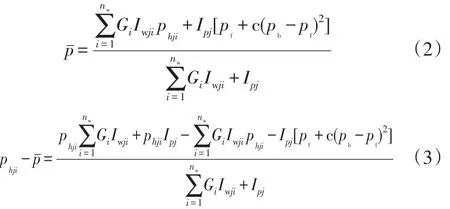
注采井网内总注入量为：

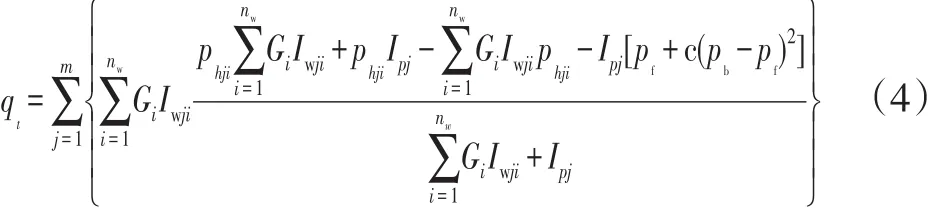
式中：m为注采井网内小层数。

第j层注水量为：

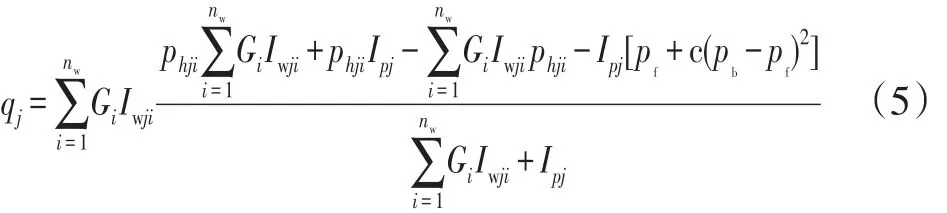
第j层段注水量劈分系数为：

2 含水上升规律方程

注入水流动过程中，形成一个水驱前缘。当水驱前缘突破以后，油井开始见水，随着开采的不断持续，含水率不断上升。含水上升规律可由油水两相渗流方程推导出来[4-5]。根据渗流力学等饱和度面移动方程可知，径向地层中水驱前缘速度方程可用下式表示：

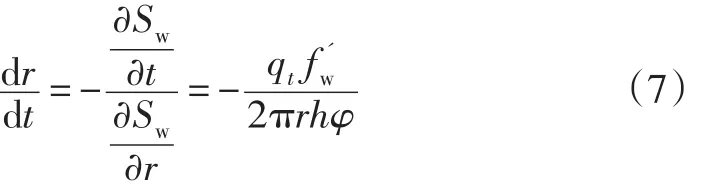
积分上式，并假设t=0时注入水仅在水井处，有：

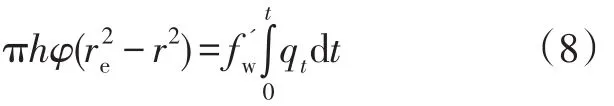
考虑到渗流区域并不完全是圆形的，上式可近似推广为：

式中：re为供给半径；S为油井泄流区面积。

在油井见水后，上式左边分子为常数，两边对t求导数，有：

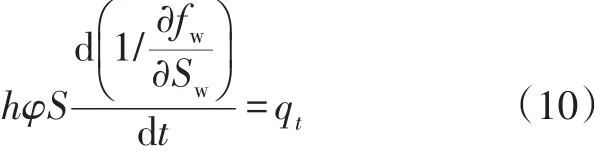
将上式展开：

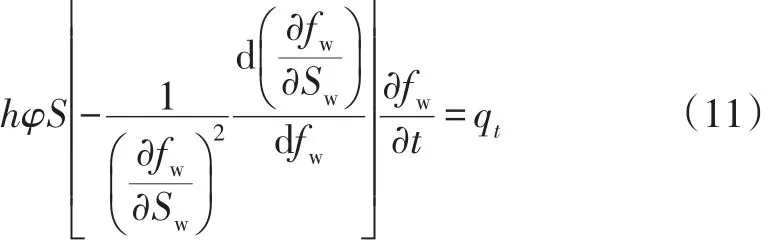
写成微分方程一般形式，有：

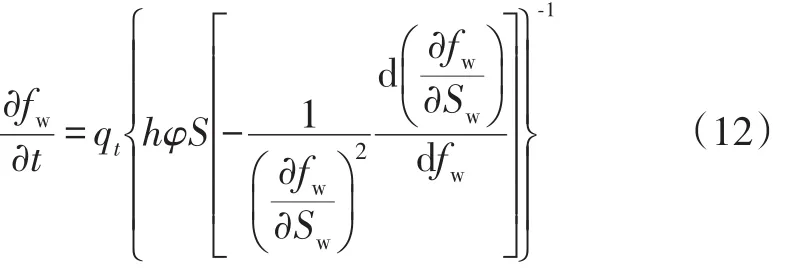
该微分方程描述了单油层含水上升规律。可以看出其主要影响因素是注水量、孔隙体积和相对渗透率曲线特征。以上式为基础，对于多层系统选择基准层（base），可得到各层含水相对变化微分方程，从而消除了时间过程的影响，进一步简化计算。

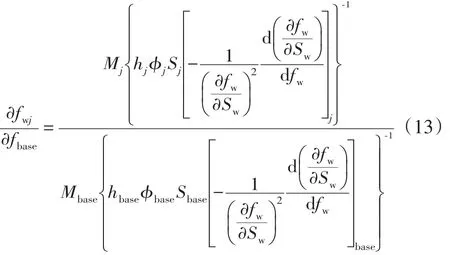
初始条件

式中：Mj为第j层注水量劈分系数；Mbase为基准层注水量劈分系数；fbase0为基准层初始含水率；fwj,0为第j层初始含水率。

公式（13）非线性微分方程，该文利用常微分方程的四阶Runge-Kutta方法进行求解。

3 微分方程含水率初值

求解（13）式非线性微分方程，需要以基准层见水时刻每层的含水率作为初始值。将见水时间最晚的层定义为基准层，得到基准层见水时间对应各层的含水率值即为求解（13）式所需的初始值。在求解过程中需要以油水相渗曲线为基础计算相应的指标[6]。

3.1 前缘含水饱和度计算

水驱前缘含水饱和度是计算水驱突破时间的关键参数。虽然用图形法可以求得这个参数，但是该文采用一种数值求解方法。水驱前缘含水率对含水饱和度的导数可以用下式来表示：

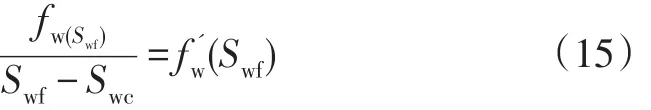
式中：Swf为前缘含水饱和度；Swc为束缚水饱和度。

上式是一个含有水驱油前缘含水饱和度的隐函数关系式，要求解（15）式，首先需要对相对渗透率曲线进行处理。统计结果表明，油、水相相对渗透率曲线可用以下函数表征：

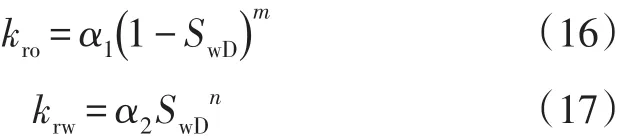
其中α1、α2、m、n为油水相渗曲线拟合系数，SwD为归一化含水饱和度，表达式为：

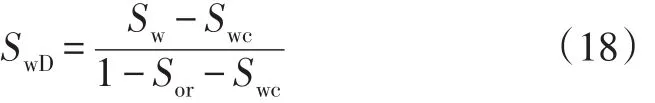
根据含水率的定义，可以得到含水率的表达式为：

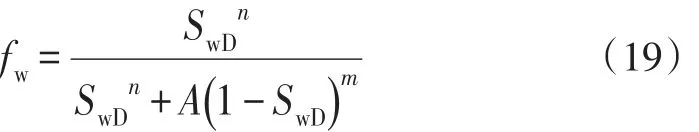
上式两边对含水饱和度求导，得到：

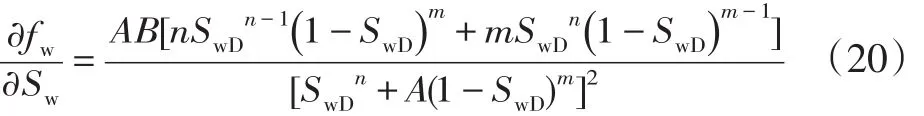
同时（15）式的左端可进行转化为：

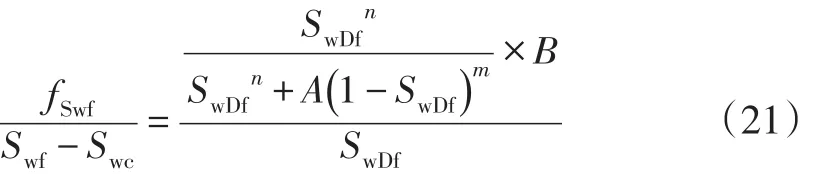
将（20）、（21）代入到（15）中可得：

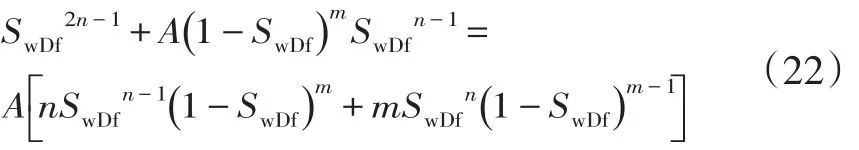
通过数值解法求解（22）的超越方程，解出SwDf，从而得到Swf、fw(Swf)以及基准层见水时刻含水率导数。

3.2 含水率与含水饱和度的生长曲线描述

研究表明：fw和Sw之间的关系可以用二次函数或者生长曲线来描述。实际上，由于生长曲线拥有有限的渐进线，与实际情况更为吻合，所以该文使用生长曲线进行拟合。

设含水率与含水饱和度的生长曲线描述表达式为：

上式两边取对数可得到：

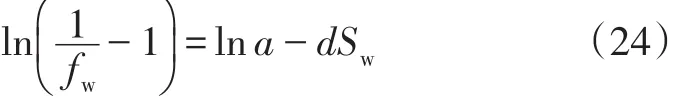
直线回归上式，求出斜率与截距后，即可求出系数a、d的值，从而得到含水率与含水饱和关系表达式。

3.3 微分方程初始值计算

对于恒定注入速度情况下，由（9）式可知第j层见水时间为：

式中：Tj为第j层见水时间，d；Sj为j层泄油面积,m2。

找出见水时间最大的层，将其定义为基准层（base）。同时，对于其余每一层，当t=Tmax时，即当基准层见水时，各层的含水率导数为：

同时，（23）式两边对含水饱和度求导，可以得到生长曲线含水率导数的表达式：

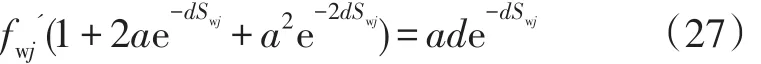
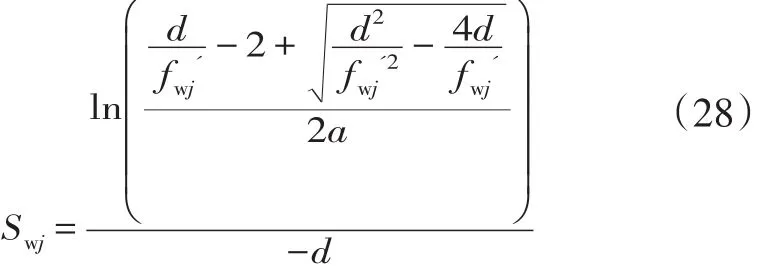
将上式计算得到的含水饱和度值代入到（23）式的生长曲线中，即可得到对应的含水率值。至此，求解（13）式非线性微分方程所需要的各层初始值就都得到了，可以用四阶Runge-Kutta方法对其求解。

4 分层含水率及剩余油潜力计算

设全井综合含水率为Fw，分层含水率分别为fwj，全井产液量为Q1t，产油量为Qot，分层产液量为Q1j，产油为Qoj则有：

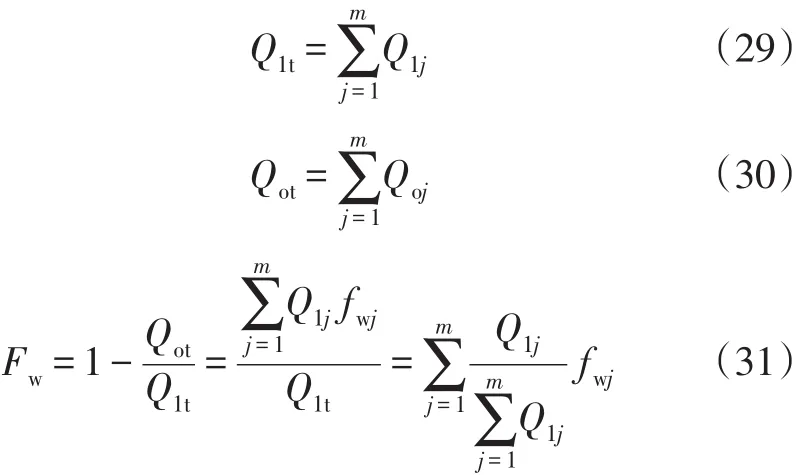
根据注水量劈分系数的定义，上式可以用下式表示：

将求解出的各层含水率与基准层含水率关系式带入上式，可以得到以基准层含水率为基础的综合含水率计算公式：

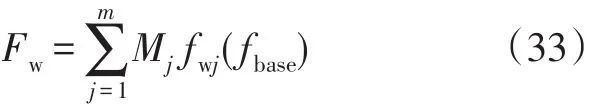
将（13）式非线性常微分方程求解结果和各层注水量劈分系数代入上式，可以计算出基准层含水率与全井综合含水率的对应关系。因此，给出全井综合含水率，就可以反求出基准层含水率，再将基准层含水率代入（13）式求解结果，即可求出所有层的分层含水率。

因此，假设给定油井的一个目前综合含水率为Fwnow，将其代入上述计算过程，可以求得每一层的含水率fwj。同时，在总注入量已知的情况下，根据计算得到的各层注水量劈分系数，可以求出每一层的注入量Qwj。据此，可以求出每一层的产油量：

计算出各层的含水率之后，根据求出的含水率与含水饱和度关系，可以非常方便地求出对应的含水饱和度，从而可以得到含油饱和度，按下述公式可计算各小层的剩余油潜力值。Opot值越大，对应的油层的挖潜潜力越高。

5 应用实例

将上述计算过程用Visual Basic语言编制了一套分层含水快速预测软件，并在大庆油田杏7区进行了应用。

大庆油田杏7区是典型的多油层非均质油藏，由于严重的层间非均质性，虽经过层系细分调整和多种工艺改造，但各油层含水差异仍然较大。搞清楚各单层含水情况是进一步控水挖潜的基础和前提。杏7区块积累了大量的精细地质资料，以此为基础，划分出了19个小层。将该区块的24口注水井和9口采油井划分成了9个注采单元。

以每个单元为基础，分别计算了注水量单层劈分系数和含水率预测图版。以第7井组计算得到的含水率预测图版为例（图1），预测图版中横坐标为基准层（第12层）含水率，纵坐标为含水率。图版绘制了从基准层见水时刻到含水率为100%时，各层及综合含水率的变化趋势。其中，红线对应不同小层的含水率变化情况；蓝线为全井综合含水率随基准层含水率的变化情况。很明显可以看出：第1小层的含水率增长是最慢的，含水率值也是最低的，这和其对应的注水量劈分系数也是最低的相一致。

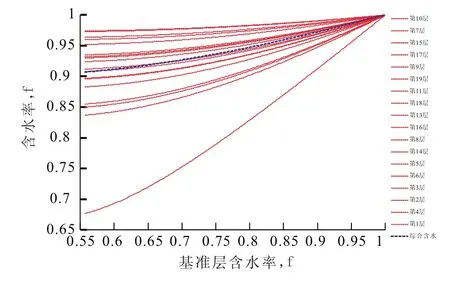
图1 杏7区块第7井组含水率预测Fig.1 Water cut forecasting chart of No.7 well group in Xin-7 block

在杏7区块综合含水率为93%的情况下，计算得到了每一小层的平均含水率、日产油量以及剩余油潜力值（表1）。

计算得到的各小层含水率值与现场C/O比测试方法解释得到的数据误差在10%以内。结合小层物性资料以及小层连通情况，对杏7区块各小层的潜力评价得到了如下几点结论：

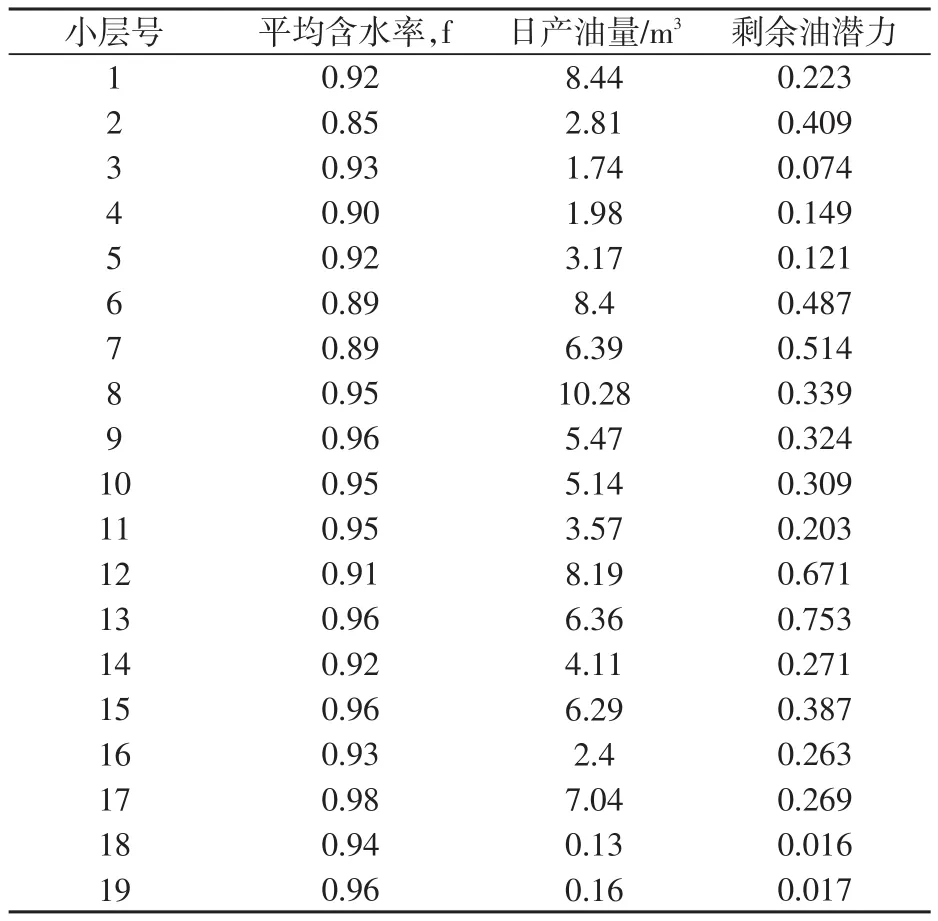
表1 杏7区块各小层生产情况统计Table 1 Production statistics of each layer in Xin-7 block

1）将19个小层按日产油量大小分成三类，第一类是高产量（日产油量大于5 m3）小层，这类小层有10层，储层物性和注采连通性都较好；第二类是中等产量小层（日产油量介于1～5 m3之间），这类小层有7层；第三类是低产量小层（日产油量低于1 m3），分别是第18和第19小层，这两个小层只在三个注采井组中连通性较好。

2）大部分小层的剩余油潜力都比较小，后期开发潜力最大的小层是第12小层和第13小层。

6 结论

1）以精细地质研究为基础，根据渗流力学原理建立的分层含水快速预测方法与传统的测试相比，大幅度节约了监测费用，极大地拓展了适用范围。

2）本方法适用于中高渗非均质多层注水开发油藏，尤其对高含水采油井进一步开展细分注水工作具有理论指导意义。

3）通过在大庆油田杏7区块的应用表明：与矿场实际找水资料相比，分层含水率的误差控制在10%以内，具有很好的推广价值。

[1]刘德华.油藏工程基础[M].北京：石油大学出版社，2011.

[2]唐曾熊.大庆油田注水开发[J].石油学报,1980,1（1）∶63-76.

[3]Klins M A.An improved method to predict future IPR curves[J].SPE 20724,1993,8(4)∶243-248.

[4]Hulme J R.Optimizing recovery from a strong water drive west Texas gas reservoir through integrated reservoir simulation studies[C].SPE 30716,1995∶127-141.

[5]P.T.法兹雷耶夫.油田面积注水[M].北京：石油工业出版社，1979.

[6]Pan Yan.Improved method for multivariate optimization of field development scheduling and well placement design[C].SPE 49055,1998∶249-264.