基于改进的距离判别分析法的电火工品感度性能预测方法
崔伟成,孙玉玉,刘林密,孟凡磊
(海军航空工程学院 a.飞行器工程系;b.政治部,山东 烟台 264001)
感度是电火工品的重要性能参数,通常采用感度上下限测试、升降法感度试验或感度曲线的方法判断整批电火工品的感度性能,目前还没有成熟的单发电火工品感度性能的预测方法。瞬态脉冲法是一种对电火工品无损检测的方法,通过瞬态脉冲法可得到温升、升温常数、热散失系数及热容等热参数。由热参数预测单发电火工品的感度性能,是一个可取的方案[1-5]。
文献[1]通过试验研究了电火工品的热参数与感度性能之间的关系,指出:温升、升温常数能显著反映电火工品的感度性能,可选用两者之一作为感度性能判断的依据。其不足是无显著性分析过程;分类精度不高;无量化指标,通用性不强。为了充分挖掘试验数据,研究电火工品的热参数与感度性能之间的关系,本文对热参数进行方差分析,然后选取合适的热参数作为特征量,并基于改进的距离判别分析法对电火工品的感度性能进行预测。
1 方差分析
为了定量分析热参数对电火工品感度性能影响的显著性,采用方差分析的方法处理文献[1]的试验结果。假定热参数对感性性能的影响相互独立,运用单因素方差分析法,将试验数据分成两组:发火的电火工品为总体1,试验次数为r1,不发火的电火工品为总体2,试验次数为r2。由每个热参数的数据生成4 个单因素试验数据表,其格式见表1。
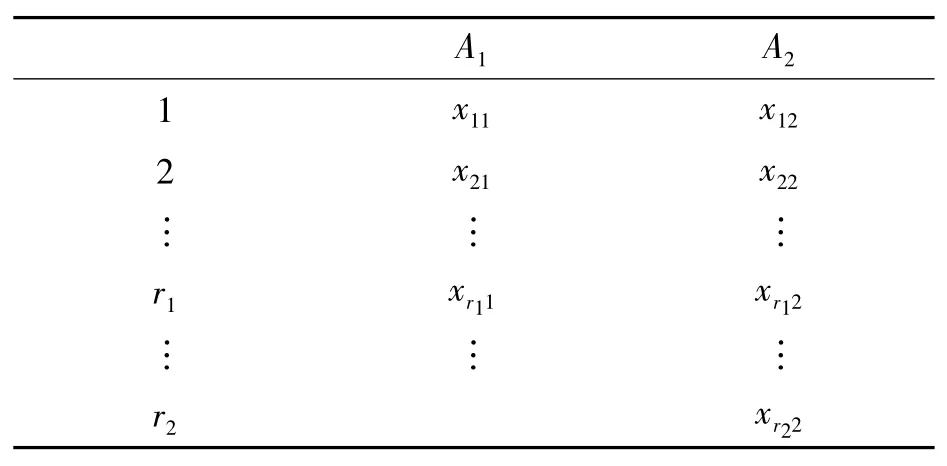
表1 单因素试验数据表
表1 中:A1为总体1(发火)的某一热参数;A2为总体2(不发火)的某一热参数;xij为在第i 个水平(第i 个试验)下第j 个总体的样本。
检验统计量为
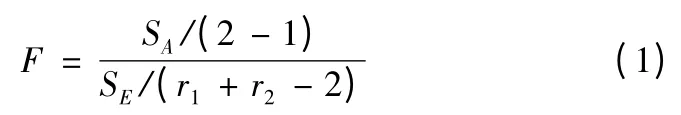
式(1)中:SA为各组数据均值对总方差的偏差平方和;SE为各组内数据对均值偏差平方和的总和。
若两个总体的热参数无显著差异,检验统计量F 服从自由度为n1=2-1,n2=r1+r2-2 的F 分布。为检验差异的显著性,给定显著性水平α,并记F 分布的1-α 分位数为F1-α(n1,n2),若F <F1-α(n1,n2),认为两个总体的热参数无显著差异。
计算出两个总体的温升、升温常数、集总热散失系数及热容无显著差异的概率分别为1.631 9 ×10-8、8.723 5 ×10-5、0.001 7、0.372 1,即在α =0.05 显著性水平下,温升、升温常数及集总热散失系数对电火工品的感度性能影响规律显著。因此,本文选用上述3 个热参数作为电火工品感度性能预测的特征量。
2 预测方法
距离判别分析法是以距离作为相似性度量根据所研究的个体的观测特征量来推断该个体所属类型的一种统计方法。选取合适的相似性度量是距离判别分析的关键。马氏距离不受量纲的影响,避免了多重相关性所造成的信息重叠,是一个有效的相似性度量[6]。标准的马氏距离判别分析法只能进行等级分类,本文对其输出值进行了改进,给出了一个新的感度性能指标。
2.1 标准的马氏距离判别分析法
对于经过瞬态脉冲试验及发火验证试验的电火工品,将其分为两组:发火的电火工品为总体1,不发火的电火工品为总体2。假定两个总体的热参数向量均服从多元正态分布,则待测电火工品与两个总体的马氏距离为[6]

式(2)中:μ1、μ2为总体1 和总体2 的均值向量;Σ1、Σ2为总体1 和总体2 的协方差阵;x 为待预测电火工品的热参数向量;d1(x)、d2(x)为x 与总体1 和总体2 的马氏距离。
若d1<d2则可判定x 属于总体1,即发火;若d1>d2则可判定x 属于总体2,即不发火。
2.2 改进的马氏距离判别分析法
标准的马氏距离判别法只能得出单发电火工品发火或不发火的结论,信息量少,不能进行感度性能排序,不利于质量控制。为了得到单发电火工品感度性能的量化指标,应选择合适的感度性能指标对标准马氏距离判别分析法的输出值进行改进。考虑以下两点:单发电火工品发火的感度性能指标与不发火的感度性能指标的数值之和为1;感度性能指标与马氏距离保持反比关系。即新的感度性能指标满足:

式(3)中:p1(x)为电火工品发火的感度性能指标;p2(x)为电火工品不发火的感度性能指标。本文以单发电火工品发火的感度性能指标作为讨论对象:
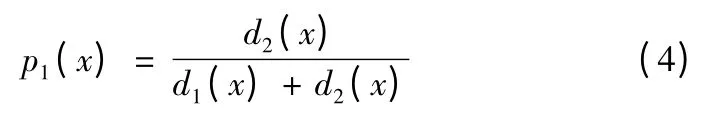
2.3 预测过程
单发电火工品感度性能预测过程:随机选取一定量的电火工品作为学习样本,分别进行瞬态脉冲试验及发火验证试验。将试验过的电火工品按发火与否分成两类,取两类电火工品的温升、升温常数及集总热散失系数作为输入向量,计算两个总体的均值向量、协方差阵。对单发待测的电火工品进行瞬态脉冲试验,由热参数建立新的输入向量,由式(2)、式(4)求出电火工品发火的感度性能指标。
3 实验验证
3.1 数据
3.2 预测
将发火的6 发产品作为总体1,未发火的24 发产品作为总体2,分别计算均值向量μ1和μ2,协方差阵Σ1和Σ2。将第1 发~第30 发产品的热参数分别作为新的输入向量x,预测每发产品发火的感度性能指标,结果见表2 的第5 列。表2 的第1 列为产品的试验序号,各组数据按感度性能指标预测值从大到小降序排列。
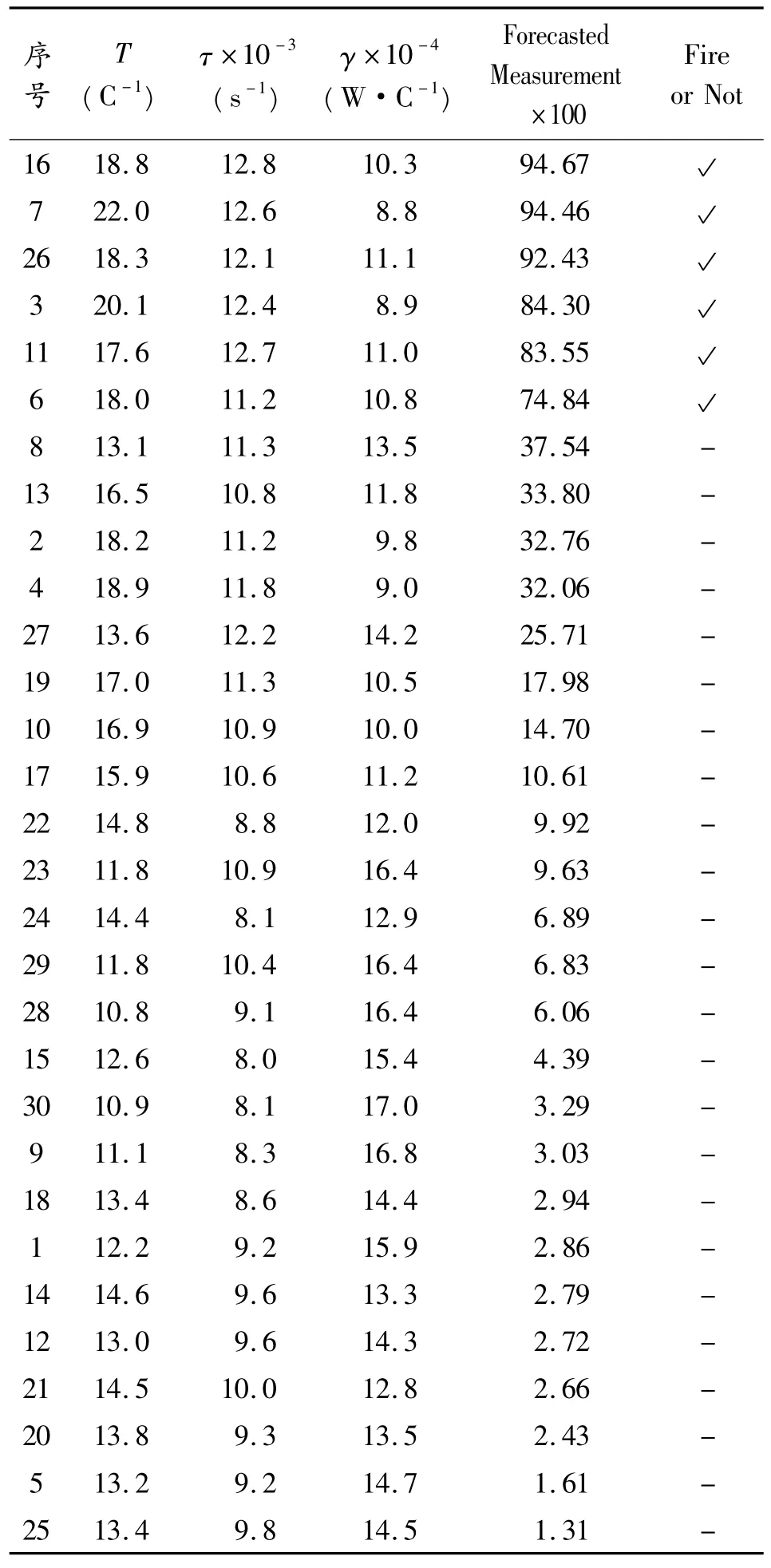
表2 第1 发~第30 发产品的试验结果及预测结果
由表2 可以看出:感度性能指标排在前6 位的产品均发火,感度性能指标排在后23 位的产品均未发火,说明预测结果是可信的。第2 发、第4 发产品温升均排在前6 位,集总热散失系数均排在后6 位,以文献[1]提出的“温升越大,电火工品的感度越高”或“集总热散失系数越小,电火工品的感度越高”作为依据,均会得出感度应排在前6 即发火的结论。但在发火验证试验中两发产品并未发火,产生了误判。本文考虑了第2 发升温常数排在第11 位、第4 发产品升温常数排在第7 位,即升温常数均比较低的事实,融合了3 个热参数的影响,得出两发产品感度低的结论,与实际相符,说明本预测方法克服了以一个热参数作为感度性能的分类依据所造成的精度较低、信息缺失的问题。
需要说明的是:预测方法是基于对试验数据进行方差分析,并采用马氏距离作为相似性度量而得出的,需要有足够多的数据以保证统计学意义。仅从数值来看,感度性能指标预测值大于50%的产品均发火,低于50%的产品均未发火。该指标与产品的发火概率具有一定的类似性,能否认为两者近似?这有待进一步研究。由方差分析的检验统计量可以看出热参数对电火工品感度性能影响的显著性是不一致的,尤其是集总热散失系数对预测的贡献率偏小,为了体现这一点应该在马氏距离的基础上加入特征量的权重[7-10]。本文将3 个特征量同等对待,实际上夸大了集总热散失系数对预测的影响,但由于文献[1]提供的数据偏少,也未造成误判。下一步,应在增加试验次数上的前提下以贡献率为权值重新计算加权马氏距离。
4 结束语
从结果来看,本文给出的感度性能指标能反映电火工品的感度性能,且预测精度高于以一个热参数作为感度分类依据的方法,预测方法是可行的,感度性能指标与概率在数值上相似,具有一定的通用性。可通过以下两个途径进一步提高预测准确度:增加试验次数;研究热参数对感度性能影响的贡献率。
[1]周彬,徐振相,秦志春,等.瞬态脉冲试验中热参数与电火工品发火性能的关系[J]. 火工品,2001,4(4): 32-15.
[2]周彬. 桥丝式电火工品瞬态脉冲无损检测技术研究[D].南京:南京理工大学,2003.
[3]强涛,周彬,秦志春,等.桥丝式电火工品安全电流的预测[J].南京理工大学学报,2006,30(1):110-112.
[4]胡学先.电火工品小电流无损检测的可行性[J].含能材料.2003,11(1):40-42.
[5]胡学先,胡轶. 电火工品的感度控制和预报. 火工品,1999(2):39-42.
[6]袁志发,周静芋. 多元统计分析[M]. 北京: 科学出版社,2002.
[7]Shen Hongbin,Yang Jie,Wang Shitong.Attribute weighted mercer kernel based fuzzy clustering algorithm for general non-spherical datasets[J]. Soft Comput,2006(10): 1061-1073.
[8]蔡静颖,谢福鼎,张永.基于马氏距离特征加权的模糊聚类新算法[J]. 计算机工程与应用,2012,48(5): 198-200.
[9]姚银佩,李夕兵,宫凤强,等.加权距离判别分析法在岩体质量等级分类中的应用[J]. 岩石力学与工程学报,2010,29(2):4119-4123.
[10]赵琳,罗汉,刘京.加权马氏距离判别分析方法及其权值确定——旅游信息服务系统的智能推荐[J].经济数学,2007,24(2):185-188.

