人力资本、全要素生产率与经济增长的相关性——基于中国1952―2004年数据的验证

金银亮

(南京师范大学泰州学院，江苏 泰州 225300)

人力资本、全要素生产率与经济增长的相关性
——基于中国1952―2004年数据的验证

金银亮

(南京师范大学泰州学院，江苏 泰州 225300)

以人均受教育水平代表人力资本，基于中国 1952―2004年的数据，采用向量误差修正模型和 Granger因果检验分析人力资本影响经济增长的一种可能途径：人力资本通过影响全要素生产率进而影响经济增长。结果表明：人力资本与技术进步存在着因果关系，人力资本是全要素生产率的源泉。验证了舒尔茨对“增长余值”的批评；支持了Nelson-Phelps的推论——人力资本并不能简单地等同于一般要素投入；进一步揭示了新古典模型的不足——忽视人力资本对于技术进步的特殊意义，低估了人力资本的贡献。

人力资本；技术进步；全要素生产率；经济增长；Granger因果检验

一、问题的提出

Solow认为经济增长中87.5%份额应归因于“增长余值”，最早对此提出批评的是舒尔茨[1]。舒尔茨认为，所谓“增长余值”是来自精炼化、狭隘化的资本与劳动力的计算方法，没有看到人力资本质量的改进是经济增长的重要源泉[2]。与舒尔茨主要采用语言描述不同，Nelson和 Phelps通过数学模型(NP模型)阐释了人力资本与技术进步，进而与经济增长的关系；他们认为经济的产出增长率取决于经济的创新能力及技术采纳能力，而后者又取决于人力资本存量。NP模型被认为是熊彼特创新增长理论的奠基之一[3]。Mankiw等较早地利用经验数据研究人力资本与经济增长的关系得出，包括人力资本的MRW扩展模型可以解释近80%的跨国收入差距。不过，很多学者对MRW模型提出了质疑[4]。Islam采用面板数据发现，MRW模型所隐含的人力资本与经济增长之间关系并不明确，二者甚至呈负相关[5]。这一发现在Bils 和 Klenow的研究中同样得到证实：尽管有微弱的证据表明人力资本与经济增长之间存在正相关，但是这种关系并不如想像的那样显著[6]。Klenow 和 Rodriguez-Clare则从增长核算的角度对MRW模型提出了批评，人力资本与物质资本实际上仅能解释收入的很小一部分，50%以上的收入差距仍将归因于全要素生产率(以下简称为TFP)[7]。遗憾的是同MRW模型一样，以上批评者们并没有接受NP模型的建议而仍将人力资本视为一种简单的要素投入。

受NP模型的启发，Benhabib和Spiegel的研究不仅否定了MRW扩展模型而且从经验上得到了人力资本影响技术传播速度的证据，支持了熊彼特创新增长理论[8]。之后，Acemoglu以及Aghion 等在关于跨国收入差距的研究中同样发现，不同国家之间的收入差距要归因于人力资本存量差距，因为人力资本存量将决定一个国家的技术创新以及吸收前沿技术的能力[9,10]。

人力资本与经济增长的关系也受到了中国众多学者的关注，但在人力资本度量以及结论方面存在很大差异。沈坤荣和蔡昉等分别选用在校大学生数与识字率作为替代变量得出人力资本与经济增长显著正相关[11,12]。林毅夫、刘培林采用具有小学文化程度的人口占总人口的比例作为替代变量得出人力资本对经济增长作用并不明显[13]；胡永远采用同样的指标发现虽然人力资本对经济增长的贡献率显著为正，但其贡献率较小且并不具有长期产出增长效应[14]。从国内已有文献来看，大多研究并不在于探究人力资本是如何影响经济增长的。

鉴于传统模型将人力资本简单设定为一般意义上的要素投入，得出人力资本对于经济增长贡献的结论不一致，笔者拟运用基于向量误差修正(Vector Error Correction, VEC)模型的Granger因果检验分析人力资本影响经济增长的一种可能途径：人力资本通过影响全要素生产率(TFP)进而影响经济增长。如果这一假定成立，那么新古典框架将人力资本等同于一般意义上的要素投入必然导致对人力资本贡献的低估。

二、VEC模型与数据来源

1．VEC模型

一般地，向量自回归 (Vector AutoRegression，VAR)模型可以忽略具体理论来研究人力资本要素与经济增长之间的动态关系，但是该模型对数据平稳性要求较高；如果变量非平稳，可以进行协整检验，如果变量之间存在协整关系，则可以通过建立约束下的VAR模型，即向量误差修正（VEC）模型来进行回归分析，一般形式如下所示：

以下为滞后2期的多变量向量误差修正模型：

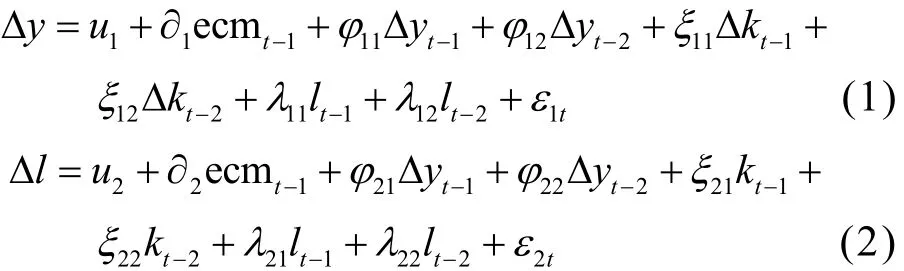
本文构建包括人力资本的增长模型形式为：

式中Y、K、H和L分别表示t时期的总产出、总物质资本存量、人力资本存量以及简单劳动投入，ε为误差项，α、β和γ分别为相应要素的投入产出弹性。At表示t时期的全要素生产率，并假定年均呈指数增长，即根据定义可知，

时间t的系数ω即为第t年全要素生产率的增长率；它表明在保持其他要素投入不变的情况下，产出相对于时间的即时百分比变化率。假定

这一处理反映每一年的知识累积效应对人力资本积累的贡献是不同的。其中表示第t年劳动力平均受教育年限，为的分段折算函数，反映单位劳动受教育的效率，即为明塞回归系数。由于中国尚未提供公认的教育回报率数据，本文参考张帆等人[15]的研究，采用Psacharopoulos 和Anthony已经测算的数据，教育年限小于6年时回报率为0.18，6～12年之间为0.134，大于12年时为0.151。此外假定不接受任何教育的劳动力只提供1单位简单劳动，即 (0)0U = 。同时定义第t年的全要素生产率为：

也有学者采用另外一种设定形式：

2．数据说明与处理

(1) 人力资本估算。由于统计资料的限制，中国至今没有完整的受教育年限数据。已有研究文献通常采用各级教育的人口比例、在校大学生数、识字率或者教育经费支出来替代人力资本。不过这些替代变量均存在不足，而较为合适的替代变量是人均受教育年限[16]。Holz提供了中国1978―2004年的人均受教育水平[17]，而 Wang和 Yao则提供了1952―1999年的人均受教育年限数据[18]。由于估算方法不同，这两份数据的口径并不一致。其中Holz提供的数据与陈钊等估算的 1987―2001年的数据基本一致，而Wang和Yao的估计要比其他两份数据小许多。因此，本文 1978―2004年的数据直接取自Holz，1952―1977年的数据则是根据Holz与 Wang和Yao的数据按照时间趋势作线性回归，利用回归模型对人力资本进行估算。

(2) 物质资本存量的估算。Chow以及张军等对中国历年物质资本存量的估计最有代表性。不过由于在当期投资选择上的不同，这两篇文献所估算的历年物质资本存量有很大出入。Chow提供了1952―1998年的物质资本存量的估算结果，张军提供了物质资本存量的详细估算方法但没有提供完整的估算结果[19,20]。为节省篇幅本文只报告了根据Chow的回归结果。因此，本文1952―1998年的物质资本存量数据直接来自Chow等，而1998年后的缺失数据则按照趋势外推法进行估算。

三、回归结果与要素贡献分析

由于 1978年以前技术进步不明显，因此，本文设定1978年以前的时间t取值为0，1978年以后的时间t依次取值为1，2，…。单位根检验表明，人力资本、物质资本、劳动以及产出水平均为一阶差分平稳序列，因此，只要回归结果的残差拒绝存在单位根就可以确认这些变量之间存在协整关系。对回归结果残差的单位根检验结果如表 1中 ADF行所示，所有模型均拒绝存在单位根的原假设。

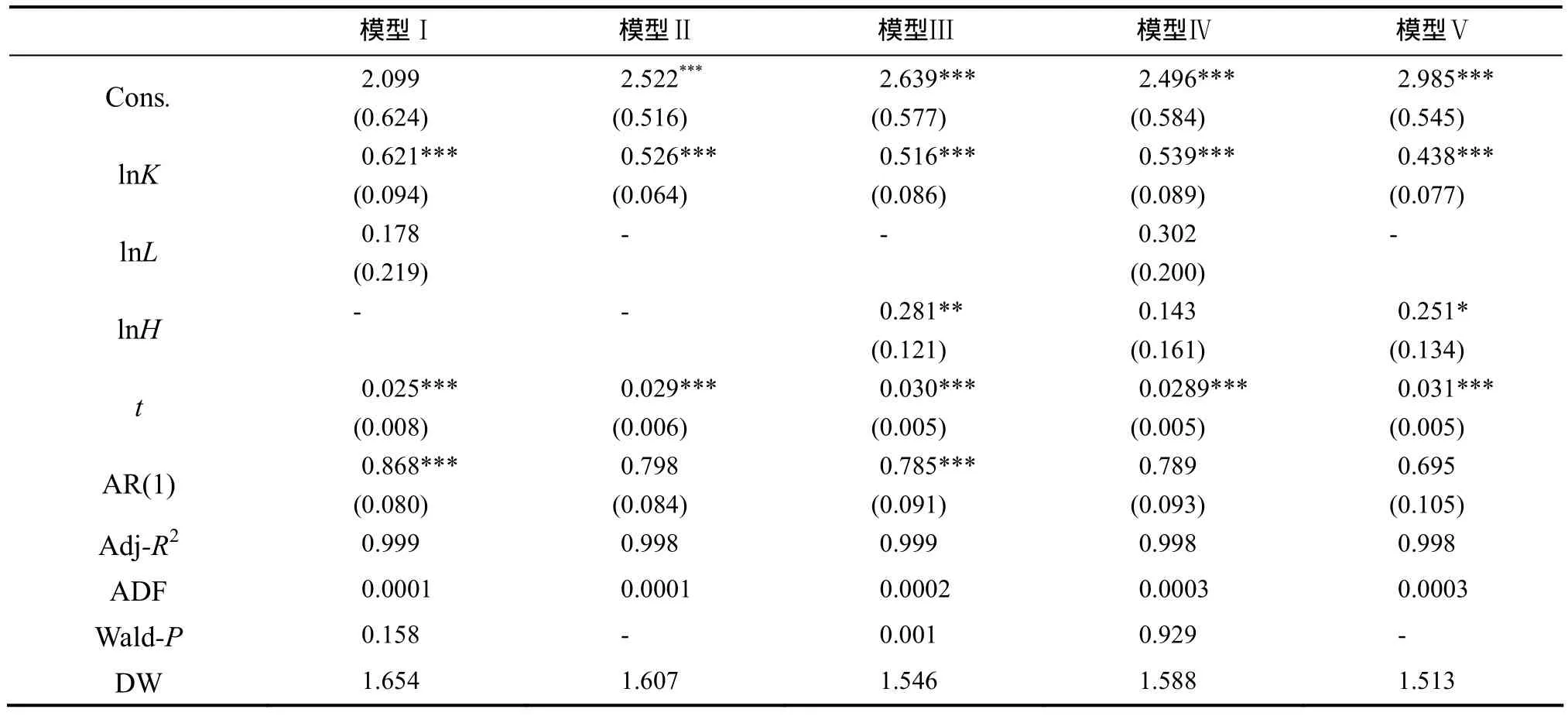
表1 回归结果(1952―2004年，Obs.=53)

1．生产函数的估计

模型Ⅰ报告的是参数无任何约束的回归结果，时间t的系数为0.025并且在1%的水平上通过检验，这表明1978―2010年平均技术进步率约为2.5%。物质资本的投入产出弹性为0.621，简单劳动的投入产出弹性为0.178。前者在1%的水平上通过显著性检验。直观上，资本弹性与劳动弹性系数之和小于 1似乎表明存在规模报酬递减，不过Wald检验表明在统计意义上并不能拒绝规模报酬不变。模型Ⅱ是在规模报酬不变前提下的回归结果。相比于模型Ⅰ，模型Ⅱ中物质资本的投入产出弹性下降为 0.526并且在 1%的水平上通过检验；技术进步率则上升为0.029且同样在1%的水平上显著。模型Ⅲ是引入了复杂劳动要素的回归结果。由于Wald检验拒绝了规模报酬不变的假设，因此模型Ⅲ报告的是参数无任何约束的回归结果。其中复杂劳动的弹性系数为0.281并且在5%的水平上显著；由于考虑了劳动力的平均受教育年限，物质资本的弹性系数比模型Ⅰ的估计结果小些，不过仍在合理范围内。模型Ⅳ是直接将平均受教育年限作为一种要素投入并且假定参数无任何约束的回归结果。由于简单劳动要素以及复杂劳动要素的检验都不显著。因此模型Ⅳ的回归结果不是很好。由于Wald检验不能拒绝三个要素弹性之和为1的假设，模型Ⅴ报告了模型Ⅳ在规模报酬不变情况下的回归结果。由于教育年限的引入，物质资本的弹性系数下降为 0.438，相比于前面几个模型有很大区别。人力资本弹性系数为0.251且在 10%的水平上显著，这一结果与胡永远的估计基本一致[14]。技术进步率为 0.031，小于Chow估计的0.287，不过Chow在回归分析中并未考虑人力资本变量[19]。总的来说，可以断定人力资本与经济增长之间存在显著的正相关性。

2.要素贡献分析

表2分析了以平均受教育年限单独作为要素投入的各要素对经济增长的贡献，结构参数来自模型Ⅴ的估计结果。从1978―1992年以及1992―2004年这两个时间段的数据来看，简单劳动的贡献呈下降趋势(由第一时期的 12.12%降至第二时期的3.96%)，这说明无人力资本投资的简单劳动对经济增长的作用越来越不重要。物质资本的贡献比重由第一时期的39.34%上升至第二时期的55.66%，这说明中国经济发展过程中存在着资本投资过度的可能。与此形成鲜明对比的是人力资本贡献，尽管由第一时期的2.84%上升至第二时期的3.31%，但无论是在存量上还是在增量上其对经济增长的作用远比不上物质资本。就整个时期来看，TFP的平均贡献比例为36.56%。

表2 以平均教育年限单独作为劳动投入的各要素贡献

表 3分析了以复杂劳动作为人力资本投入的各要素对经济增长的贡献，结构参数来自模型Ⅲ。1952―2004年复杂劳动要素对经济增长的贡献为16.8%，比采用平均受教育年限要高些，但远低于同时期物质资本约 57.76%的经济增长贡献。综合表2、表3可以发现，尽管人力资本变量对产出增长的贡献率为正，但无论是采用复杂劳动还是平均教育年限，人力资本对产出增长的贡献率都很低。相比于微观经验所证实的教育水平对收入的巨大影响，宏观经验结论却非常不一致。不过据此判断人力资本不重要可能过于仓促，问题在于人力资本能否等同于一般意义上的要素投入呢？

表3 以复杂劳动作为人力资本投入的各要素贡献

四、Granger因果检验

从表2和表3可以看出，TFP对经济增长平均贡献近40%的增长份额，比较而言人力资本的贡献非常低。那么导致TFP上升的原因是什么呢？人力资本能构成全要素生产率上升的原因吗？如果回答是肯定的，那么传统的经济增长模型设定显然低估了人力资本对经济增长的贡献。在统计学上确定一个变量的变化是否为另一个变量变化原因的方法是Granger因果检验。Granger因果检验的思路在于：如果X是引起Y变化的原因，那么在Y的过去值的回归中添加X的过去值作为独立变量应当会显著地增加回归的解释能力。以时间序列数据为依据的实证分析必须满足平稳性设定，否则会产生谬误回归问题。因此，笔者拟根据模型Ⅳ中的估算数据进行分析。为了同时保证数据的连续性以及必要的数据长度，笔者放弃了 1974年以前的时间序列数据。人力资本与全要素生产率水平值(1974―2004 年)的单位根检验结果表明，二者均不能拒绝存在单位根，进一步检验显示人力资本与全要素生产率的一阶差分平稳(表4)。

由于人力资本与全要素生产率均为 I(1)序列，笔者进一步采用 EG两阶段法对二者进行协整检验。人力资本与全要素生产率之间的 OLS估计为TFP=1.654+1.008H，所有的系数均在 1%的显著性水平上通过检验，式子残差的ADF统计量为-4.22，P分位数为0.01，因此可以拒绝残差存在单位根的原假设，这说明二者之间存在长期的稳定关系，对二者进行回归不致产生偏误。如果两个变量均为一阶单整并且相互间存在协整关系，那么可以确定二者之间一定有某种因果关系[21,22]，但协整只表示变量间有长期关系而不能显示短期关系，同时考察长期影响与短期影响的办法是加入误差修正项。本文含误差修正项的模型为：

就本文来说，Granger因果检验具体规则为：如果ρ显著并且γ的联合检验不显著，则认为人力资本在长期内对TFP具有领先关系，或者说人力资本是TFP的Granger意义上的原因；如果至少某一个λ的估计系数显著，则认为人力资本变化在短期内对TFP具有领先关系；如果ρ、λ的估计系数都显著并且γ的联合检验不显著，则表示人力资本对TFP同时存在长期和短期的领先关系。

由于 Granger领先检验对滞后期的选择十分敏感，滞后期过多会影响自由度，而过少则可能导致自相关等误差。笔者选择较大的6期作为基准，此时各种判别规则一致显示最优滞后为2期(表5)。因此VEC模型将选择2期滞后。

表5 VEC模型滞后选择标准

利用ECTt-1=TFPt-1-1.654-1.008Ht-1，将误差修正项代入(4)式后的回归结果如表 6所示。尽管DTFP(-1)的系数在5%的水平上显著，但DTFP(-1) 与DTFP(-2)的联合检验显著性水平达到12%，无法拒绝二者影响为零的原假设。因此可以认为 DTFP的滞后项对当前无影响。误差修正项的系数为-0.16，P值为7%，在10%的水平上显著，这说明从长期看人力资本对TFP会有显著性影响。负号同时也表明系统可以对偏离进行调整。比如若前1期ECT偏离1单位，那么本期系统将会使这种偏离下降0.16。从短期看人力资本并不会对技术进步产生影响，体现在DH的2期滞后的系数均不能通过T检验。因此，从长期看人力资本将构成全要素生产率进而技术进步的原因，尽管在短期内这种作用不太明显。结果表明，简单地将人力资本视为一般意义上的要素投入实际上低估了人力资本对经济增长的贡献。

表6 Granger因果检验(1974―2004年)

五、结论

上述研究采用基于VEC模型的Granger因果检验方法揭示“增长余值”的内涵在于劳动力素质的显著提高，验证了舒尔茨对“增长余值”的批评。研究结果同样支持 Nelson-Phelps的推论：人力资本并不能简单地等同于一般要素投入。研究结果进一步证明人力资本是TFP的源泉，揭示了新古典模型对待人力资本的不足：由于忽视了人力资本对于技术进步的特殊意义从而在很大程度上低估了人力资本本来的贡献。

[1] Solow R．Technical change and the aggregate production function[J]．Review of Economics and Statistics，1957，39(1)：312-320．

[2] 舒尔茨．人力资本投资[M]．北京：北京经济学院出版社，1999．

[3] Nelson R，Phelps E．Investment in humans，technological diffusion，and economic growth[J]．American Economic Review：Papers and Proceedings，1966，51(2)：69-75．

[4] Mankiw N G，David Romer，David Weil．A contribution to the empirics of economic growth[J]．The Quarterly Journal of Economics，1992，107(2)：407-438．

[5] Islam N．Growth Empirics：A panel data approach[J]. The Quarterly Journal of Economics，1998，113(1)：325-329．

[6] Bils Mark，Klenow Peter J．Does schooling cause growth[J]．American Economic Review，2000，90(5)：1161-1183．

[7] Klenow Peter，Andres Rodriguez-Clare．The neoclassical revival in growth economics：Has it gone too far? [R]．NBER Working Paper，1997：73-103．

[8] Benhabib Jess，Spiegel Mark M．The role of human capital in economic development：evidence from aggregate cross-country data[J]．Journal of Monetary Economics，1994，34(2)：143-74．

[9] Acemoglu，Aghion and Zilibotti．Distance to frontier selection and economic growth[R]．NBER Working Paper，2002．

[10] Aghion P，P Howitt，G L Violante．General purpose technology and wage inequality[J]．Journal of Economic Growth，2002，7(4)：315-45．

[11] 沈坤荣，马俊．中国经济增长的俱乐部收敛特征及其成因研究[J]．经济研究，2002(1)：33-39．

[12] 蔡昉，都阳．中国地区经济增长的趋同与差异——对西部开发战略的启示[J]．经济研究，2000(10)：30-37．[13] 林毅夫，刘培林．中国的经济发展战略与地区收入差距[J]．经济研究，2003(3)：19-25．

[14] 胡永远．人力资本与经济增长——一个实证分析[J]．经济科学，2003(1)：54-60．

[15] 张帆．中国的物质资本与人力资本估算[J]．经济研究，2000(8)：19-25．

[16] 陈钊，陆铭，金煜．中国人力资本和教育发展的区域差异——对于面板数据的估算[J]．世界经济，2004(12)：25-31．

[17] Holz Carsten A．China’s economic growth 1978-2025：what we know today about China’s economic growth tomorrow[R]．Hong Kong University of Science & Technology Working Paper，2005．

[18] Wang Yan，Yao Yudong．Sources of China’s economic growth 1952―1999： Incorporating human capital accumulation[J]．China Economic Review，2005，14(1)：32-52．

[19] Chow G C，Lin An-loh．Accounting for economic growth in Taiwan and mainland China：A comparative analysis [J]．Journal of Comparative Economics，2002，30(4)：507-530．

[20] 张军，吴桂英，张吉鹏．中国省际物质资本存量的估算——1952―2000[J]．经济研究，2004(10)：35-44．

[21] 古扎拉蒂．计量经济学基础[M]．北京：中国人民出版社，2004．

[22] Gujarati D．Basic Econometrics (4TH)[M]. New York：McGraw-Hill，2003：87-98．

责任编辑：李东辉

Relationship between human capital ,total factor productivity and economic growth: Verification based on the data from 1952-2004 of China

JIN Yin-liang
(Taizhou College, Nanjing Normal University, Taizhou 225300, China)

Based on the data of 1952-2004 in China, this paper made per capita educational level to define human capital, and adopted VEC and causality stat. to analyze a potential method that human capital could influence the economic growth. This paper illuminated a possible way that through affecting the TFP, human capital would further influence the economic growth. The results showed that causal relation did exist between HR and the technical progress. Human capital was the origin of TFP, which verified Schultz’s criticism to “growth remaining value”, and supported Nelson-Phelps’ deduction that human capital could not easily equal to “general input”。Besides, the results further indicated the weakness of “new classical model”, which ignored the special significance that human capital could affect technical progress and underestimate the contribution of human capital.

human capital; technological advances; TFP; economic growth; Granger causality stat

F124.7

A

1009-2013(2014)02-0058-06

10.13331/j.cnki.jhau(ss).2014.02.010

2014－02－17

南京师范大学泰州学院基金项目(Q201205)

金银亮(1980—)，男，江苏邳州人，硕士、讲师，研究方向：人力资本测算。