渐进式异源光学卫星影像SIFT匹配方法
戴激光,宋伟东,李 玉
辽宁工程技术大学测绘与地理科学学院,辽宁阜新 123000
渐进式异源光学卫星影像SIFT匹配方法
戴激光,宋伟东,李 玉
辽宁工程技术大学测绘与地理科学学院,辽宁阜新 123000
针对异源光学卫星影像SIFT算法匹配率低的问题,基于SIFT匹配方法,以特征点相对主方向、相对尺度为约束条件提取初始匹配点,并利用初始匹配点构建Delaunay三角网,采用点扩散方式来获取局部几何约束模型,基于特征点主方向约束、特征向量欧氏距离及局部RANSAC误差剔除方法,渐进式地实现了对异源光学卫星影像的高精度匹配。与其他匹配算法对比试验结果表明,在异源影像存在较大尺度、旋转差异的情况下,本文算法具有匹配数量大、精度高的优势。
渐进式;异源影像;SIFT;匹配;点扩散
1 引 言
异源影像间由于存在成像机理、尺度、时相等差异,使得其匹配问题长期以来一直未能得到很好的解决[1-2]。SIFT算法[3]具备较好的抗尺度、旋转及光照变换能力,在影像匹配中得到了广泛的应用。例如文献[4]采用SIFT算法对同源光学影像进行了匹配,取得了较好的试验结果。但作为一种局部描述子,当影像中存在重复或相似场景(城市中相似的楼房与道路及山区中的梯田等地物)时,以特征向量距离为相似性测度将会降低匹配的成功率[5]。因此需要选取恰当的几何约束方式来限定特征点匹配范围,以此来降低相似地物对于匹配的影响。针对这一问题,一种匹配策略是直接对特征点进行几何约束,例如文献[6]通过提取特征点异源核线,限定了特征点匹配的范围,提高了匹配的成功率。文献[7]通过对影像进行粗校正,采用改进主方向的SIFT算子匹配光学和SAR影像。文献[8]对SIFT算子中的尺度和方向进行约束,克服了不同影像间由于梯度和方向所引起的误差。文献[9]改进SFIT特征提取方式,通过特征点角度、尺度约束实现了对异源影像的匹配。文献[10]提出了一种顾及影像几何特征的角点特征提取算法,以经过该点的线数目及线之间的夹角作为描述子对不同光学影像进行了匹配。
另外一种匹配策略是基于可靠的初始匹配结果,采用动态传播几何约束的方式来渐进式获取更多的匹配点。如文献[11]利用初始匹配点构建三角网,以此来动态细化获取更多的匹配点,但问题在于匹配结果依赖初始同名点的分布,并且其特征匹配测度很难适用于不同分辨率的影像。文献[12]在此基础上进一步引入了梯度方向限制及仿射不变标准互相关测度,但仍然无法解决对于初始匹配点分布上的依赖。文献[13—15]也采用SIFT初始匹配点进行影像粗变换分析,利用分析结果及特征点尺度等特征对未匹配特征点进行相似性判断迭代匹配传播获取更多同名点集,但该方法中的测度函数很难适用于不同分辨率的卫星影像。
相对而言,第2种匹配策略匹配点数量更多,精度更高。因此本文基于第2种匹配策略,以异源光学卫星影像为研究目标,提出一种基于SIFT特征的渐进式匹配算法。算法首先利用SIFT匹配算法和角度、尺度约束模型获取初始匹配点,并基于随机抽样几何模型(random sample consensus,RANSAC)剔除误匹配。接着基于初始匹配点构建三角网,通过点扩散方法建立局部几何约束模型,实现对待匹配影像上所有特征点的约束匹配。
2 特征提取
由于受到传感器观测角度、时相、尺度不一致等因素影响,异源影像对地物目标的刻画往往存在一些差异,这使得角点、拐点、极值点等特征在匹配中受到限制,而SIFT算法能够在一些影像灰度渐变区域获得稳定的特征点,更加适宜于异源影像的匹配[12]。SIFT算法通过构建影像尺度空间的方式寻找对尺度、旋转、光照变换保持不变的兴趣点,并利用梯度方向向量来对特征点进行描述,其步骤包括:尺度空间构建、特征点主方向确定、描述符生成及特征匹配4个步骤[3]。根据SIFT原理,特征点表达为f=(x,σ,θ,d),其中,x表示为特征点坐标;σ表示为平滑尺度因子;θ表示为特征点主方向;d表示为SIFT特征描述符。
3 特征匹配
渐进特征匹配方法包括初始匹配和渐进式几何约束匹配两个阶段。
3.1 初始匹配阶段
假定fi和分别为参考影像上和待匹配影像上的特征点,定义特征点之间的相对尺度δσ=相对主方向δθ=θi-其具体匹配步骤如下:
(1)依次计算匹配点对描述子之间的欧氏距离,将最近邻与次近邻比值小于阈值ratio设定为候选匹配点,同时记录匹配点对之间的相对尺度δσ和相对主方向δθ。
(2)随机抽取3对匹配点。两两判断相对尺度之差和相对主方向之差是否低于阈值h1,满足要求则直接进入(3),否则重新抽取3对匹配点。
(3)利用3对匹配点构建影像仿射转换模型,基于该模型对候选匹配点进行分析,当距离低于h2时,保留该匹配点,否则该匹配点被剔除。
(4)采用基于单应矩阵的RANSAC算法对匹配点进行误差剔除,获取最终的初始匹配点集。
3.2 渐进式匹配阶段
作为计算几何中非常重要的概念,Delaunay三角网在遥感影像局部纠正中起到关键的作用[16]。本文首先利用初始匹配点Delaunay三角网构建几何约束模型。假设f={fi|i=1,2, …,n},f′={|j=1,2,…,m}分别为参考影像和待匹配影像上的三角网内对应特征点。依据摄影测量与遥感及计算机视觉理论,如果点fi与是一对同名点,根据局部连续性约束,fi的变形参数要受到3个顶点的影响[17-18]。同样在三角网外影像特征点要受到邻域像素变形因素的影响。因此本文首先建立针对特征点的局部几何约束模型,在此基础上对特征点进行约束匹配。
3.2.1 局部几何约束模型的构建
依据小面元原理,三角网影像范围内的特征点利用3个顶点构建仿射模型,均可将其作为该点的局部几何约束模型。而对于不在三角网范围内的特征点,无法直接获得局部几何约束模型。针对这一问题,根据Voronoi剖分理论,本文提出了一种点扩散的方法。
如图1所示,O为影像中心点(初始匹配点的重心),R为点扩散半径,F为扩散区,红色直线为三角网。随着R值的扩大,以O为中心点,F形成3×3、5×5、7×7、…、m×n影像矩阵,逐渐覆盖整幅影像,以此方式通过逐层对边缘点分析来获取整幅影像像素点的几何约束模型。
如图1所示,其中K1和K2分别为在扩散半径为R时两种不同的边缘点,通过对局部放大图进行分析:
(1)K1点与影像三角网不相邻,但由于本文采用的是点扩散方法,在其八邻域内必有已获得局部几何约束模型的点。寻找邻域内已获取局部几何约束模型的点,将其参数赋予该点。如果出现多点几何约束模型不同,则将多点几何约束模型参数平均后赋予K1点,以此避免对单一约束模型的依赖。
(2)K2为临近影像三角网边缘点,因此在其八邻域中必有一点在三角网内或几个点在三角网内。出现前者情况时,将该点的几何约束模型直接赋予K2点。当出现后者情况时,寻找最多同一几何约束模型点的参数模型,将该模型参数赋予K2点。
3.2.2 约束窗口下提取匹配点
本文对待匹配影像构建局部几何约束模型后,建立针对特征点的约束窗口,在该窗口中利用特征点的主方向约束、特征向量信息进行匹配。
如图2所示,其中,点PTsrc为待匹配点;红色交叉点PTthe为利用局部几何约束模型计算得到的理论匹配点;dr为约束窗口半径,窗口内黑点为特征点,箭头方向为特征点主方向。首先计算待匹配点与窗口内特征点的相对主方向,通过与初始匹配中记录的相对主方向δθ差值,判断是否符合阈值h1,符合要求方可作为候选匹配点,其次通过计算其特征向量欧氏距离的方法来提取同名点。本文利用统计特征点的最近次近距离来进行同名点的提取。通过对比分析,比值设定为0.5。
3.3 误差剔除模型
上述初始匹配策略仅能得到初始同名点,匹配精度较低,需要进行初始同名点的粗差剔除。通常情况下,粗差剔除方法常选用RANSAC算法,利用RANSAC算法优化仿射不变特征匹配,当样本中存在50%以上的误匹配时,依然可以有效获取正确的匹配[19-20]。但本文通过多组试验发现RANSAC算法受到同名点空间分布密度的制约。其原因在于RANSAC在构建几何转换模型时,以适应该模型同名点的数量作为模型构建的判断标准。这使得同名点密集区域构建的转换模型权重必然较大,该区域同名点得以最大程度保留下来,反之同名点稀疏区域由于权重较小,不能适应RANSAC算法所构建的单应矩阵而被误认为是伪同名点被剔除掉。
针对存在的问题,为提高同名点对的匹配精度,本文采用一种从整体到局部分步式的RANSAC误差剔除方法。核心思想是:首先进行一次全局式的RANSAC处理,设定较高的阈值δ1,其目的是避免不同局部区域间几何转换参数差异过大;其次在不同区域内进行RANSAC粗差剔除,设定较小的阈值δ2,目的是为了提高局部区域内同名点的精确度。这种算法不仅保证了大范围上同名点的精度,同时保证位于同名点稀少区域的控制点不被剔除。
4 试验与分析
4.1 试验数据及评价标准
选取如图3所示3组测试数据进行算法测试。图3中每组影像((a)—(c))中按照从左到右顺序的第1幅为参考影像,第2幅为待匹配影像,相关数据描述见表1。由于所选取的影像像对覆盖区域地形复杂,不同同名点之间变形参数不一致,不能简单地通过构建如仿射、多项式、单应矩阵等模型检测同名点精度,因此本文首先在ENVI软件中利用人工来对影像均匀选取20对测试点,然后根据匹配结果利用小面元微分法对影像纠正计算测试点坐标,最后按照式(1)来计算匹配精度
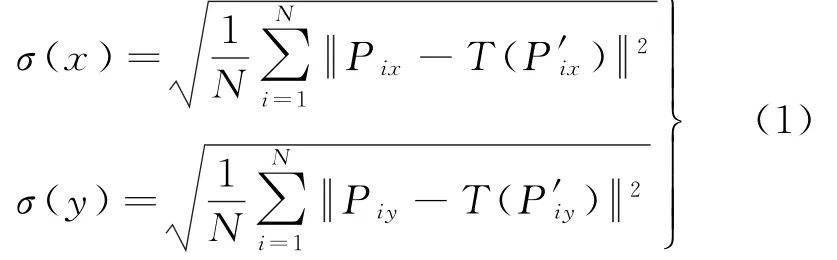
式中,σ(x)、σ(y)为分别为x、y方向误差;N为检测点数量;Pix、Piy为人工实测点x、y方向坐标;T (Pix′)、T(Piy′)为解算出来点x、y方向坐标。

表1 测试数据描述Tab.1 Description of the test data
4.2 试验参数分析
由于本文算法在不同处理阶段均涉及参数的设定问题,因此需要对这些参数进行分析。
4.2.1 初始匹配阶段参数设定
4.2.1.1 阈值h1设定
`在初始匹配阶段,阈值h1主要作用是提取3对精确匹配点,并以此来建立影像仿射转换模型匹配后续同名点,因此其精度要求较高。如表2所示,本文对阈值h1值为0.01~0.1时的匹配结果进行分析。其中,σ(x/y)表示同名点在像方x向和y向的误差,单位为像素。

表2 h1值对匹配结果的影响Tab.2 Impact on matching result due to h1value
如表2所示,阈值h1变化对精度、时间影响较小。故从匹配数量的角度考虑,设定h1值为0.1。
4.2.1.2 阈值h2设定
阈值h2是对初始匹配阶段全局性影像仿射转换模型的精度分析,由于异源影像存在局部变形,并且后续匹配过程中采用RANSAC算法进行误差剔除,因此其精度要求较低,故论文仅对阈值h2为10~20之间的匹配结果进行分析。
如表3所示,匹配点提取时间和精度相差不大,依据匹配数量结果,本文设定h2值为15。
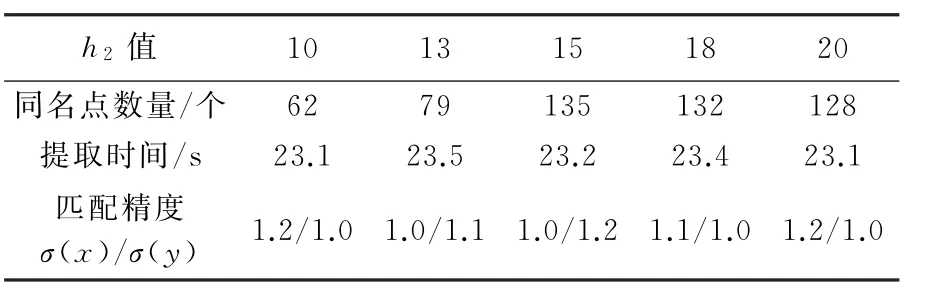
表3 h2值对匹配结果的影响Tab.3 Impact on matching result due to h2value
4.2.2 渐进式匹配阶段参数设定
在渐进式匹配阶段,窗口半径dr值过大固然可以避免误匹配点的引入,但也加大了匹配的复杂度。反之较小则有可能导致误匹配问题的出现。
4.2.2.1 点PTsrc在三角网内dr的设定
由于点PTsrc位于影像三角网范围内,距同名点较近。一般来说,距同名点越近,其局部几何约束模型参数精度越高。因此对于dr的设定不宜过大,本文分别对dr值为1~10之间进行匹配结果对比。
通过表4对dr的统计分析发现,随着dr值的增大,提取同名点时间在不断扩大,这符合随着dr的增大,约束窗口扩大使得特征点增多,加大计算复杂度的规律。综合同名点精度和数量来看,在dr值为3时算法具有较高的匹配率与匹配精度。虽然dr值低于3时,同名点提取匹配数量较高,但存在精度差的问题。因此本文设定dr值为3。

表4 dr值对匹配结果的影响Tab.4 Impact on matching result due to drvalue
4.2.2.2 点PTsrc不在三角网内dr的设定
由于点PTsrc不在影像三角网范围内,其局部几何约束模型是利用中心点蔓延来构建的,其几何约束模型精度必定较低。在这种情况下,对dr的设定数值不宜太小,因此论文分别对dr为 6~15之间进行匹配点数量和精度对比分析。
由表5可以看到,随着dr的增大,同名点提取时间不断扩大。对比同名点精度和提取数量,本文设定dr值为6。

表5 dr值对匹配结果的影响Tab.5 Impact on matching result due to drvalue
4.2.3 粗差剔除阶段参数设定
4.2.3.1 阈值δ1的分析
阈值δ1适用于全局影像上的同名点几何约束,取值不宜过小。故本文对δ1值在0.01~0.1之间同名点提取的数量和精度进行分析。
从表6可以观察到,随着δ1值变大同名点数量也在逐渐增多,这表明约束条件的降低能够获取更多的同名点,但同时匹配精度也在下降。因此从同名点的数量和精度综合考虑,设定δ1值为0.03。

表6 阈值δ1对同名点的影响Tab.6 Control Point due to thresholdδ1
4.2.3.2 阈值δ2的分析
阈值δ2的设定是为了提高在局部区域影像上同名点的精度,故阈值δ2的设定不宜过大。本文对δ2值在0.000 5~0.005之间同名点提取的数量和精度进行分析。
从表7可以观察到,δ2值与δ1值对同名点的数量和精度影响趋势近似,故本文设定δ2值为0.001。

表7 阈值δ2对同名点的影响Tab.7 Control Point due to thresholdδ2
4.3 试验结果与分析
本文中在初始匹配过程中,为避免正确点被过滤掉,根据文献[3]的建议设定ratio为0.8。其中试验环境:操作系统为Windows7,CPU的主频为2.93 GHz,试验软件为vc6.0。
图3给出了3对测试数据的匹配及纠正结果。其中红色点为初始匹配结果,蓝线为三角网连线,绿色点为渐进式匹配获取的结果,最终匹配点结果为红色点与绿色点匹配数量总和,每组影像((a)—(c))中按照从左到右顺序的第3幅为小面元纠正结果。表8给出了本文算法与经典SIFT算法和文献[9]匹配方法基于小面元纠正模型的纠正结果。其中,表中匹配点表示剔除粗差后剩余的正确匹配点,计算时间以秒为单位。

表8 不同算法的匹配性能对比Tab.8 Comparison of matching performance of different algorithms
对表8结果分析后表明:
(1)本文方法的匹配精度均高于其他方法。但同时可以看到本文算法计算时间更长,考虑到匹配点和时间的对比,表明本文所提算法具有更高的效率。
(2)对3组数据的测试结果表明,在高分辨率影像中测试数据精度较低,这表明在同样的变形情况下,高分辨率使得影像变形细节被放大,进而导致匹配精度下降;同样对(b)和(c)对比可以看到,虽然(c)相对于(b)存在较大的旋转变形,但由于(b)覆盖区域地形更加复杂,地面起伏更加剧烈,这使得匹配精度进一步下降。
(3)通过对3组数据匹配点数量对比分析,本文所提算法的匹配数量是SIFT算法的近8倍,这验证了SIFT算法通过特征向量作为匹配测度匹配率低的论断,而文献[9]的算法虽然有初始的粗匹配引导,但由于粗匹配精度太低使得匹配结果仍然不能令人满意。而本文算法由于采用了初始匹配点建立Delaunay三角网作为几何约束模型的基础,通过点位扩展的方式提高了特征点几何约束的能力,较大程度上避免了由于相似地物造成的误匹配现象,大幅度提高了影像匹配的能力。
(4)从匹配点的影像分布可以看到,本文方法在3组影像的渐进匹配点均弥补了起始匹配点分布上的不合理性,使得同名点的分布更趋于均匀,验证了本文所提算法的稳定性。
综合上述分析,以数据采集区域为地形复杂的山区、城区,存在不同局部变形幅度的3对异源卫星影像为研究对象,通过与经典SIFT算法和文献[9]算法的匹配结果比较表明,本文算法在同名点数量、精度、分布合理性及匹配效率上均表现出一定的优势,从而有效地证明本文算法具有良好的稳健性。
5 结 论
本文基于SIFT特征点,提出了一种渐进式的SIFT匹配方法,试验结果表明可以较好地适用异源影像的匹配任务。但由于本文算法在运行过程中需要建立局部几何约束模型,因此本文算法计算量较大,运算时间偏长。后续的研究应该是如何提高算法的计算速度,以进一步提高算法的效率。

图1 点扩散示意Fig.1 The schematic of point spreading

图2 约束窗口Fig.2 Constraint window

图3 各组数据的匹配结果Fig.3 Matching results of each experimental data set
[1] YU L,ZHANG D,HOLDEN E J.A Fast and Fully Automatic Registration Approach Based on Point Features for Multi Source Remote Sensing Images[J].Computers& Geosciences,2008,34(7):838-848.
[2] WONG A,CLAUSI D A.ARRSI:Automatic Registration of Remote Sensing Images[J].IEEE Transactions on Geoscience and Remote Sensing,2007,45(5):1483-1493.
[3] LOWE D G.Distinctive Image Features from Scale-invariant Keypoints[J].International Journal of Computer Vision, 2004,60(2):91-110.
[4] LI Xiaoming,ZHENG Lian,HU Zhanyi.SIFT Based Automatic Registration of Remotely Sensed Imagery[J].Journal of Remote Sensing,2006,10(6):885-892.(李晓明,郑链,胡占义.基于SIFT特征的遥感影像自动配准[J].遥感学报,2006,10(6):885-892.)
[5] YUAN Xiuxiao,LI Ran.A SIFT Image Match Method with Match-support Measure for Multi-source Remotely Sensed Images[J].Geomatics and Information Science of Wuhan University,2012,37(12):1438-1442.(袁修孝,李然.带匹配支持度的多源遥感影像SIFT匹配方法[J].武汉大学学报:信息科学版,2012,37(12):1438-1442.)
[6] DAI Jiguang,SONG Weidong,JIA Yonghong,et al.A New Automatically Matching Algorithm for Multi-source High Resolution Optical Satellite Images[J].Acta Geodaetica et Cartographica Sinica,2013,42(1):80-86.(戴激光,宋伟东,贾永红,等.一种新的异源高分辨率光学卫星遥感影像自动匹配算法[J].测绘学报,2013,42(1):80-86.)
[7] LÜJinjian,WEN Gongjian,LI Deren,et al.A New Method Based on Spatial Relations for Feature Matching[J].Acta Geodaetica et Cartographica Sinica,2008,37(3):367-373.(吕金建,文贡坚,李德仁,等.一种新的基于空间关系的特征匹配方法[J].测绘学报,2008,37(3):367-373.)
[8] YUE Chunyu,JIANG Wanshou.An Automatic Registration Algorithm for SAR and Optical Images Based on Geometry Constraint and Improved SIFT[J].Acta Geodaetica et Cartographica Sinica,2012,41(4):570-576.(岳春宇,江万寿.几何约束和改进SIFT的SAR影像和光学影像自动配准方法[J].测绘学报,2012,41(4):570-576.)
[9] LI Q L,WANG G Y,LIU J G.Robust Scale-invariant Feature Matching for Remote Sensing Image Registration [J].IEEE Geoscience and Remote Sensing Letters,2009, 6(2):287-291.
[10] ZHANG Qian,JIA Yonghong,HU Zhongwen.An Improved SIFT Algorithm for Mutli-source Remote Sensing Image Registration[J].Geometrics and Information Science of Wuhan University,2013,38(4):455-459.(张谦,贾永红,胡忠文.多源遥感影像配准中的SIFT特征匹配改进[J].武汉大学学报:信息科学版,2013,38(4):455-459.)
[11] JIANG S H,WANG C,XU X J,et al.Fast Algorithm for Multi-Source Image Registration Based on Geometric Feature of Corners[C]∥Proceedings of the 6th International Conference on Intelligent Computing.Changsha:Springer, 2010:438-446.
[12] ZHU Qing,WU Bo,ZHAO Jie.A Reliable Image Matching Method Based on Self-adaptive Triangle Constraint[J].Chinese Journal of Computers,2005,28(10):1734-1739.(朱庆,吴波,赵杰.基于自适应三角网约束的可靠影像匹配方法[J].计算机学报,2005,28(10):1734-1739.)
[13] WU B,ZHANG Y,ZHU Q.A Triangulation-based Hierarchical Image Matching Method for Wide-Baseline Images [J].Photogrammetric Engineering&Remote Sensing, 2011,77(7):695-708.
[14] YANG Huachao,ZHANG Shubi,ZHANG Qiuzhao.Least Squares Matching Methods for Wide Base-line Stereo Images Based on SIFT Features[J].Acta Geodaetica et Cartographica Sinica,2010,39(2):187-194.(杨化超,张书毕,张秋昭.基于SIFT的宽基线立体影像最小二乘匹配方法[J].测绘学报,2010,39(2):187-194.)
[15] YANG Huachao,YAO Guobiao,WANG Yongbo.Dense Matching for Wide Base-line Stereo Images Based on SIFT [J].Acta Geodaetica et Cartographica Sinica,2011,40(5): 537-543.(杨化超,姚国标,王永波.基于SIFT的宽基线立体影像密集匹配[J].测绘学报,2011,40(5):537-543.)
[16] YANG Huachao,ZHANG Lei,YAO Guobiao,et al.An Automated Image Registration Method with High Accuracy Based on Local Homography Constraint[J].Acta Geodaetica et Cartographica Sinica,2012,41(3):401-408.(杨化超,张磊,姚国标,等.局部单应约束的高精度图像自动配准方法[J].测绘学报,2012,41(3):401-408.)
[17] LI Fangfang,JIA Yonghong.Improved SIFT Algorithm and Its Application in Automatic Registration of Remotelysensed Imagery[J].Geomatics and Information Science of Wuhan University,2009,34(10):1245-1249.(李芳芳,贾永红.SIFT算法优化及其用于遥感影像自动配准[J].武汉大学学报:信息科学版,2009,34(10):1245-1249.)
[18] POLLARD S,PORRILL J,MAYHEW J,et al.Disparity Gradient,Lipschitz Continuity Binocular Correspondence [C]∥Proceedings of Robotics Research:The Third International Symposium.Gouvieux:MIT Press,1986:189-210.
[19] WU B,ZHANG Y,ZHU Q.Integrated Point and Edge Matching on Poor Textural Images Constrained by Selfadaptive Triangulations[J].Journal of Photogrammetry and Remote Sensing,2012(68):40-55.
[20] CHUM O.Two-view Geometry Estimation by Random Sample and Consensus[D].Prague:Czech Technical University,2005.
[21] ZHANG Dengrong,CAI Zhigang,YU Le.Study on Image Automatism Registration Methods Based on Matching[J].Journal of Zhejiang University:Engineering Science, 2007,41(3):402-406.(张登荣,蔡志刚,俞乐.基于匹配的遥感影像自动纠正方法研究[J].浙江大学学报:工学版, 2007,41(3):402-406.)
(责任编辑:陈品馨)
Progressive SIFT Matching Algorithm for Multi-source Optical Satellite Images
DAI Jiguang,SONG Weidong,LI Yu
School of Geomatics,Liaoning Technical University,Fuxin 123000,China
Considering the low matching rate of SIFT for multi-source optical satellite images,based on SIFT matching method,initial controlling points constrained by the relative scale and main orientation of SIFT features are extracted in this paper.Then,Delaunay triangulation is built by initial matching points.Local geometrical constraint model is built through point spreading.Finally,on the basis of the main orientation of features,minimum Euclidean distance criterion and local RANSAC algorithm,the matching of multi-source optical satellite images is progressively achieved with high accuracy.Compared with other matching algorithms,in the case of large scale and rotate images,the proposed algorithm has significant advantages in terms of matching amount and precision.
progressive;multi-source;SIFT;matching;point spreading
DAI Jiguang(1978—),male,PhD,lecturer, majors in remote sensing image processing and application.
P237
A
1001-1595(2014)07-0746-07
2013-07-01
戴激光(1978—),男,博士,讲师,研究方向为遥感图像处理与应用。
E-mail:daijg03@163.com
DAI Jiguang,SONG Weidong,LI Yu.Progressive SIFT Matching Algorithm for Multi-source Optical Satellite Images[J].Acta Geodaetica et Cartographica Sinica,2014,43(7):746-752.(戴激光,宋伟东,李玉.渐进式异源光学卫星影像SIFT匹配方法[J].测绘学报,2014,43(7):746-752.)
10.13485/j.cnki.11-2089.2014.00
国家自然基金(41271374;41101452);辽宁工程技术大学校基金(SCDY2013016)
修回日期:2014-05-25

