基于阿尔法形态的三维色域体积快速算法
孙 婧,徐 岩,李桂苓
(天津大学 电子信息工程学院,天津 300072)
基于阿尔法形态的三维色域体积快速算法
孙 婧,徐 岩,李桂苓
(天津大学 电子信息工程学院,天津 300072)
随着各种宽色域显示设备的出现,越来越需要高效准确的色域比较评价方法。三维色域由于包含了亮度信息,与二维色域相比,能够更全面地展示、比较色域差异。但由于其形状不规则,三维色域的计算较困难,高计算复杂度限制了三维色域评价在实时性要求较高的工程领域的应用。实现了基于阿尔法形态的三维色域体积计算方法。实验结果表明,通过仔细选择半径参数,能够以较低计算复杂度准确计算不规则三维色域体积。与基于准蒙特卡洛的体积计算方法相比,基于阿尔法形态的方法更适合实时应用。
三维色域;体积计算;阿尔法形态
目前通常用二维空间色域表示显示器能够重显的色彩范围,而色彩实际上是一个三维的量,各种可用来表示颜色的色空间(如XYZ,RGB,Luv,Lab)都是三维色空间。在二维空间计算色域及色域覆盖率忽略了亮度级别对色域范围的影响,所得结果不能充分反映色彩重显特性。因此,需要在包含亮度信息的三维空间中计算色域及色域覆盖率。目前已有一些计算三维色域体积的算法被提出。Bangyong Sun等[1]提出了CIE LAB色空间的液晶显示器色域描述算法。该算法在CIE LAB色空间利用Delaunay(德洛涅)三角剖分技术将色域边界面分割成小三角形。取中心点并将其与表面划分的三角形相连形成四面体,求所有四面体之和得到三维色域体积。Andreas Willert等[2]分别在CMY及CMYK色空间按亮度将色域体积均分成一系列薄片,在每个薄片上划分网格计算其色域大小。况盛坤等[3]采用基于空间区域分割的四面体网格剖分算法实现数字输出设备色域的三维立体再现和色域体积的求取。该算法将色度坐标数据转化为球面坐标,分别将色相角和仰角均分成N份,从而将整个颜色空间分成N×N个子区域进行计算。李超等[4]根据Delaunay理论在三维空间的扩展,将不规则的颜色空间立体分解为多个四面体网格进行色域体积的计算。该算法将分解得到的所有四面体体积相加,并没有考虑到色域立体表面的凹凸程度可能与分割成的四面体网格表面不一致。现有这些求三维体积快速算法多针对凸包,将色域表面作为光滑的凸面进行处理。实际上,从实测数据重构出的显示器三维色域立体可以看出,在设备无关色空间,显示器三维色域是凸包与凹坑相混合的不规则立体,用已有算法进行计算多会产生误差,结果并不准确。
本文致力于开发一种高效的色域体积计算方法。
1 阿尔法形态(Alpha Shapes)算法
对于一组给定的无序样点,阿尔法形态算法能够高效地提取离散点的轮廓并重构其几何形状。设二维空间中的有限点集合S,阿尔法形态算法的基本思想是将一个半径为α的圆围绕给定的离散点集S滚动,如图1所示[5]。
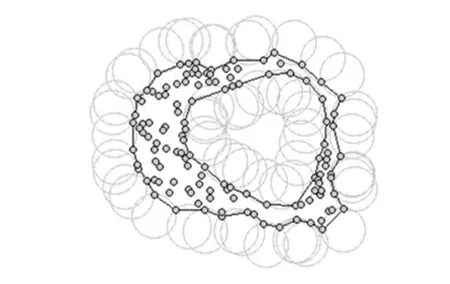
图1 阿尔法形态算法原理示意图
S的轮廓是一个多边形,由S和半径参数α决定。α控制多边形轮廓的精细程度。当α取值适当,这个圆就不会滚到S的内部,与圆相交的点就是S的边缘轮廓点,其滚动的痕迹就是S的边界线[5]。当α足够大时,所得多边形将为S的凸包。当α接近0时,S的边界线会通过S中的每一点。α取值对所得轮廓的影响如图2所示。

图2 半径参数对轮廓的影响示意图
设S中有n个点,可连接成n(n-1)/2条线,需要在其中找到位于边界的线。Edelsbruuner等[6]于1983年给出了阿尔法形态模型判断准则,根据这一准则可以确定边界线。判断条件如下:在点集S内任取两个点 p1和 p2,过这两点绘制半径为α的圆,若圆内没有其他点,则可认为 p1p2是边界线。Edelsbruuner等[7]于1994年从几何学的角度给出了三维阿尔法形态的原理,为其在工程领域的应用奠定了基础。Tomasz J.Cholewo等[8]于1999年提出一种基于阿尔法形态算法的面向彩色打印设备和彩色图像的色域边界提取算法。
2 三维色域体积计算
根据对多种不同宽色域显示设备的三维色域的观察,其形状均为不规则的凸包和凹坑的组合。其中一种在Luv空间的三维色域如图3所示(大部分色域是凸包,而在紫、红、黄、白区域为凹坑)。
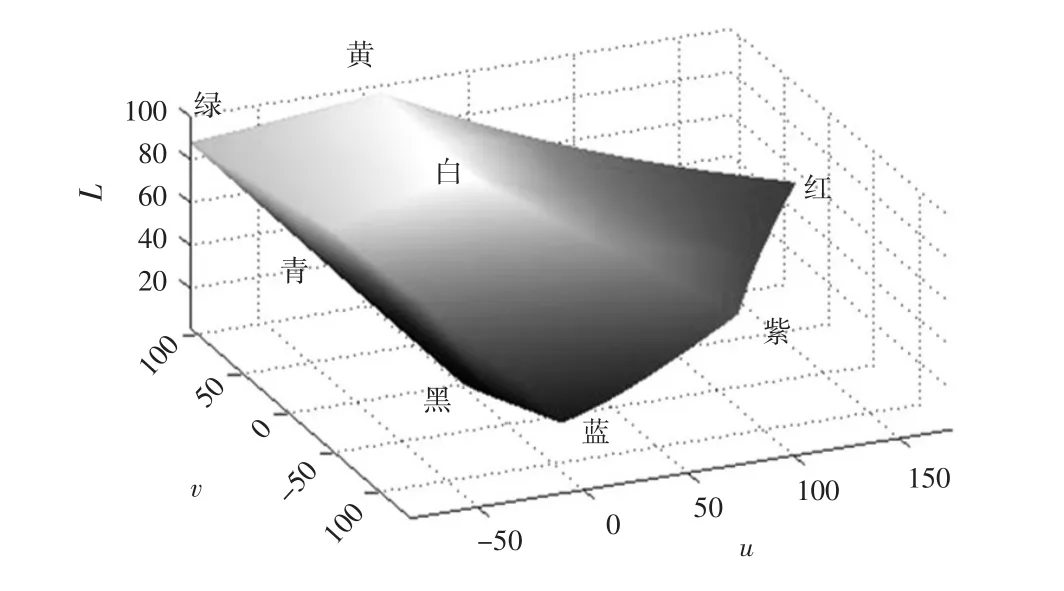
图3 Luv空间显示器色域
已知三维色域同时具有凸包和凹坑的特征,需要使用能同时适应两种情况的算法来计算其体积。如第1节所述,阿尔法形态法从原理上适用于凹坑和凸包两种情况。将阿尔法形态法扩展至三维[7-8],即可用来计算三维色域体积。
1)使用规范色域测试样本测试得到待测显示器的色域表面散点数据集S,S中的散点均为分布在三维色域表面上的点,集合S确定了该显示器的三维色域边界。
2)对点集S进行三角剖分,建立三维Delaunay三角网,得到N行4列的矩阵,N为分割的四面体的个数,矩阵的每行为分割成的四面体顶点的索引值。
3)利用Alpha Shapes算法原理对四面体进行筛除。对每一个单纯形四面体计算其外接圆半径R;对于给定的Alpha Shapes半径参数α,仅保留R<α的四面体;经过筛除之后,所剩小四面体的外边界面即为三维色域体积的边界面。
4)可视化步骤3)所得三维色域的边界面,即可视化筛除后所剩小四面体的外界面,通过改变α的大小,控制得到的边界面的精细程度。若边界面有空洞不连续,表示当前α值过小,增大α值,重复步骤3);若边界面连续但空间位置位于S中散点之下,表示当前α值仍然过小,增大α值,重复步骤3);若边界面连续但空间位置位于S中散点之上,表示当前α值过大,减小α值,重复步骤3);调整α值直至边界面连续且与S中散点重合,表明此时所取α值大小正好,其重构的边界面的凹凸程度与实际色域表面的凹凸程度一致。
5)对符合条件的四面体分别计算其体积,再将所有的体积相加即得到三维色域的体积。
3 实验结果
根据课题组对大量显示设备的色度测试和三维色域可视化实验,设备无关色空间如Luv中的三维色域边界面对应于RGB色立体的6个面,相邻面的交线对应于RGB色立体的12条边以及RGB色立体表面上连接白-红、白-绿、白-蓝、黑-黄、黑-青、黑-紫的6条线,共18条线。在实际应用中,为减少色度测试样点,每条边上取10个测试样点,形成如图3所示的三维色域。
应用第2节所述的扩展的阿尔法形态算法计算Luv空间中三维色域的体积。算法运行于HP 400-021cx台式电脑(2.9 GHz CPU,4 Gbyte ROM),运行环境为Win⁃dows7,MATLAB 2012a。表1给出当α取不同值时计算体积值与所用时间。

表1 α取不同值时计算体积值与所用时间
半径参数α取不同值时的实验结果如图4所示,可以看出α值越大,所形成的边界就越凸。经实验测试,当α<45时,算法无法重构色域表面(出现空洞);当45<α<50,重构表面略低于测试样点;当50<α<200,重构轮廓与测试样点一致。
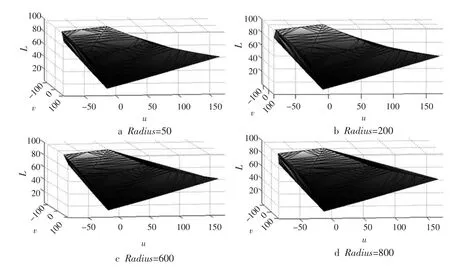
图4 α取不同值时计算色域体积
由实验结果可以看出,通过仔细选取半径参数,阿尔法形态法能够在较短时间内计算出色域体积。
准蒙特卡洛方法是应用于多重积分、面积和体积计算的统计方法[9]。为比较基于阿尔法形态的算法和基于准蒙特卡洛积分的方法,在同一实验平台上实现了准蒙特卡洛体积计算算法。准蒙特卡洛算法原理是随机取采样点,根据落在色域内的点的比例计算色域体积。本文实验选取了多个不同随机采样点数N,N服从均匀分布,分别运行10次,取均值作为结果。实验结果如表2所示。实验中N的最大值为6.7×106,因为更大的N值会导致系统内存溢出。
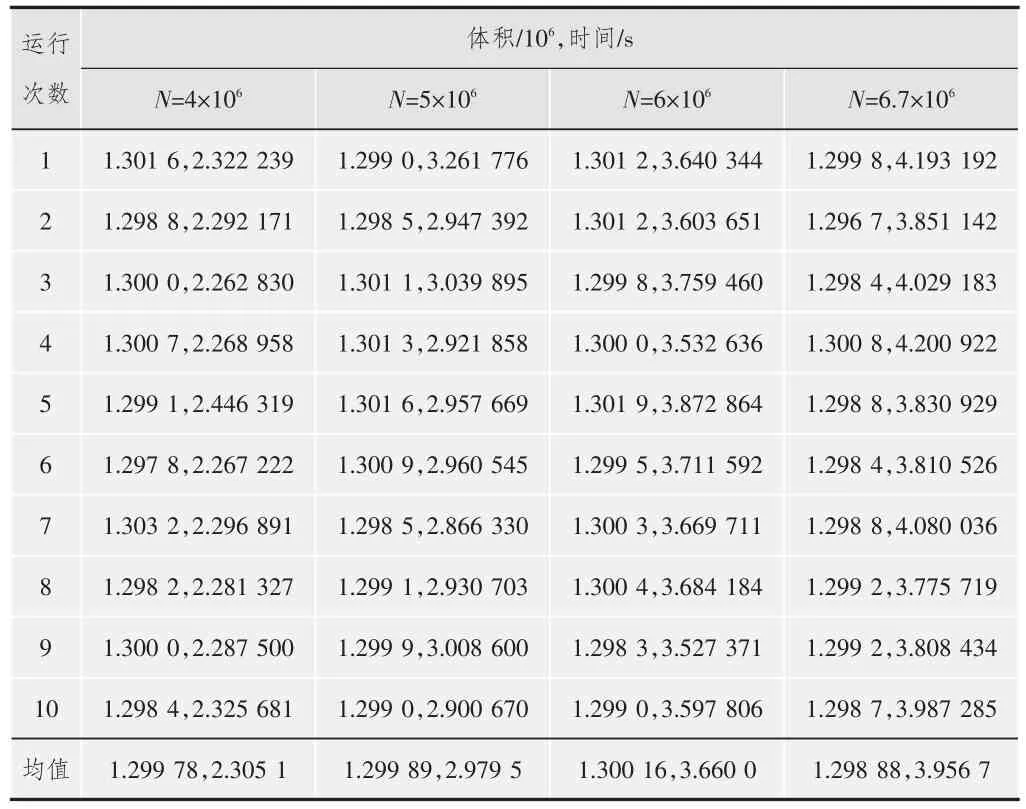
表2 准蒙特卡洛积分计算色域体积
需要指出的是,表2中所列时间不包括将测试数据分成12个面、分别对12个面进行曲面拟合,以及找到准蒙特卡洛边界条件的时间。考虑到这一点,可以看出基于阿尔法模型的体积计算方法比基于准蒙特卡洛算法的体积计算方法效率高,更适合实时应用。而且,准蒙特卡洛算法的精确度与N的平方根成正比、算法复杂度与N成正比,对硬件要求较高,限制了其在普通配置测试平台上的应用。
4 结论
在三维空间比较色域能比二维色度图提供更多信息。然而由于在设备无关色空间中色域是凸包和凹坑的不规则组合,高计算复杂度限制了其在实时应用领域中的应用。本文使用扩展的阿尔法形态算法计算三维色域体积。实验结果表明该方法能高效重构边界轮廓、计算色域体积。集成该方法的三维色域处理平台可为显示器生产商和测试机构提供高效的三维色域比较、评价手段。
目前,实验中半径参数α的选取仍需人工决定。接下来的工作中将进一步研究能自适应选取最佳α值的方案。
[1] SUN B,LIU H,LIW,et al.A color gamut description algorithm for liquid crystal displays in CIELAB space[J].The Scientific World Journal,2014(2014):1-9.
[2]WILLERT A,FLASPOHLER M,HUBLER A C.Calculating a col⁃or gamut border using a grid approach[C]//Proc.Conference on Co⁃lour in Graphics,Imaging,and Vision.[S.l.]:Society for Imaging Science and Technology,2004:156-160.
[3] 况盛坤,王晓红,吕兆锋.基于空间区域分割的四面体网格剖分色域描述算法[J].包装工程工程版,2014,35(5):126-130.
[4] 李超,王彩印.基于空间四面体网格的色域计算与比较研究[J].中国印刷与包装研究,2010(S1):102-106.
[5] WU Z,QIL,LUO P,et al.Edge-preservingmulti-scale image de⁃composition based on alpha-shape[C]//Proc.Conference Anthology,IEEE.Beijing:IEEE Press,2013:1-5.
[6] EDELSBRUNNER H,KIRKPATRICK D,SEIDEL R.On the shape of a set of points in the plane[J].IEEE Trans.Information Theory,1983,29(4):551-559.
[7] EDELSBRUNNER H,MUCKE E P.Three-dimensional alpha shapes[J].ACM Trans.Graphics,1994(13):43-72.
[8]CHOLEWO T J,LOVE S.Gamut boundary determination using al⁃pha-shapes[C]//Proc.the 7th Color Imaging Conference.Scottsdale: [s.n.],1999:200-204.
[9] NIEDERREITER H.Random number generation and quasi monte Carlomethods[M].Philadelphia:SIAM,1992.
3D Color Gamut Volume Calculation A lgorithm Based on Alpha Shapes
SUN Jing,XU Yan,LI Guiling
(School of Electronics Information Engineering,Tianjin University,Tianjin 300072,China)
With the emerging of different kinds of wide color gamut displays,evaluation and comparison of their color gamut are required more.3D color gamut is known as a better way to demonstrate gamut difference and provide more information than conventional 2D color gamut as it incorporates luminance information.Because of its irregular shape,the calculation of 3D color gamut is relatively difficult and complex.High computational complexity restricts its application in real time cases.In this paper,an Alpha shapes algorithm on PC for 3D color gamut volume calculation is implemented.Experiment results show that this method can accurately compute the volume of the irregular shaped gamut with relatively low computational complexity by carefully choosing the radius parameter.Compared with quasi-Monte-Carlo-based method,Alpha-shapes-based method is more suitable for real time cases.
3D color gamut;volume calculation;Alpha shapes
TN873
A
�� 薇
2014-08-11
【本文献信息】孙婧,徐岩,李桂苓.基于阿尔法形态的三维色域体积快速算法[J].电视技术,2014,38(21).
孙 婧,女,硕士生,主研信息号信息处理、数字视频与多媒体技术;
徐 岩,女,副教授,硕士生导师,主要从事信息号信息处理、数字视频与多媒体技术教学、科研工作;
李桂苓,教授,博士生导师,主要从事信息号信息处理、数字视频与多媒体技术教学、科研工作。

