常用稳健估计方法在坐标系统转换中的有效性比较

□董巧玲 王冠儒

（太原理工大学矿业工程学院测绘科学与技术系，山西太原030024）

常用稳健估计方法在坐标系统转换中的有效性比较

□董巧玲 王冠儒

（太原理工大学矿业工程学院测绘科学与技术系，山西太原030024）

在进行GNSS坐标系统之间相互转换的坐标拟合时，多采用基于最小二乘估计来研究不同的拟合方法，这就要求参与建模的观测数据不包含粗差，一旦将粗差引入模型，就会造成参数的最小二乘估计结果失真。而稳健估计方法能有效地消除或减弱粗差对参数估计的影响。本文探讨了基于四参数和七参数模型坐标系统转换中，当观测值中包含粗差时几种常用稳健估计方法（Huber法、Tukey法、Danish法、IGGIII方案）的相对有效性，对于稳健估计方法的选取具有一定的参考价值。

稳健估计；粗差；坐标转换

1.引言

自1953年G.E.P.BOX首先提出稳健性（Robustness）的概念，Tukey、Huber、Hampel、Rousseeuw等人对参数的稳健估计进行了卓有成效的研究[1]，1980年，丹麦的Krarup和Kubik等人将稳健估计理论引入了测量界，1989年，周江文研究员针对测量平差中不等权观测值普遍存在的情况下，提出了等价权原理，解决了不同精度独立观测的权函数的确定的问题。由于稳健估计能够比较好的处理测量原始数据含有粗差的问题，从此在测量界掀起了对稳健估计研究的热潮，这些研究扩充了稳健估计方法的成果，为进一步理论研究和在测绘中应用打下了基础。坐标系统之间的转换是应用GNSS定位技术不可避免的问题[2]。近代以来，随着3S等先进测量技术的发展以及测量数据采集的现代化和自动化，在某种意义上，粗差也不可避免地被包含在了平差模型之中[3]。由于最小二乘法对含有粗差的观测量相当敏感，个别粗差就会对参数的估值产生较大的影响[1]，此时，在测量数据服从正态分布情况下具有最优统计性质的经典最小二乘法就不能满足高精度测量的需要。针对最小二乘估计这一缺陷便提出了具有一定抵抗粗差能力的稳健估计方法。稳健估计（Robust Estimation）理论旨在构造某种估计方法，使其对于粗差具有较强的抵抗能力。它与经典的估计理论不同的是，稳健估计理论中讨论的最优是在抗差的前提下的最优[3]。坐标系统转换的实质是求解坐标系统转换参数[4]。在平面直角坐标转换中，较常用的是四参数的相似变换法，即2个平移参数、1个缩放参数和1个旋转参数。在三维直角坐标转换中，较常用的是较严密的七参数相似变换法，即3个平移参数，1个尺度比参数和3个旋转参数。本文以算例探讨了将粗差加入坐标观测值中，几种稳健估计方法之间以及与LS法对减弱或消除粗差的有效性比较，在观测值中存在粗差的情况下，为合适地选择参数估计方法提供了初步依据。

2.几种常用的稳健估计方法

（1）Huber法[5]：

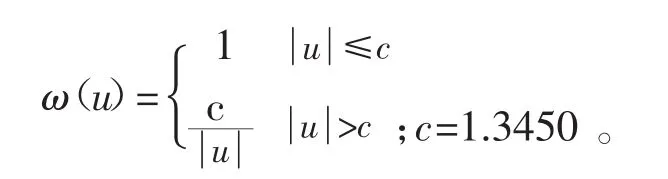
（2）Tukey法[6]：

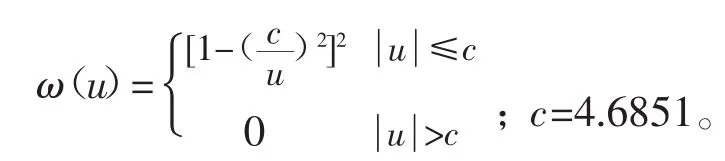
（3） Danish法[1]：

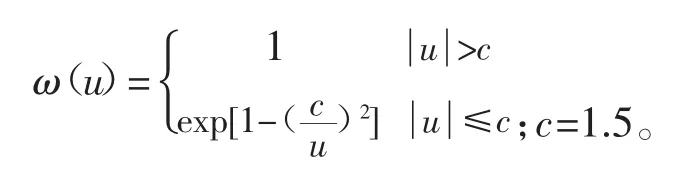
（4） IGGIII方案[7，8]：

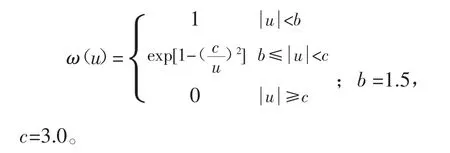
3.坐标系统转换模型

3.1四参数坐标系统转换模型

P坐标系统下坐标转换到Q坐标系统下坐标的四参数模型为[9]：

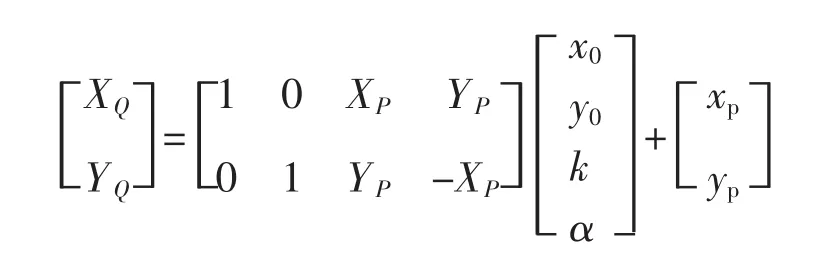
式中：XP和YP表示P坐标系统下的坐标；XQ和XQ表示Q坐标系统下的坐标；x0、y0、k和α是P坐标系统转换到Q坐标系统的坐标转换参数，它们分别表示两个平移参数、一个缩放参数和一个旋转参数。

四参数坐标系统转换算例如下：

本算例选取将一组北京54坐标转化为西安80下的坐标中的5个重合点，其观测数据见表1[10]。P、Q分别表示P、Q坐标系统下坐标的观测值。由LS法求得中误差约为± 0．3cm，i表示在第i个观测值加入6cm（约为20倍的单位权中误差由于算例中数据有限，加入10倍中误差作为粗差，各估计方法减弱或消除粗差的效果不明显，故选用20倍中误差作为粗差）的粗差，j表示第j个观测值加入6cm（同上）的粗差，g表示观测值中加入粗差的个数。观测值中加入粗差后改正数解算结果见表2、表3。

由于通常以三倍或两倍中误差作为偶然误差的极限值，本文中取三倍中误差作为偶然误差的极限值。本算例中若含有粗差的观测值的改正数大致落在v∈（5.1，6.9）cm范围内说明估计方法在一定程度上检测出了粗差，能有效减弱或消除粗差对平差结果的影响。

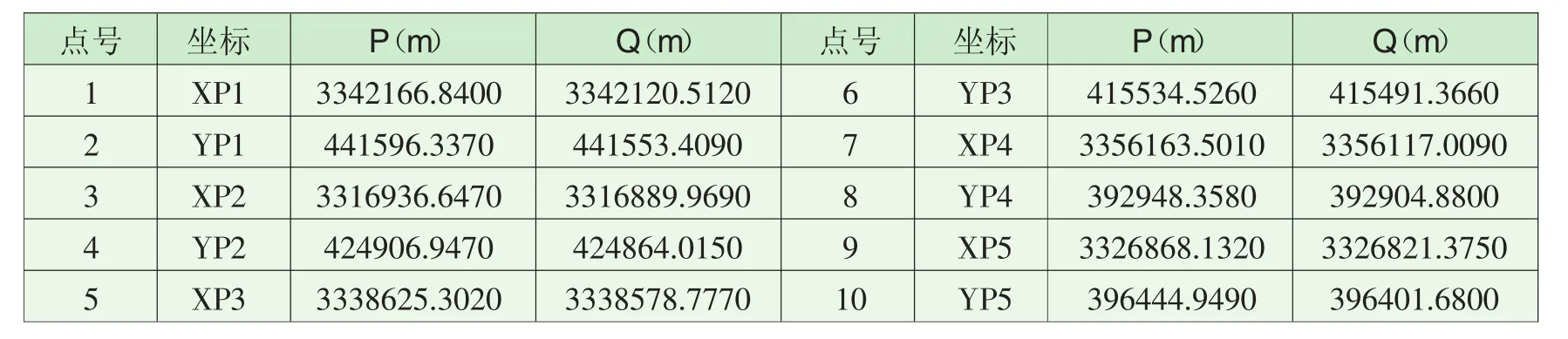
表1 五重合点四参数坐标系统转换的观测数据Tab.1 Observation data of four-parameter coordinate system transformation with five coincident points

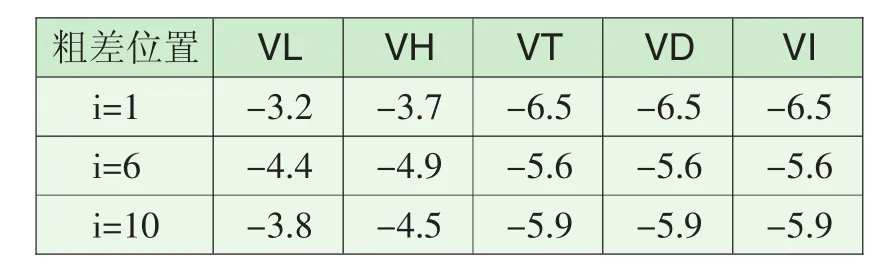
表2 LS和不同稳健估计方法的改正数（四参数，5重合点，g=1）Tab.2 Corrections of LS and different robust estimation methods（four-parameter，five coincident points，g=1）

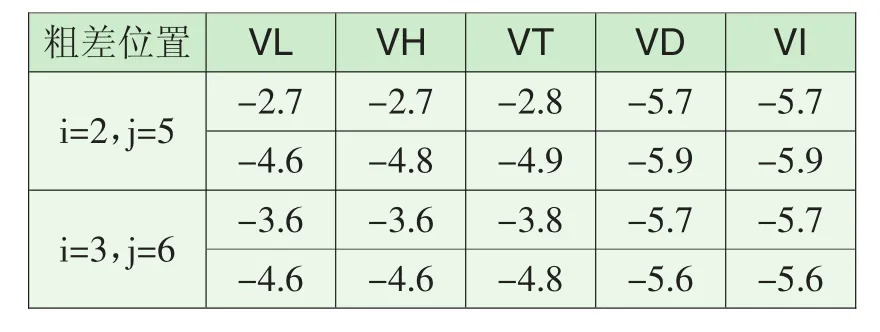
表3 LS和不同稳健估计方法的改正数（四参数，5重合点，g=2）Tab.3 Corrections of LS and different robust estimation methods（four-parameter，five coincident points，g=2）

将表2和表3中不同估计方法解算的改正数同值域v比较，可知在已知粗差大小和位置的情况下，当g=1时，Tukey法、Danish法、IGGIII方案比LS法、Huber法更能有效地消除和减弱粗差对平差结果的影响；当g=2时，Danish法、IGGIII方案比Huber法、Tukey法、LS法能同时更有效地减弱或消除不同位置上粗差对平差结果的影响。

3.2七参数坐标系统转换模型

P坐标系统下坐标转换到Q坐标系统下坐标的七参数模型（Bursa模型）是[3]：

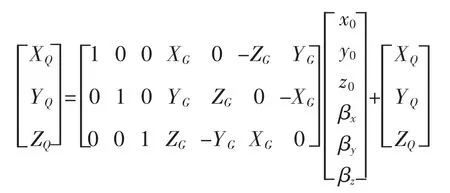
式中，XP、YP和ZP表示P坐标系统下的坐标；XQ、YQ和ZQ表示Q坐标系统下的坐标；x0、y0、z0、βx、βy和 βz分别是三个平移参数、一个缩放参数和三个旋转参数。

七参数坐标系统转换算例如下：

本算例选取三维小角度直角坐标转换中6个重合点，其观测数据见表4[11]。P、Q分别表示P、Q坐标系统下坐标的观测值。由LS法求得中误差约为±0.5cm，i表示在第i个观测值加入5cm（约为10倍的单位权中误差）的粗差，j表示第j个观测值加入5cm（同上）的粗差，g表示观测值中加入粗差的个数。观测值中加入粗差后改正数解算结果见表5、表6。

同上个算例相同，取三倍中误差作为偶然误差的极限值。本算例中若含有粗差的观测值的改正数大致落在v'∈（3.5，6.5）cm范围内说明估计方法在一定程度上检测出了粗差，能有效减弱或消除粗差对平差结果的影响。

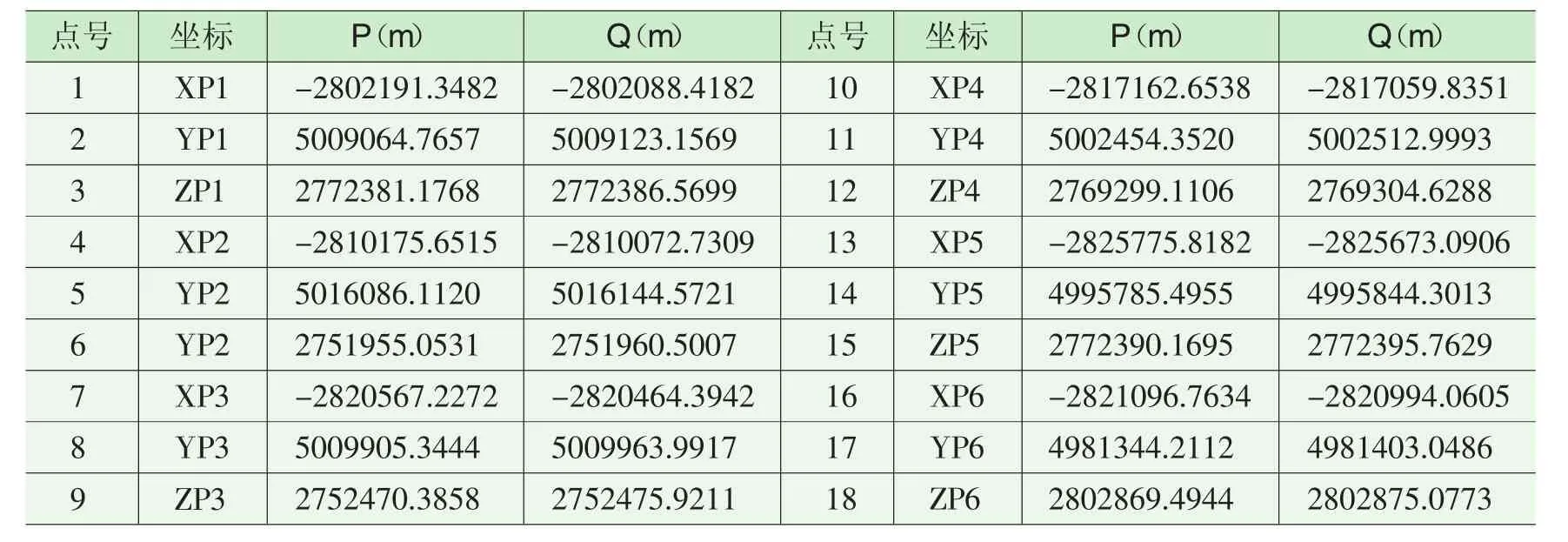
表4 六重合点七参数坐标系统转换的观测数据Tab.4 Observation data of seven-parameter coordinate system transformation with six coincident points

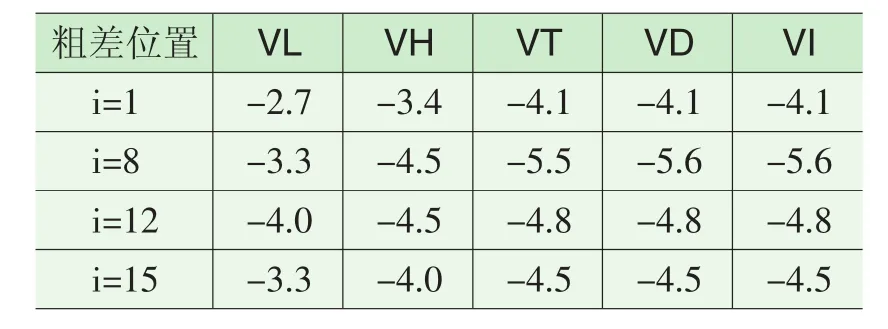
表5 LS和不同稳健估计方法的改正数（七参数，6重合点，g=1）Tab.5 Corrections of LS and different robust estimation methods（seven-parameter，six coincident points，g=1）

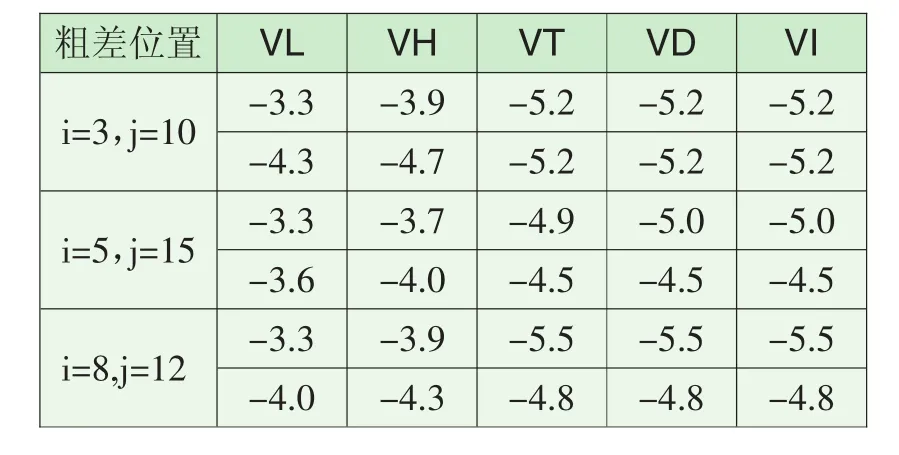
表6 LS和不同稳健估计方法的改正数（七参数，6重合点，g=2）Tab.6 Corrections of LS and different robust estimation methods（seven-parameter，six coincident points，g=2）

将表5和表6中不同估计方法解算的改正数同值域比较，可知在已知粗差大小和位置的情况下，当g=1时，Tukey法、Danish法、IGGIII方案比LS法、Huber法能更有效地消除或减弱粗差对平差结果的影响；当g= 2时，Tukey法、Danish法、IGGIII方案比Huber法、LS法能同时更有效地减弱或消除不同位置上粗差对平差结果的影响。

4.结语

本文通过算例研究了在四参数和七参数模型坐标系统转换的观测值包含粗差的情况下，通过分析比较稳健估计的Huber法、Tukey法、Danish法、IGGIII方案和LS法解算结果的改正数可知，在一定的条件下，Tukey法、Danish法、IGGIII方案比Huber法、LS法能更有效地消除或减弱粗差对参数估计结果的影响。当粗差个数或位置改变时，稳健估计各方法对于减弱或消除粗差的有效性会有一定的改变，一般情况下，Danish法、IGGIII方案具有相对较好的有效性。究其原因，观测数据的相关性、粗差存在位置、粗差个数、粗差的大小等可能是造成其有效性改变的影响因素。本文为坐标系统转换如何选择更恰当的估计方法提供了一定的依据。

【1】王新洲，陶本藻，邱卫宁等.高等测量平差[M].测绘出版社，2006：73-74.

【2】郭英起，唐彬，张秋江，等.基于空间直角坐标系的高精度坐标转换方法研究[J].大地测量与地球动力学，2012，32（3）：125-128.

【3】黄幼才等.数据探测与抗差估计[M].测绘出版社，1990：70-71.

【4】Li，H.F.Jiang，X.Q.and Li，Z.Robust estimation in Gaussian filtering for engineering surface characterization[J].Precision Engineering，2004，28（2）：186-193.

【5】Baselga，S.Globaloptimizationsolutionofrobustestimation[J].JournalofSurveyingEngineering，2007，133（3）：123-128.

【6】陆珏，陈义，郑波.总体最小二乘方法在三维坐标转换中的应用[J].大地测量与地球动力学，2008，28（5）：77-81.

【7】常志巧，郝金明，张成军等.GPS快速定位中病态问题的正则化抗差解法[J].大地测量与地球动力学，2008，28（3）：83-86.

【8】文援兰，杨元喜，王威.卫星精密轨道抗差估计的研究[J].空间科学学报，2001，21（4）：341-350.

【9】Ge，Y.H.Yuan，Y.and Jia，N.N.More efficient methods among commonly used robust estimation methods for GPS coordinate transformation[J].Survey Review，2012.

【10】王雪春.坐标转换的应用[EB/OL].http：//wenku.baidu.com/link?url=SAlS_FBcoY0HM－cP513fIHGCPEUpdbZs-OEvKpF9fTfr5HT3rAEiqCgW_w5GsdKPM76 iUbyKaX897L7xnJ5VyQ3v1 CdJrLGPTcWKREd-pMgG.

【11】杨仕平.整体最小二乘理论及其在变形监测中的应用研究[D].西南交通大学，2013：39-40.

王冠儒（1966年——），女，硕士，高工，毕业于太原理工大学，主要从事测量数据处理和实验室管理。

P207

A

2095-7319（2014）03-0057-05

董巧玲（1988年——），女，硕士，太原理工大学测绘科学与技术系，研究方向为空间数据采集方法和数据处理。