常用稳健估计方法在多元线性回归中的有效性比较

□刘君 余哲

（太原理工大学测绘科学与技术系，山西太原030024）

常用稳健估计方法在多元线性回归中的有效性比较

□刘君 余哲

（太原理工大学测绘科学与技术系，山西太原030024）

多元线性回归是一种在测量中应用广泛的参数估计方法，其回归参数通常基于LS法求得，但LS法不具备抵抗粗差的能力。在粗差不可避免的情况下，稳健估计能达到减弱粗差对参数估计的影响。本文就多元线性回归在测量中的应用进行研究，当观测值的不同位置含有不同数量的粗差时，探讨和比较常用稳健估计方法（Huber法、Tukey法、Danish法和IGGⅢ方案）在多元线性回归模型中的有效性，结果表明IGGⅢ方案比LS法和其他三种常用稳健估计方法更为有效。

多元线性回归；稳健估计；有效性比较

引言

多元线性回归是处理变量间相关关系的参数估计方法，在生产实践与科学实验中应用较为广泛，其回归参数通常基于最小二乘法（LS法）求得[1]。在数据采集时，观测值不可避免地会带有粗差。而LS法在计算过程中对每个观测值都赋予相同的权重，由此带来对粗差的处理不当，使回归系数估值产生较大偏差，从而影响了回归模型的有效性[2]。

为了消除或减弱粗差对参数估计的影响，1953年，G.E.P.BOX提出了稳健估计的概念。1964年，Huber发表的论文《定位参数的稳健估计》为稳健估计理论奠定了基础。1968年，Relles[3]提出了改进最小二乘稳健回归。1973年，Huber[4]提出把M-估计引入到回归分析中，并对最大似然估计回归的定义及其渐近性进行了理论与实证。1977年，Holland和Welsch[5]提出了选权迭代法。吴健平和张立[1]通过对LS法和稳健估计方法进行比较，指出稳健估计方法是LS法的改进，以地理数据中的一元线性回归为例，说明稳健估计能有效地减弱粗差对回归系数估值的影响，并且在回归过程中不用去判断哪些数据含有粗差。本文通过在算例中改变粗差的位置与数量来探讨和比较不同稳健估计方法在多元线性回归模型中的有效性。

1.多元线性回归模型

假设某一因变量受个自变量（x1，x2，…，xm）的影响，其 组观测值为yi，xi1，xi2，…，xim，（i=1，2，…，n）。则多元线性回归模型为：

yˆ=β0+β1xi1+β2xi2+…+βmxim+εi

式中：β0，β1，…，βm是未知参数，εi是随机误差，xi1，xi2，…，xim是m个可测量并可控制的非随机变量[6]。

2.常用的稳健估计方法

四种常见稳健估计方法的权函数如下。其中，u代表标准化的残差（ui=vi/σ），ω（u）表示权函数；a、b和c表示调和系数，均采用有关文献的推荐值。

（1）Huber法[7]：

（2）Tukey法[8]：

（3）Danish法[9]：

（4）IGGⅢ方案[10]：

3.算例

多元线性回归在测量中有着广泛的应用，如：利用LTS获得的点云数据采用切片分割法所得的株冠体积与冠高和冠高直径满足二元线性关系[11]；井下三角高程测量中钢尺丈量误差与高差、水平距和测站数满足三元线性关系[12]；福建半日潮区理论深度基准面值与分潮M2，S2，K1，O1四个主要分潮的平均振幅满足四元线性关系[13]等。本文主要以二元线性回归和四元线性回归为例，进行探讨和分析。

3.1二元线性回归的算例

用切片分割法所得的紫穗槐株冠体积y（dm3）与冠高x1（cm）、冠高直径x2（cm）满足二元线性关系。有15组观测数据如表1。

由LS法得观测值的单位权中误差为1.9，选择10倍左右的单位权中误差（+ 20dm3）作为粗差。下面设计了三种方案分别进行试验。其中，用n表示观测值的数量，g表示粗差的数量，i、j和k分别表示在第i个、第j个和第k个观测值中加入粗差（+ 20dm3）。

A1：在不同的位置加入一个粗差（n=15，g=1），结果见表2。

A2：在不同的位置加入两个粗差（n=15，g=2），结果见表3。

A3：加入三个粗差（n=15，g=3），结果见表4。

表1 二元线性回归算例的观测值Tab.1 The observations of binary linear regression

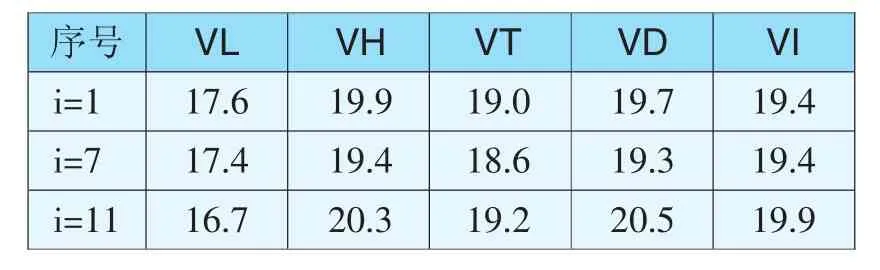
表2 二元线性回归LS法、Huber法、Tukey法、Danish法和IGGIII方案的残差（n=15，g=1）Tab.2 Residual of LS，Huber，Tukey，Danish and IGGIII robust estimation methods of binary linear regression（n=15，g=1）

表3 二元线性回归LS法、Huber法、Tukey法、Danish法和IGGIII方案的残差（n=15，g=2）Tab.3 Residual of LS，Huber，Tukey，Danish and IGGIII robust estimation methods of binary linear regression（n=15，g=2）

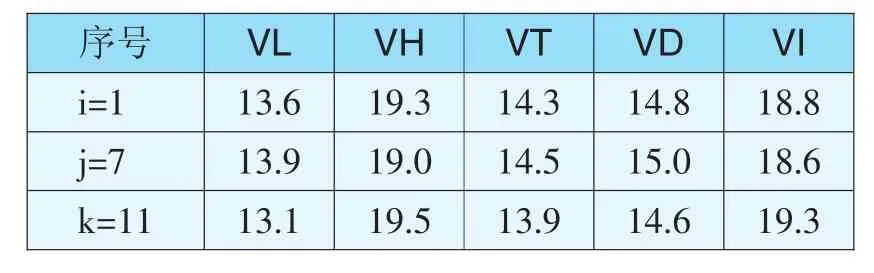
表4 二元线性回归LS法、Huber法、Tukey法、Danish法和IGGIII方案的残差（n=15，g=3）Tab.4 Residual of LS，Huber，Tukey，Danish and IGGIII robust estimation methods of binary linear regression（n=15，g=3）

将表2、表3和表4中各参数估计方法所得的残差与粗差相比较可知，在二元线性回归模型中，当g=1时，稳健估计方法（Huber法、Danish法、Tukey法和IGGIII方案）比LS法都能更有效地消除或减弱粗差对参数估计的影响，且四者有效性相差不大。当g=2时，稳健估计方法依然优于LS法，而且Huber法、Danish法和IGGIII方案比Tukey法更为有效。当g=3时，Huber法和IGGIII方案比LS法、Tukey法和Danish法能够更有效地消除或减弱粗差对参数估计的影响。

3.2四元线性回归的算例

福建半日潮区理论深度基准面值y与分潮M2，S2，K1，O1四个主要分潮的平均振幅x1，x2，x3，x4满足四元线性关系。有15组观测数据如表5。

由LS法得观测值的单位权中误差为3.2，选择10倍左右的单位权中误差（-30cm）作为粗差。下面设计三种方案分别进行试验。其中，用n表示观测值的数量，g表示粗差的数量，i、j和k分别表示在第i个、第j个和第k个观测值中加入粗差（-30cm）。

B1：在不同的位置加入一个粗差（n=15，g=1），结果见表6。

B2：在不同的位置加入两个粗差（n=15，g=2），结果见表7。

B3：加入三个粗差（n=15，g=3），结果见表8。

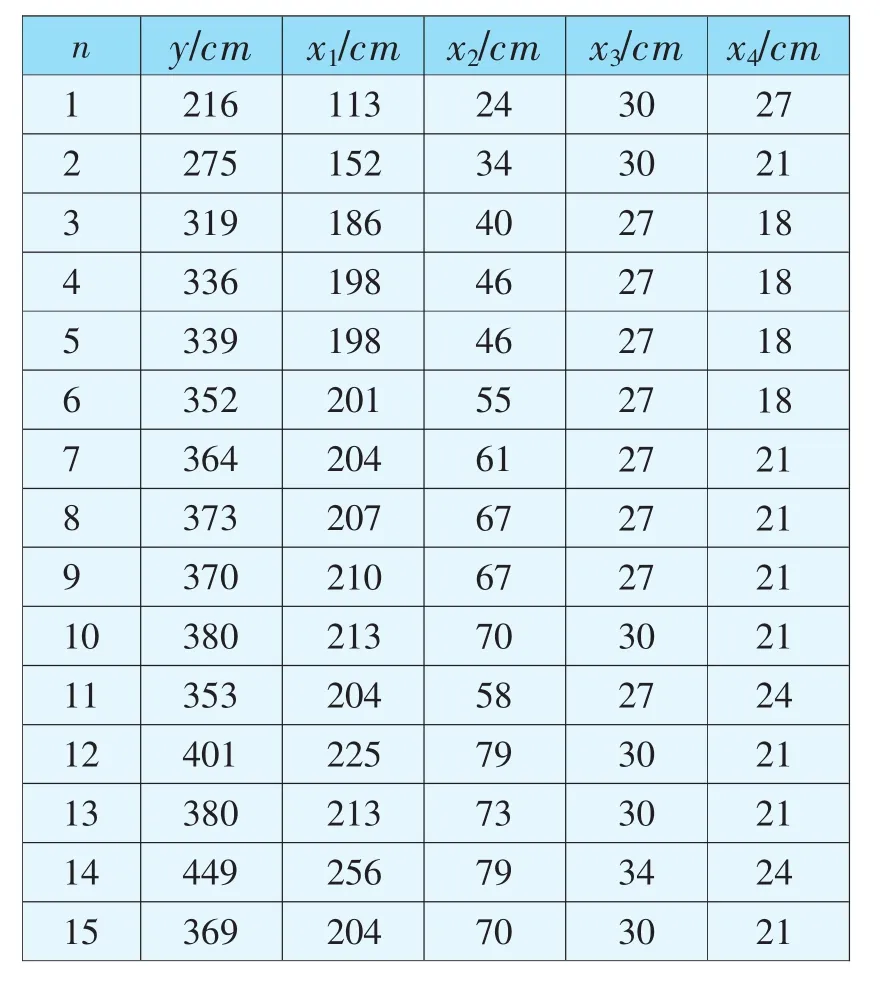
表5 四元线性回归算例的观测值Tab.5 The observations of quadruple linear regression

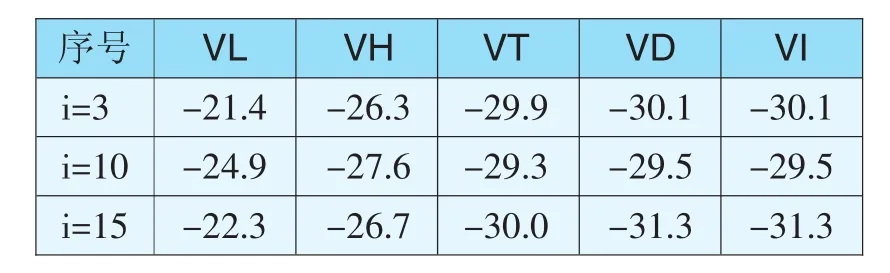
表6 四元线性回归LS法、Huber法、Tukey法、Danish法和IGGIII方案的残差（n=15，g=1）Tab.6 Residual of LS，Huber，Tukey，Danish and IGGIII robust estimation methods of quadruple linear regression（n=15，g=1）

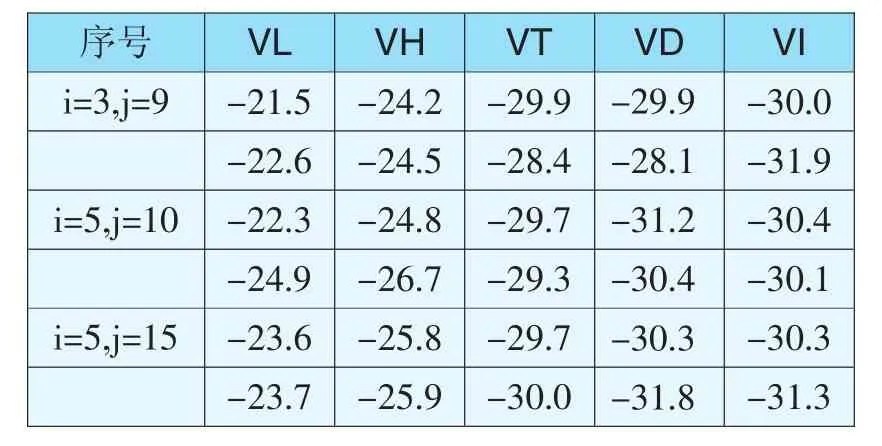
表7 四元线性回归LS法、Huber法、Tukey法、Danish法和IGGIII方案的残差（n=15，g=2）Tab.7 Residual of LS，Huber，Tukey，Danish and IGGIII robust estimation methods of quadruple linear regression（n=15，g=2）

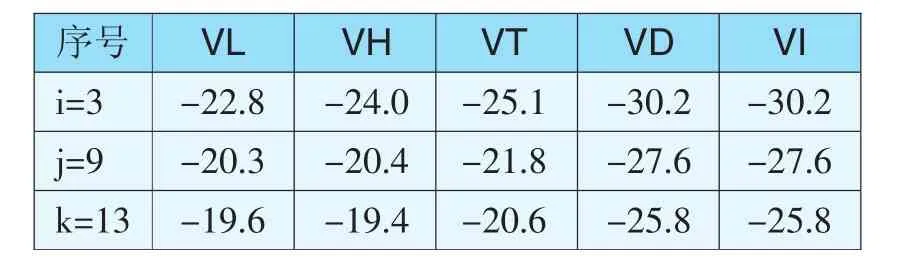
表8 四元线性回归LS法、Huber法、Tukey法、Danish法和IGGIII方案的残差（n=15，g=3）Tab.8 Residual of LS，Huber，Tukey，Danish and IGGIII robust estimation methods of quadruple linear regression（n=15，g=3）

将表6、表7和表8中各参数估计方法所得的残差与粗差相比较可知，在四元线性回归中，当g=1和g=2时，稳健估计方法（Huber法、Tukey法、Danish法和IGGIII方案）比LS法能够更有效地消除或减弱粗差对参数估计的影响，且Danish法、Tukey法和IGGIII方案相对Huber法更为有效。当g=3时，Danish法和IGGIII方案比LS法、Huber法和Tukey法能够更为有效地消除或减弱粗差对参数估计的影响。

4.结论

本文以二元和四元线性回归在测量中的应用为例，当观测值的不同位置有不同数量的粗差时，分析稳健估计方法（Huber法、Tukey法、Danish法和IGGIII方案）所得观测值的残差，结果表明四种常用稳健估计方法比LS法能更有效地在多元线性回归中消除或减弱粗差对参数估计的影响，其中，IGGIII方案比Huber法、Tukey法和Danish法在多元线性回归中消除或减弱粗差对参数估计的影响更为有效。

【1】吴健平，张立.地理数据线性回归中的稳健估计方法[J]．干旱区地理，1994，3（1）：83-88.

【2】陈艳国.回归预测模型的稳健性分析[J].工程地质计算机应用，2005，3（39）：22-25.

【3】Relies，D.A.Robust Regression by Modified Least[M].Ph.D.thesis，Yale Univ.1968.

【4】Peter J.Huber.Robust Regression：Asymptotics Conjectures and Monte Carlo[J].The Annals of Statistics，1973，（5）：799-821.

【5】P.W.Holland AND R.E.Welsch，Robust Regression Using Iteratively Reweighted Leastsquares[J].Commun Statist-Theor.Meth，A6（1977），pp.813-827.

【6】王新洲，陶本藻，邱卫宁等，高等测量平差[M]．测绘出版社，2006，4.

【7】Baselga，S.Global optimization solution of robust estimation[J].Journal of Surveying Engineering，2007，133（3）：123-128.

【8】Pennacchi，P.Robust estimate of excitations in mechanical systems using M-estimators-Theoretical background and numerical applications[J].Journal of Sound and Vibration，2008，310：923-946.

【9】Nathan L.Knight and Jinling Wang.A Comparison of Outlier Detection Procedures and Robust Estimation Methods in GPS Positioning[J].Journal of Navigation，2009，62：699-709.

【10】Chang，Z.Q.，Hao，J.M.，Zhang，C.J.，and Cui，J.Y.（2008）.'Regularization combined with robust estimation and its application for GPS rapid positioning.'J.G.G.，28（3），83-86.

【11】毕银丽，齐礼帅，陈书琳等，基于点云数据的株冠体积测量方法[J].科学报，2013，1（27）：31-36.

【12】王帅，高井祥，胡洪等，多元线性回归算法在井下三角高程测量中的应用研究[J].测绘与空间地理信息，2011.2：63-66.

【13】陈楠，福建半日潮去理论深度基准面值回归方程的建立[J].测绘通报，1999，9：28-29.

余哲(1963年——)，男，高工，硕士，毕业于太原理工大学，主要从事测量数据处理和开采沉陷。

P207

A

2095-7319（2014）03-0044-05

刘君（1990年——），女，毕业于太原理工大学测绘科学与技术系，硕士研究生，研究方向为空间数据采集方法和数据处理。