一种无直线逼近的高速高精度圆弧插补算法*

李伟光，曾顺星，叶国强，余 漳

(华南理工大学 机械与汽车工程学院，广州 510640)

0 引言

在数控系统中，为了提高插补运算的效率，由软件实现粗插补、硬件实现精插补的两级插补得到广泛应用。这种方式充分利用了软件的柔性和硬件的快速性、可靠性。为实现曲线轨迹的运动定位，在传统的两级插补中，粗插补通常采用直线逼近曲线，然后对直线进行精插补。然而直线逼近带来了决定插补轨迹轮廓精度的误差，需要引入复杂的误差控制机制;带来了速度与精度的矛盾;带来了大量离散化的微小直线段，造成数据存储和通信的负担及速度的波动，速度波动进一步导致无法实现高速进给。在曲线曲率变化大的情况下，这种现象尤为突出。

1 无直线逼近的圆弧插补算法原理

传统的两级插补算法由直线段组成的粗插补和微小直线段组成的精插补构成。两级插补的原理框图如图1 所示:

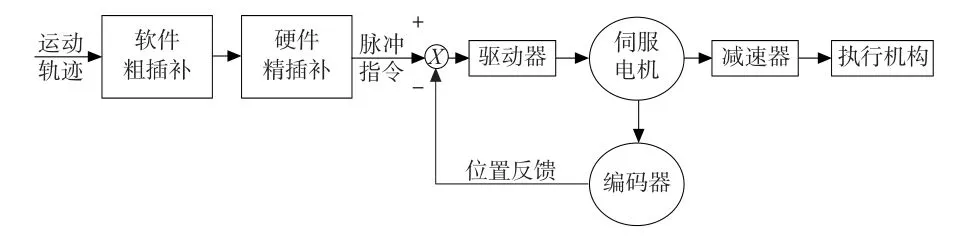
图1 两级插补原理框图

第一级插补预先执行，生成允许的最大进给步长。第二级插补调整进给步长来减小运动波动［1-2］。例如:圆弧插补中，粗插补以较大的弦线、切线或割线逼近圆弧，然后用微小线段进行直线精插补。

无直线逼近的高速高精度圆弧插补算法，粗插补不再以直线逼近曲线，直接以弧长为进给量计算出下一插补点，然后进行圆弧精插补，以避免直线逼近带来的逼近误差、精度与速度的矛盾和速度波动的问题。

下面以平面圆弧插补为例详述无直线逼近的圆弧插补算法的原理。

1.1 圆弧粗插补

圆弧粗插补基于时间分割法，采用极坐标系描述目标曲线。以弧长为进给量，以含方向的圆心角为增量，以其正负判断进给方向，计算出下一插补点的坐标［3］。不失一般性，在X-Y平面上，目标曲线圆弧方程为

目标曲线始于点S(Xs，Ys)，终止于点E(Xe，Ye)，当前点是Pi(Xi，Yi)，下一插补点是Pi+1(Xi+1，Yi+1)。如图2 所示:

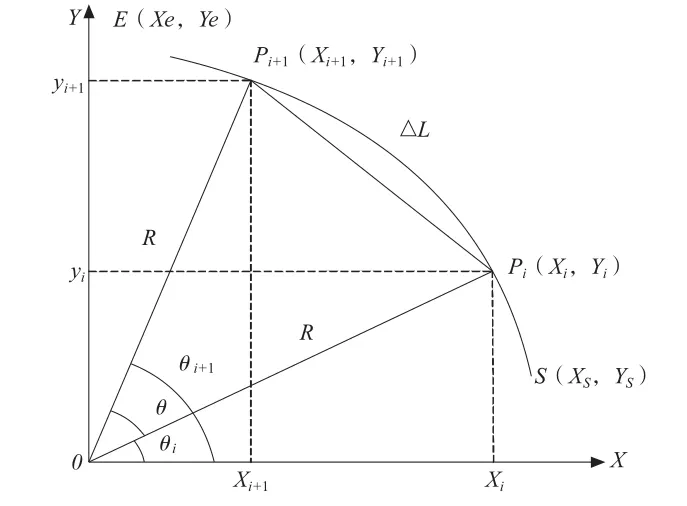
图2 圆弧粗插补示意图

设当前的插补周期为Ts(ms)，进给速度为F(mm/min)，以圆弧PiPi+1的弧长ΔL(μm)为进给量可得:

圆弧Pi Pi+1对应的圆心角θ(rad)为:

根据圆弧的参数方程有:

根据图2 和式(4)，下一插补点的参数方程为:

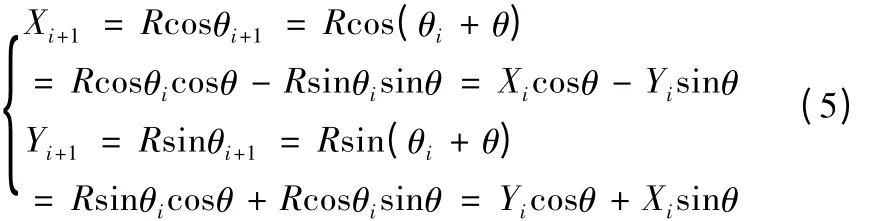
式(5)描述了下一插补点的坐标值该如何计算。通过式(3)算出θ，再带入式(5)即可求出下一插补点。

为避免硬件计算精度限制带来的累积误差，确保插补点始终落在圆弧上，算法采用如下计算规则来计算(Xi+1，Yi+1)。首先由Xi+1= Xicosθ- Yisinθ 计算出Xi+1，再由(6)计算出Yi+1:

式(6)中的Yi+1的正负可在算法中根据θ 的值判断。

各轴的位移量为:

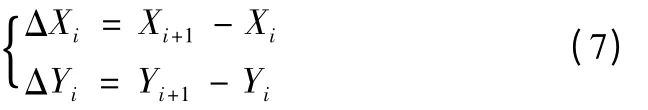
1.2 圆弧精插补

在圆弧精插补阶段，基于数字积分法，根据圆弧粗插补运算得到当前插补点坐标、下一插补点坐标和顺逆圆等信息，为各坐标轴分配脉冲，最终生成圆弧轨迹。

数字积分法的基本思想，就是把插补看作是插补点在各坐标轴分量分别累积的过程。坐标值应该每经过一个时间间隔，累积一个单位位移。每个坐标轴分别分配一个由余数寄存器和被积函数寄存器组成的积分器。每经过一个时间间隔，余数寄存器的值就与被积函数寄存器的值累加，当余数寄存器溢出就发出一个进给脉冲，否则，继续累加，并把余数保存在余数寄存器。

传统的数字积分法的主要缺点是累加过程的时钟频率固定。确定寄存器位数后，都要经过固定次数的累加运算才能完成插补运算，无论目标轨迹长短。所以进给时间不可改变。即目标轨迹越长，插补速度越快，反之亦然。传统数字积分法的另一缺点是造成各坐标轴在小线段衔接处进给速度的突变［1］。

通过速度规划算法生成速度变化平稳的轨迹，具体过程如下:①获得每个粗插补周期的进给率。②对精插补模块的时钟频率进行分频，即改变在数字积分法中的时钟频率。经过如上所述的处理，虽然目标曲线长度不一样时积分器的累加次数固定不变，但累加的快慢改变，累加运算的时间改变。累加运算的时间决定了进给速度，即通过变频实现了数字积分法的速度控制。

设脉冲当量为δ(mm)，则进给速度F转换成进给脉冲的频率为f(Hz):

设硬件精插补模块的时钟源的频率为f_origin(MHz)，则其分频系数divider_origin与进给脉冲的频率f(Hz)的关系如式(9):

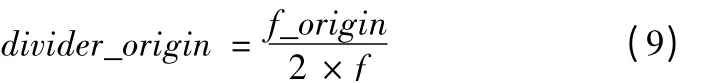
通过过象限处理实现任意弧长(包括微小圆弧、近似整圆或整圆)、任意象限的圆弧精插补。过象限处理的基本思路，就是以(R，0)、(0，R)、(- R，0)和(0，-R)为分界点，把圆弧划分为四个象限，然后根据动点的坐标判断其所属象限，在不同象限根据不同的进给规律进行插补。把分界点看作跨象限圆弧跨象限前的临时终点。根据半径R和坐标值的大小关系判断动点是否即将过象限，以分界点为临时终点控制各轴积分器启停。

为了对坐标轴上的点进行统一处理，算法对“象限”进行重新定义。非坐标轴上的点，象限的定义不变;坐标轴上的点，象限的定义为下一插补点所属象限。算法对坐标点所属象限定义如表1 所示:

表1 坐标点所属象限

对于圆弧精插补，X轴和Y轴的被积函数寄存器分别存储Y轴和X轴的动点坐标值的绝对值。只要在插补过程中计算出动点的坐标值，即可根据表1 判断动点所属象限，然后根据表2 的规律得出进给方向，并在动点坐标变化时，修正被积函数寄存器的值。

在圆弧精插补过程中，X轴坐标值累积过程中的溢出脉冲被当作Y轴的进给脉冲，反之亦然。基于数字积分法的圆弧精插补，在X轴和Y轴不是同时到达终点，所以两轴都要进行终点判别，只有两轴都到达终点才认为到达终点。判别条件如式(10)所示:

式中JX和JY分别是X坐标和Y坐标进给脉冲总数。

圆弧精插补的流程如图3 所示。其中JVX 和JVY分别代表X轴和Y轴被积函数寄存器，JRX 和JRY 分别代表X轴和Y轴余数寄存器。

图3 圆弧精插补流程图

2 算法的MATLAB 仿真

不失一般性，设整圆的起点坐标S和终点坐标E是同一个点。在X-Y平面的坐标为(1.200，1.600)，单位为mm。脉冲当量为1 μm，粗插补的插补周期Ts为1ms。

采用内接弦线逼近圆弧，即弦线逼近的两级圆弧插补算法(传统算法)时，若令er为圆弧粗插补允许的最大径向误差，R为圆弧半径，则进给步长应满足:

若er为10 μm，则ΔL≤400μm，且由式(2)可知F≤24000(mm/min)。若最大径向误差er减小到2 μm，则F≤10733(mm/min)。

进给速度F分别为 24000(mm/min) 和10733(mm/min)时，在MATLAB 中仿真的传统算法和本文的无直线逼近的两级圆弧插补算法(简称本文算法)的插补轨迹如图4 所示，进给速度F为24000(mm/min)时插补轨迹的局部放大图如图5 所示，传统算法和本文算法的圆弧插补的径向误差曲线如图6 所示。

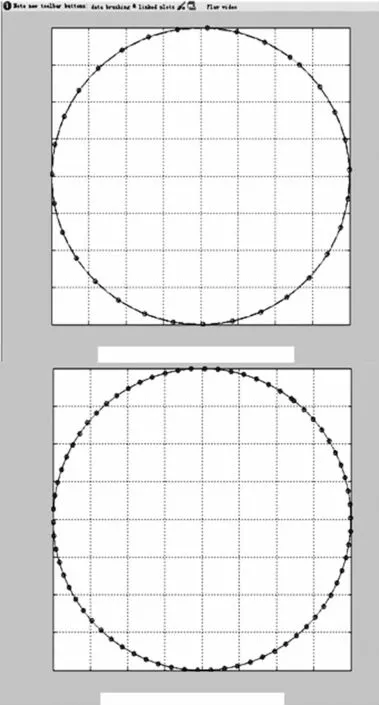
图4 不同进给速度的圆弧插补轨迹

图5 圆弧插补轨迹局部放大图

图6 不同进给速度的圆弧插补误差曲线

据图5 可知本文算法的粗插补的插补点比传统算法更加精确，插补轨迹更加接近给定圆弧轨迹;传统算法在直线段衔接处有速度波动，而本文算法没有。

据图6 可知，本文算法在进给速度改变时，径向误差不变;传统算法存在精度与效率的矛盾。这是因为本文设计的两级算法粗插补理论误差较小，插补精度仅由精插补的精度，即脉冲当量决定。所以对于本文算法可以提高进给速度或延长粗插补周期，而不影响插补精度。

3 无直线逼近的圆弧插补算法的实现

采用如图7 所示的基于DSP(数字信号处理器)+FPGA(现场可编程门阵列)的运动控制器实现本文设计的圆弧插补算法。该运动控制器架构如图7 所示，实物图如图8 所示。高速高精度的本文算法可在该运动控制器架构上实现:首先在DSP 上执行圆弧粗插补;然后将粗插补结果通过DSP 的XINTF(外部接口)接口将粗插补结果发送到FPGA;最后在FPGA 上执行圆弧精插补，并发送脉冲到伺服驱动器以驱动电机［5-7］。

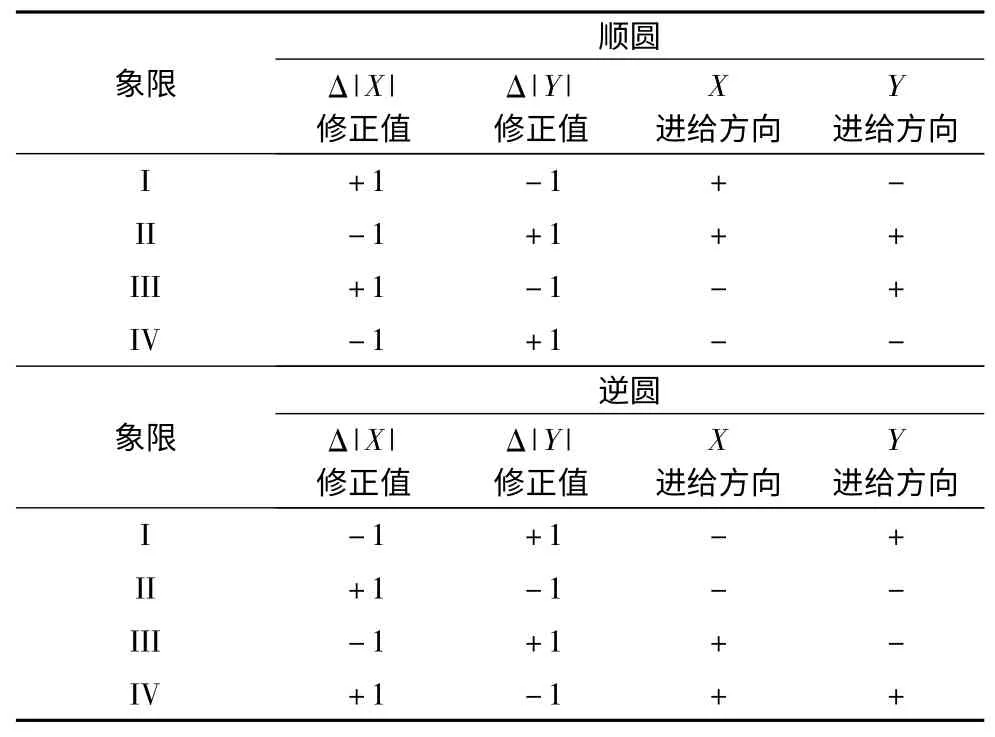
表2 进给方向及坐标绝对值变化规律

3.1 基于DSP 的软件粗插补

上述运动控制器中的DSP 采用32 位浮点数处理器—TMS320F28335，它专用于控制领域。在运动控制器中DSP 用于执行基于时间分割法的软件粗插补。

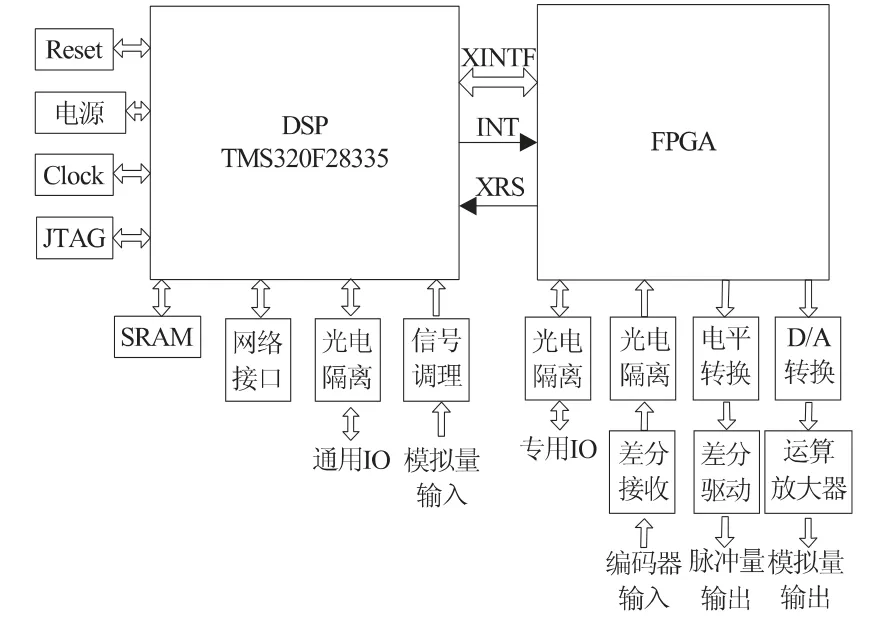
图7 基于DSP+FPGA 的运动控制器

图8 双轴运动控制实验平台

TMS320F28335 有着出色的三角函数运算能力，首先它有可进行三角函数运算的IQmath 运算库，其次它可通过查表法完成三角函数运算。这些都保证了插补运算的精度和实时性。为减少运算消耗，在编程中可先计算sinθ(或cosθ)，然后通过式(12)计算cosθ(或sinθ)

式(12)中的sinθ、cosθ 的正负可在程序中根据θ 的值判断。

圆弧粗插补通过以C 语言或汇编语言在集成开发环境CCSv3.3 中编写的DSP 程序的执行而实现。DSP 程序执行过程如下:

(1)在DSP 中将待插补平面圆弧通过坐标平移统一成圆心位于坐标原点的形式;

(2)根据平移后的圆弧起点坐标、终点坐标和进给方向等信息进行采用时间分割法，以弧长为进给量进行圆弧粗插补;

(3)圆弧粗插补的结果数据通过XINTF 接口把发送到FPGA。

3.2 基于FPGA 的硬件精插补

圆弧精插补通过以Vreilog HDL 语言在集成开发环境QuartusII 中编写的FPGA 程序的执行而实现。FPGA 根据圆弧粗插补结果采用数字积分法进行圆弧精插补，并把圆弧精插补的结果以脉冲的形式发送到伺服驱动器用于驱动电机，并通过XINTF 接口反馈状态信息到DSP，然后请求下一次圆弧精插补的数据。

采用Verilog HDL 语言实现基于数字积分法的硬件精插补模块分频。如前所述，分频模块式硬件精插补模块的子模块，它实现了数字积分发的运算速度控制。即分频模块使得所提出的算法实现了高速运动控制。FPGA 程序中的分频模块的部分源代码如下:

“clkin”代表FPGA 上来自晶振的初始时钟输入，且等于式(9)中的f_origin;divider_origin 等于式(9)中的divider_origin;“clkout”代表经过分频后的时钟输出;“rst”表示FPGA 复位，“en”表示精插补使能。

分频模块程序流程如图9 所示:

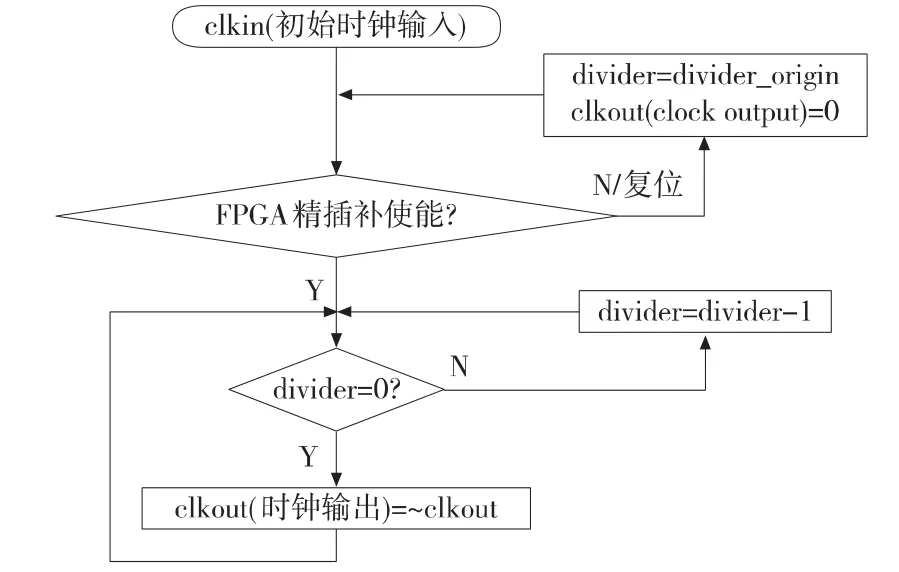
图9 分频模块程序流程

按照上述思路实现的本文算法可以控制运动平台插补出精确的目标曲线(平面圆弧)轨迹。

4 结论

在传统算法的粗插补阶段，逼近误差导致了运动速度与精度的矛盾。为实现高速高精度的运动控制，需要缩短插补周期，却又不能无限制的缩短。因为插补周期的大小由运动控制器的硬件性能限制。

在本文算法的粗插补阶段，以目标曲线的最大允许弧长为进给量，避免了线性逼近误差。所以本文算法的插补精度主要由精插补阶段决定。在满足插补精度的前提下，可增大进给率、延长插补周期，所以可实现高速高精度的运动控制。通过二维运动平台上的圆弧插补验证了本文算法的实用性。

无直线逼近的圆弧插补算法适合于复杂曲线、大曲率圆弧的高速高精度运动控制;无直线逼近的思路可以推广到更复杂的曲线插补。

［1］Jinho Park，Sungho Nam and Minyang Yang，Development of a realtime trajectory generator for NURBS interpolation based on the two stage interpolation method，Int J Adv Manuf Technol，26(2005):359 -365.

［2］X. Zhiming，C. Jincheng and F. Zhengjin，Performance Evaluation of a Real-Time Interpolation Algorithm for NURBS Curves，Int J Adv Manuf Technol，20(2002):270 -276.

［3］刘宜，丛爽，钱炜，等.一种基于时间分割法和数字积分法混合实现的空间直线插补方法［J］.机械设计，2008(25)12:27 -30.

［4］罗良玲，刘旭波. 基于时间分割法的圆柱螺旋线直接插补算法［J］.南昌大学学报，2001(23)4:57 -59.

［5］J. B. Huang，Z. W. Xie，H. Liu，K. Sun，Y. C. Liu and Z. N. Jiang，DSP/FPGA-based Controller Architecture for Flexible Joint Robot with Enhanced Impedance Performance，J Intell Robot Syst，53(2008):247 -261.

［6］Bin Yao，Mohammed Al-Majed and Masayoshi Tomizuka，High-Performance Robust Motion Control of Machine Tools:An Adaptive Robust Control Approach and Comparative Experiments，IEEE/ASME Trans. Mechatron，2 (1997):63 -76.

［7］HO Seong Lee and Masayoshi Tomizuka，Robust Motion Controller Design for High-accuracy Positioning Systems，IEEE TRANSACTIONS ON INDUSTRIAL ELECTRONICS，43(1996):48 -55.

［8］ TI Corporation， TMS320F28335， TMS320F28334，TMS320F28332， TMS320F28235， TMS320F28234，TMS320F28232 Digital Signal Controllers (DSCs)，The technology document of TI Company，2007.

［9］Hua Qiu，Kai Cheng and Yan Li，Optimal circular arc interpolation for NC tool path generation in curve contour manufacturing，Computer-Aided Design，29(1997):751 -760.

［10］Michael D. Ciletti ，Advanced Digital Design with the Verilog(TM)HDL，Prentice Hall，Upper Saddle River，NJ;2002.