切削颤振综合预报函数的构建研究*
徐志明,贺 勇,孙 涛,李国平
(宁波大学 机械工程与力学学院,浙江 宁波 315200)
0 引言
切削颤振[1]是一种典型的自激振动现象,是“机床-刀具-工件”构成的闭环切削系统的动态不稳定现象,根源于切削力的异常变化。它会造成刀具与工件之间十分强烈而持续的相对振动,从而影响零件的加工质量,大大降低切削加工的质量和效率,严重时会破坏被加工零件,出现崩刃、加工中断等后果,甚至会对机床产生较大的冲击力。自从1907 年美国学者F.W. Taylor 发表第一篇有关切削颤振的文章以来[2],人们在机床切削颤振领域做了大量的研究,主要目的是通过在线监测切削加工过程,判别切削颤振发生的征兆,然后通过减振措施抑制颤振的进一步发展。在这些研究工作中,如何建立一个快速准确的预报函数来判别切削颤振发生的征兆,对切削颤振的快速抑制十分重要。
切削颤振预报函数是基于机床切削过程中从稳定切削过渡到颤振切削的信号特征建立的识别此过程的函数。Rioulo 等提出了将不同的时频能量信号作为切削颤振特征量建立预报函数[3]。JongMin Lee 等人将隐马尔可夫模型应用于切削颤振的在线监测与判别,并且通过实验验证了切削颤振在线智能监测的预测性和准确性[4]。Taejun Choi 等运用小波参数估计法建立了一种不受切削条件影响的切削颤振参数识别法,这种参数估计法不仅具有很好的准确性和及时性,而且可以识别不同切削条件下颤振的发生[5]。吕凯波、景敏卿等自主开发了一种实用的切削颤振监测系统,通过监测数据与正常切削时建立的对比库进行对比从而对切削颤振进行预报研究,并通过了大量实际加工的验证[6]。胡耀斌、江涌涛等首先对切削振动信号进行小波包分解,然后对各频带区间内的能量进行归一化处理,最后通过SVR 算法对能量变化进行回归预测,预测结果基本可以反映出能量的变化趋势,从而预测切削颤振的发生[7]。康晶、冯长建利用自组织特征影射神经网络对提取的特征矢量进行与分类编码,然后基于离散隐马尔可夫模型的模式识别理论建立了一种切削颤振的概率识别方法,并实验验证了可行性[8]。
本文基于切削颤振信号的方差比和自相关函数的实验与仿真分析,提出一种以方差比和自相关函数为基础建立的切削颤振综合预报函数,通过实验验证它可以准确判别切削颤振的发生,避免偶然因素引起的过判和漏判。
1 切削颤振信号采集系统
切削颤振是刀具和零件之间的相互剧烈振动的现象,但是刀具与零件间的相对振动难以检测,所以切削颤振信号采集系统选取能够敏感反映切削状态变化的刀架振动加速度信号作为切削颤振的特征信号[9],并在一台最大加工直径为350mm 的C646 车床上进行颤振监测实验,采集系统组成如图1 所示。
图1 中标号1 的器件是型号为8640A50 的KISTLER 加速度传感器,可以获取主切削方向上刀架的振动加速度,驱动电源与信号放大器采用配套的型号5134B 型一体电源与信号放大器,频谱分析仪选用型号CF-7200FFT 幅频分析仪,实时观测振动信号,信号采集器运用USB 接口实时将幅频分析仪采集到的数据输入电脑。图2a,2b 为稳定切削和颤振切削的典型振动信号。

图2 稳定切削与颤振切削的振动信号
2 以切削振动信号的方差比构建颤振预报函数
从图2 可以看出,切削过程从稳定切削到颤振切削的发展过程中,时域内的切削振动信号幅值迅速增大。信号方差可以有效反映信号幅值增大过程,所以信号方差可以作为切削颤振发生的特征量,其计算公式为:
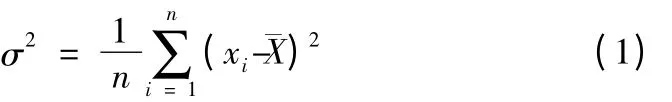
式(1)中,xi为振动信号,n为样本容量,为平稳切削的振动信号平均值
运用Matlab 软件中的函数功能求解振动信号方差,每隔128 个点确定一个样本,求得图2 所示两种典型切削振动信号的样本方差,样本方差的变化过程如图3 所示。
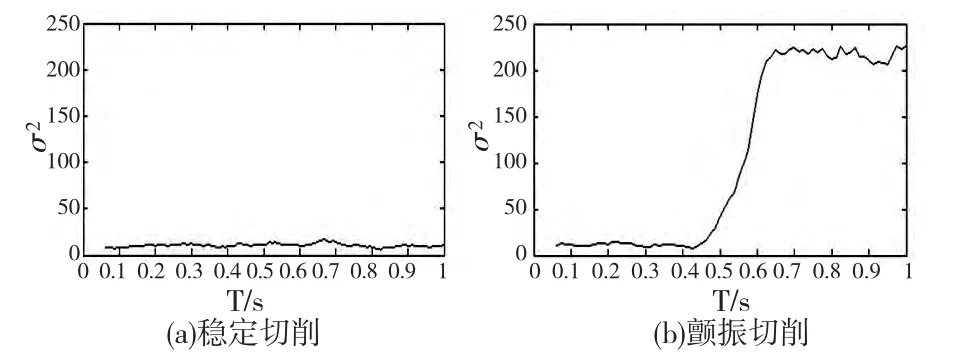
图3 稳定切削与颤振切削的信号方差
由图3b 可以看出,切削颤振发生时振动信号方差σ2随振动幅值增大而增大,有效反映了振动信号的幅值增大过程。但是在不同的加工条件下,切削力大小相差很大,导致稳定切削时切削振动信号的幅值也相差很大,甚至有时大切深稳定切削时的振动幅值会大于小切深颤振切削时的振动幅值,因此单独以方差σ2构建预报函数难以确定切削颤振的判别阀值。而方差比是一个可以反映振动信号瞬时幅值相对于稳定幅值(平均幅值)增长情况的无量纲数,可以消除稳定切削的振动信号幅值变化对颤振预报函数预判阀值的影响,所以改进以方差比建立切削颤振预报函数,定义为:


图4 颤振切削的信号方差比
对比图4 和图3b 可以看出,切削振动信号的方差比对幅值变化更加敏感,特别是颤振初期方差比的增长速度明显比方差快(即0.4s~0.5s),而且它是一个无量纲数,消除了不同切削条件下的稳定切削振动变化对颤振预报函数预判阀值的影响,所以方差比更适合作为判别切削颤振发生的时域特征量。
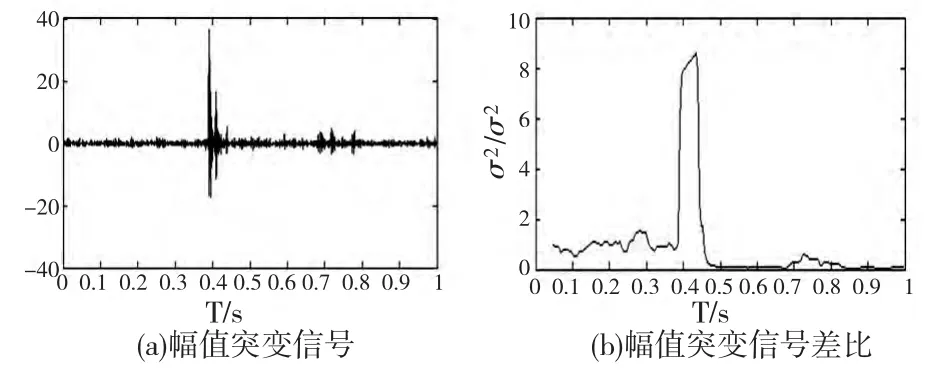
图5 偶然因素产生的突变信号及其方差比
但是在实际稳定切削过程中由于一些偶然扰动因素的影响,时域内振动信号的幅值会产生突变,如图5a 所示,这种情况会造成信号方差比也产生突变,如图5b 所示。这种情况下,单独以切削振动信号的方差比构建颤振预报函数会产生误判,所以虽然切削振动信号的方差比可以反映切削颤振产生过程的时域幅值特征变化,但是单独以信号方差比Bσ作为特征量建立的切削颤振预报函数,在预报切削颤振时不能取得很好的预测效果。
3 以切削振动信号的自相关函数构建颤振预报函数
振动信号的方差比是按照样本的时间顺序计算,而它的大小不受时间顺序的影响。信号的自相关特性可以反映信号中两个不同时刻状态之间的关系[10]。因此,对颤振信号进行自相关性分析可以得到切削颤振发生时的振动信号频率特征。
自相关函数是反映信号自相关特性的特征量,设振动信号两个不同时刻的时间差为Δ,则自相关函数可表示为:
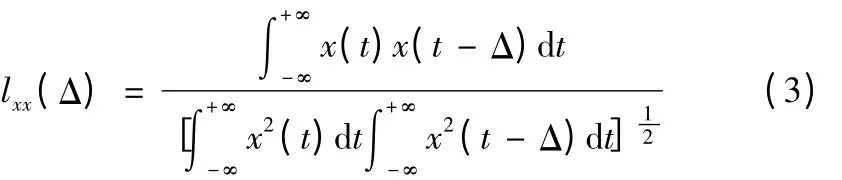
为了分析自相关函数lxx(Δ)与信号频率的关系。首先考虑信号由单一谐波信号组成:

观察自相关函数与信号频率的关系,取值An =10,bn取方差为1、均值为0 的白噪声,信号频率an =n(n=1,2,3,…,6400),采样频率取f =3200 Hz,总样本容量N=6400,所得的信号如图6a 所示。每隔128个点确定一个小样本,计算每一个小样本的自相关函数lxx(Δ),得到计算结果如图6b 所示。

图6 取样信号频率和自相关函数的周期关系
由图6b 可以看出,自相关函数是信号频率的周期函数,周期是为取样频率。当信号频率在信号频率在1600Hz 内,即信号频率在取样频率内时,自相关函数lxx(Δ)与信号频率an之间为递减关系,而在工程采样中,为了获取全部采样信号的所有信息,采样频率一般至少取信号频率两倍。现在只考虑采样频率大于两倍信号频率的情况,如图7 所示。

图7 信号的自相关函数
由图7 可以看出,当采样频率大于两倍信号频率时,单一波形信号的自相关函数与信号频率之间有确定的递减关系。而在实际工程测试信号往往含有各种频率成分,所以再假定振动信号包含有m种谐波成分
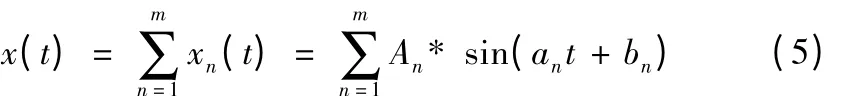
在多谐波信号的情况下,运用Matlab 软件分析切削振动信号自相函数lxx(Δ)与信号主能量频率之间的关系,用两个余弦波模拟多个谐波中的两个主能量频率信号,用白噪声模拟其他谐波,则信号可以表示为

用两个余弦波的幅值变化模拟多谐波信号不同频率信号的能量变化引起的信号主能量频率改变,即信号主能量的频率变化,观察多谐波信号的自相函数lxx(Δ)随多谐波信号主能量频率的变化情况,如图8a,8b,8c 所示。
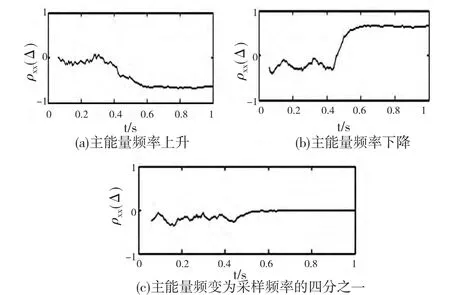
图8 信号自相关函数lxx(Δ)与主能量频率的关系
第一种情况,如图8a 所示,当信号主能量频率从600Hz 转移到1000Hz 时,信号自相关函数lxx(Δ)随信号主能量频率增大而逐渐变小;第二种情况,如图8b所示,当信号主能量频带从600Hz 转移到200Hz 时,信号自相关函数lxx(Δ)随信号主能量频率减小而逐渐增大;从上两种情况可以看出,多谐波信号的主能量频率与自相关函数lxx(Δ)与具有确定反向关系。第三种情况,如图8c 所示,当信号的主能量频率靠近采样频率的四分之一时,信号自相关函数lxx(Δ)趋向于零,此时信号自相关函数lxx(Δ)随信号频率的变化的趋势不明显,即当信号的主能量频率在采样频率的附近变化时,信号自相关函数lxx(Δ)不能很好地反映信号主能量频率的变化。
振动信号的自相关函数lxx(Δ)与主能量频率之间具有确定的反向关系,这给我们提供了一个可以反映振动信号频域特性的特征量。但是当信号的主能量频率在采样频率的附近变化时,信号自相关函数lxx(Δ)总会趋向于零,不能很好地反映信号主能量频率的变化,而且信号自相关函数lxx(Δ)也不能识别由于偶然因素引起的信号频率突变,这也使得单独以信号自相关函数lxx(Δ)建立的切削颤振预报函数,在预报切削颤振时也不能取得很好的预测效果。
4 综合预报函数的实验研究
单独以方差比Bσ或者自相关函数llxx(Δ)为特征量建立切削颤振函数时,都会受到一些偶然因素的影响,从而产生误判。因此,综合预报函数需要综合利用能反映切削颤振信号时域特征的方差比Bσ和频域特征的自相关函数lxx(Δ)。首先,利用符号函数sgn1(Bσ-K)简化时域特征量Bσ的取值,其中K相当于时域内的切削颤振阀值,当Bσ-K≥0 时,符号函数sgn1(Bσ-K)=1 ,反之,符号函数sgn1(Bσ-K)= -1 。根据大量的实验研究,K取2.5 可以及时判别出时域内切削颤振的发生[9]。其次,虽然信号自相关函数lxx(Δ)可以反映信号主能量频率的变化,但是不同的切削条件自相关函数lxx(Δ)的取值范围不同,所以在建立切削颤振的频域特征函数时,可以选用统计量的置信区间来判断切削颤振频特征在频域内的变化,参考文献[11]取置信区间为±3σl,同样用符号函数来判断信号频域特征是否在置信区间内。其中l为瞬时自相关函数值lxx(Δ),为切削系统在稳定切削状态下计算的大量瞬时自相关函数值lxx(Δ)的平均值,σ2ell为切削系统在稳定切削状态下计算的大量瞬时自相关函数值lxx(Δ)的方差。当l --时,符号函数,反之,符号函数;最后将两个符号函数以2 的指数形式转化到正值域,并将它们相乘建立切削振动信号的方差比和自相关函数的综合预报函数,其定义为:
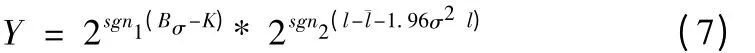
因此综合预报函数就简化为一个0.25、1 和4 的阶梯函数,当稳定切削时,方差比Bσ比较小,则Bσ-K<0 ,时域特征量2sgn1(Bσ-K)=0.5 ,同时信号的主频带比较稳定,则自相关函数lxx(Δ)在置信区间内,则频域特征量2sgn2(l-¯l-1.96σl)=0.5 ,则预报函数值为Y =0.25 ;如果由于偶然因素导致系统振动突然幅值增加,则可能会导致Bσ-K≥0 ,时域特征量2sgn1(Bσ-K)=2 ,然而只要频域特征量不受影响,仍然为0.5,预报函数值B =1 ,另外对于偶然因素导致系统频率突变也是一样,只要时域特征量和频域特征量不同时变化,预报函数值最大为1;当发生切削颤振时,时域内振动幅值肯定会迅速增大,从而使Bσ-K >0 ,频域特征量增大到2,频域内颤振信号的主能量频率会从高频段向低频段转移,而由前面分析可得信号自相关函数lxx(Δ)会随之变大,从而使得自相关函数lxx(Δ)超出置信区间,则l --1.96σ2l >0 ,频域特征量增大到2,这时预报函数值为4,所以综合预报函数值为:

为了验证综合预报函数的颤振预报性能,将采集的切削颤振信号作为综合预报函数的输入值,输出预报函数判别值。如图9a 和图9b 所示分别为部分振动加速度信号和综合预报函数的判别值。
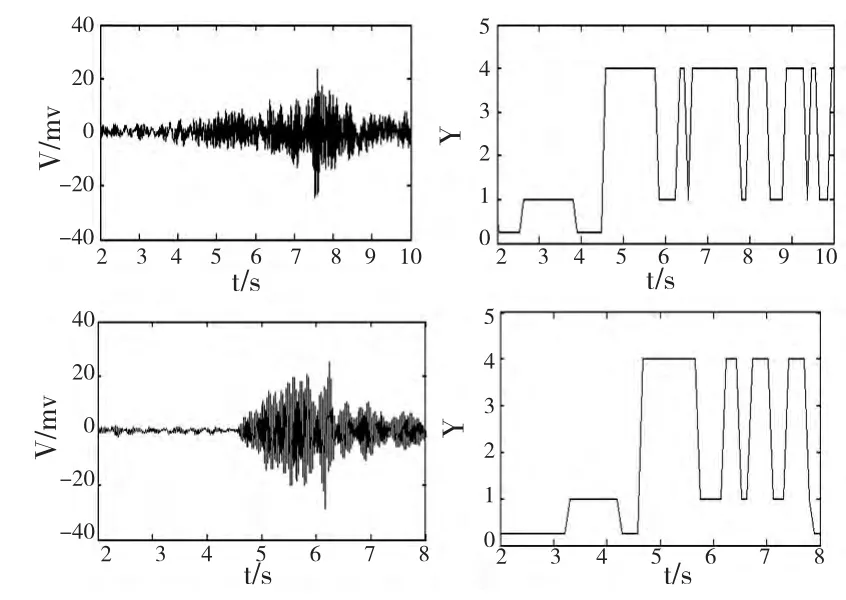
图9 综合预报函数的实验结果
对比图9a 和图9b 可以看出,以方差比和自相关函数建立综合预报函数可以准确判别切削颤振的发生,减少偶然因素引起的误判。
5 结论
(1)研究表明方差比和自相关函数能分别反映切削颤振发生时的时域征兆和频域征兆,但是单独以一个特征量建立切削颤振预报函数,都难以排出偶然因素引起振动幅值或者信号频率突变造成的过判和漏判。
(2)本文以切削振动信号的方差比和自相关函数为基础,定义了一个综合利用切削振动信号的方差比和自相关函数的阶梯函数作为切削颤振综合预报函数,并通过实验结果证明它可以准确判别切削颤振的发生,减少偶然因素引起的过判和漏判。
[1]唐英,张大勇. 切削颤振研究的关键技术与进展综述[J].工具技术,2011,45(8):9 -14.
[2]F.W. Taylor . On the Art of Cutting Metals[M]. ASME,1907.
[3]Rioulo,Flandrin P . Time-scale energy distributions:a general class extending wavelet transforms[J]. IEEE Transaction on Signal Processing,1992,40(10):1746 -1757.
[4]Jong Min Lee,Seung Jong Kim et al. Diagnosis of meehanica1 fault signa1 using continuous Hidden Markov model[J].Journal of Sound and Vibration,2004,276:1065 -1080.
[5]Taejun Choi,Yung C Shin. On-line chatter detection using wavelet-based parameter estimation. Journal of Manufacturing Science and Engineering,2003,125(2):21 -28.
[6]吕凯波,景敏卿,张永强,等.一种切削颤振测试技术的研究与实现[J].西安交通大学学报,2011,11(45):95 -99.
[7]胡耀斌,江涌涛,张春良,等.基于支持向量回归的切削颤振状态趋势预测的研究[J]. 组合机床与自动化加工技术,2006(3):42 -46.
[8]康晶,冯长健,杨国田.离散隐马尔可夫模型在颤振预报中的应用研究[J].机械科学与技术,2008,27(3):360-364.
[9]师汉民.金属切削理论及其应用新探[M].武汉:华中科技出版社,2003.
[10]程桂芳.随机信号处理与控制基础[M].北京:化学工业出版社,2002.
[11]于骏一,周晓勤.切削颤振的预报控制[J].中国机械工程,1999,9(10):1028 -1032.

