型钢混凝土立柱与斜柱汇交节点有限元分析

谢移爱 徐其功 郑美如

(广东省建科建筑设计院，广州510640)

1 引言

混凝土结构中梁柱节点受力复杂，对整体结构的安全起着至关重要的作用。近年来，对型钢混凝土梁柱常规节点及非常规节点的性能有较多的研究[1，2]，但目前尚没可以验证型钢混凝土节点承载能力的相关规范和计算公式。一般都是对具体工程的节点进行试验及有限元工具对比分析研究。采用有限元分析软件ABAQUS进行仿真模拟，其提供的混凝土塑性损伤模型具有较好的收敛性，可较好地描述混凝土破碎过程中不可恢复的塑性损伤性能[3]，且其具备丰富的单元库和材料模型库，具有强大的分析能力和模拟功能，能够准确的模拟材料的受力性能[4]。

对于ABAQUS有限元软件的应用，黄超和韩小雷[5]等通过该软件对竖向荷载下钢管混凝土平面相贯节点进行计算分析，得出节点的破坏形态和承载能力计算公式。王琨和袁沈峰[6]对型钢混凝土梁-角钢混凝土柱框架采用三维实体建模，能较为真实地模拟框架的受力过程。文献[7]对框架顶层端节点建立模型，对其性能进行了有限元分析，得出了顶层端节点的受力机理等。

目前，对于立柱与斜柱汇交节点的研究较少，此类节点构造、受力较为特殊，多个构件作为受力体，其中斜柱承受较大轴力，因此在设计时采用型钢混凝土柱有利于控制截面面积，同时增加汇交节点延性。为了模拟节点在实际荷载工况下的承载性能，进一步研究该节点的极限承载能力，文中采用ABAQUS有限元软件对广东商学院图书馆型钢混凝土立柱与斜柱汇交节点进行数值模拟分析。

2 工程概述

广东商学院图书馆是集行政办公、校园信息数据中心、校史展览馆、报告厅为一体的综合性建筑，总建筑面积为32 020 m2，共8层，位于新校区的核心位置，正对校门广场，矗立珠江边，是将来新旧校区最重要的地标式建筑，工程效果图如图1所示。裙楼1层，主楼7层，建筑体型上大下小，结构形式复杂，采用框架-抗震墙结构体系(图2)，属于平面及竖向特别不规则的复杂高层建筑。建筑四周由斜柱作为主要受力构件，在二层形成汇交节点，角节点由立柱与三根斜柱组成，边节点由立柱与一根斜柱组成，立柱与斜柱均采用型钢混凝土柱。

图1 建筑形态Fig.1 Architectural form

图2 结构计算模型简图Fig.2 Diagram of structure calculation model

本文根据柱子的外形尺寸和周边构件的关系，在角节点处选取立柱、斜柱及剪力墙作为组合截面进行分析，斜柱与立柱的夹角为22°(图3)。混凝土强度等级C40，内置钢管材质为Q235，纵筋为HRB400，箍筋为 HPB300。立柱钢管截面D=500 mm，t=18 mm;斜柱钢管截面 D=350 mm，t=14 mm。

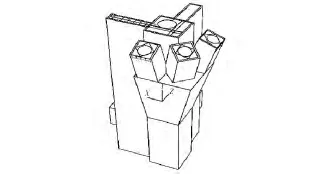
图3 角节点构造示意图Fig.3 Diagram of corner node details

3 有限元模型的建立

3.1 混凝土塑性损伤模型

ABAQUS自带三种混凝土本构模型:塑性损伤模型、弥散裂缝模型和开裂模型，本文采用塑性损伤模型，此模型假定混凝土材料主要因拉伸开裂和压缩破碎而破坏，与之对应的屈服或破坏面的形成分别由等效塑性拉应变和等效塑性压应变控制[4]。混凝土的应力—应变曲线方程通过《混凝土结构设计规范》(GB 50010—2010)规范推荐的公式确定，曲线如图4、图5所示。

图4 混凝土单轴受压应力应变曲线Fig.4 Stress-strain curve of concrete under uniaxial compressive

图5 混凝土单轴受拉应力应变曲线Fig.5 Stress-strain curve of concrete under uniaxial tension

损伤发生后混凝土单轴受压的应力—应变曲线方程可按下列公式确定:

损伤发生后混凝土单轴受拉的应力—应变曲线方程可按下列公式确定:式中为混凝土混凝土棱柱体试件达到轴心抗拉强度 ft所对应的应变，ξt，p=65 ×10－6

3.2 混凝土损伤因子

塑性损伤模型中，材料刚度损伤程度以受拉损伤因子和受压损伤因子来体现，其值为0～1，其值与混凝土受压、受拉应力-应变曲线成一一对应关系[5-7]，在混凝土受拉、受压弹性阶段时，相应的损伤因子D为0，认为没有损伤，在曲线峰值以后，损伤因子增大，当D=1时，为完全损伤。

单轴受压损伤方程:

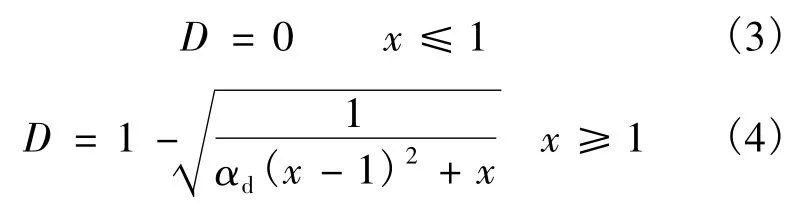
单轴受拉损伤方程:

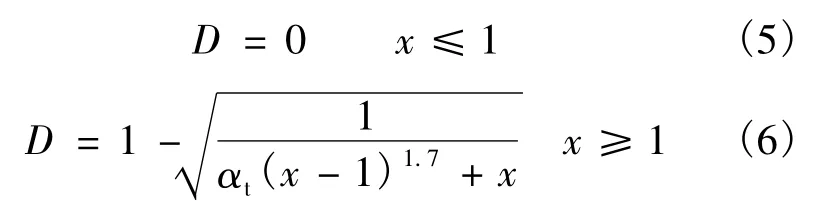
3.3 混凝土其他参数

ABAQUS/CAE中对混凝土损伤塑性模型需要定义相关的参数，包括流动势偏移值ε=0.1、膨胀角ψ=32°、黏性修正系数 μ=0.001、双轴极限抗压强度与单轴极限抗压强度比αf=1.16、拉伸子午面上和压缩子午面上的第二应力不变量之比Kc=2/3。

3.4 钢材本构模型

钢材应力—应变关系曲线采用双线性模型，利用ABAQUS提供的等向弹塑性模型，满足Von Mises屈服准则。即当钢材的等效应力超过屈服应力，钢材将发生塑性变形。

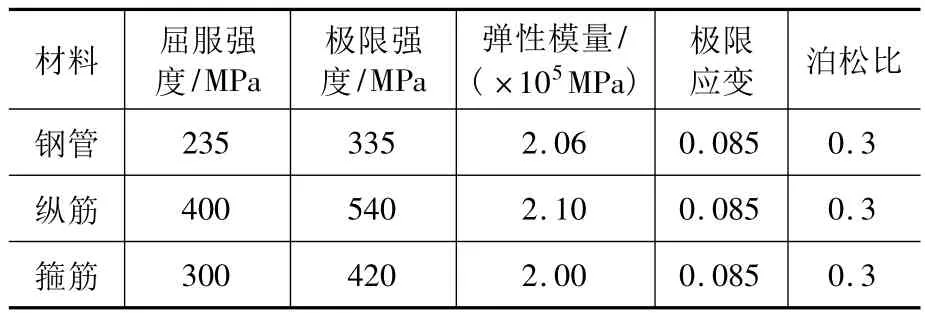
表1 钢材材料参数Table 1 Parameters of steel material

3.5 单元选择、接触定义及网格划分

混凝土采用8节点六面体线性减缩积分单元C3D8R和4节点四面体线性单元C3D4模拟;钢管采用4节点四边形有限薄膜应变线性减缩积分壳单元S4R模拟;钢筋采用三维2节点线性桁架单元T3D2来模拟。

模型中不考虑钢管与混凝土之间的滑移，在装配模型中将斜柱和立柱的钢管合并，混凝土部分合并。通过ABAQUS中的Embed命令将钢管镶嵌在混凝土中，钢筋单元同样使用Embed命令嵌入混凝土，剪力墙与柱子采用Tie连接，加载参考点与柱面及墙面采用Coupling进行耦合连接。有限元网格划分如图6所示。

3.6 加载方法

模型采用力加载方式，分两个模型进行计算分析，第一个是施加工程设计荷载，表2为从整体模型中提取的节点内力荷载，采用不利荷载组合1.2×恒载 +1.4×活载，轴力拉为正，压为负，立柱及剪力墙数值为总体坐标下荷载，斜柱荷载亦转换为总体坐标下荷载，总体坐标系见图6(a)，第二个是采用比例加载的方式，沿立柱及斜柱杆件轴向施加压力，计算至节点失效状态。

表2 节点内力计算结果Table 2 Result of internal forces calculation

4 数值模拟结果与分析

4.1 工程设计荷载工况

从钢筋混凝土塑性损伤模型的数值模拟中，得到立柱与斜柱汇交节点在不利荷载组合工况下的混凝土、钢筋和钢管的Von Mises应力如图7所示。

由图7(a)可看出整体混凝土最大Mises应力出现在剪力墙支座处，此处应力集中。其余位置应力均在20 MPa以下，应力分布均匀，未出现损伤的情况。整体上分析节点核心区应力较剪力墙小，因此节点有较高的安全储备。且节点处于弹性工作状态，满足规范要求。

由图7(b)得到柱混凝土切片的应力分布状态，斜柱与节点区交接的斜坡应力较大，最大Mises应力出现在一点上，为31.69 MPa，其余位置应力均在20 MPa以下，应力分布均匀，未出现损伤的情况。此外，立柱与斜柱汇交处的应力较小，由此可见，斜柱承担较大的荷载，可满足“更强节点”的要求。

通过图7(c)钢筋应力云图发现，立柱与斜柱钢筋应力较小，无屈服现象。剪力墙上部箍筋局部应力偏大，此处可适当增加配箍率。

通过图7(d)钢管应力云图可知，钢管最大主应力为107.5 MPa。应力处于较低水准，远小于Q235钢材的屈服强度235 MPa。

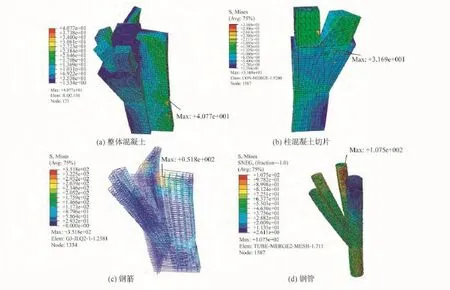
图7 应力云图Fig.7 Mises stress

4.2 极限承载力工况

图8为立柱和斜柱汇交节点有限元模型的荷载—位移关系，此位移为节点中截面相对支座的位移值。从图中可以看出立柱与斜柱加载前期，位移较小，为0.001～1 mm数值范围，当立柱荷载达到5 000 kN，斜柱荷载6 200 kN时，柱子位移缓慢增加，在破坏之前有明显的变形，荷载—位移曲线到达顶点之后有，位移增大，而承载力没有显著降低，属于延性破坏。立柱与斜柱的极限承载力分别为12 000 kN和10 000 kN，该节点有较富余的安全储备。

图9为节点在屈服荷载和峰值荷载时，钢管、混凝土、钢筋的节点Mises应力分布状态，从图中可以看出，在屈服荷载时，核心区混凝土形成带状受压区域，部分核心区混凝土出现刚度退化，但对应的核心区型钢管应力较小、均小于130 MPa，处于弹性状态;斜柱中的钢管、钢筋局部屈服，表明在加载过程中立柱先破坏，核心区后破坏。到极限荷载时，钢管、钢筋屈服，混凝土受压破坏。

图8 荷载—位移曲线Fig.8 Load-displacement curve

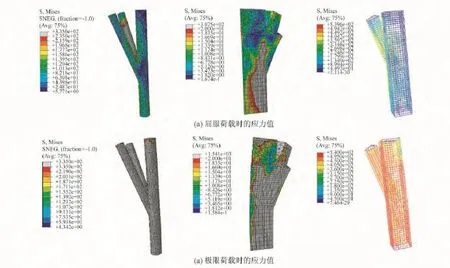
图9 应力分布Fig.9 Stress distribution

5 结论

综上所述，本文采用ABAQUS中的塑性损伤模型，引入恰当的材料本构及损伤因子，建立了立柱与斜柱汇交节点有限元模型，可以较好地模拟节点在实际荷载工况下的工作状态，通过计算分析处理，得出如下结论:

(1)在实际荷载工况下，此节点混凝土、钢筋应力均小于规范要求，未出现损伤和屈服的现象，处于弹性工作状态，符合规范要求。且总体应力分布均匀，设置经济合理，承载力较高。

(2)采用有限元方法对节点进行轴压承载力分析，得出立柱与斜柱的极限承载力分别为12 000 kN和10 000 kN，该节点有较富余的安全储备。

(3)此类型节点能满足结构设计的要求，并达到了强节点的性能目标，可为其他类似工程提供参考。

[1] 刘维亚.钢与混凝土组合结构理论与实践[M].北京:中国建筑工业出版社，2008.Liu Weiya.Theory and practice of steel and concretecomposite structure[M].Beijing:China Building Industry Press，2008.(in Chinese)

[2] 赵鸿铁.钢与混凝土组合结构[M].北京:科学出版社，2001.Zhao Hongtie.Steel and concrete composite structure[M].Beijing:Science Press，2001.(in Chinese)

[3] 张劲，王庆扬，胡守营，等.ABAQUS混凝土损伤塑性模型参数验证[J].建筑结构，2008，38(8):127-130.Zhang Jin，Wang Qingyang，Hu Shouying，et al.Parameters verification of concrete damaged plastic model of ABAQUS[J].Building Structure，2008，38(8):127-130.(in Chinese)

[4] Simulia.ABAQUS user’s manual，Version 6.8[R].2007.

[5] 黄超，韩小雷.钢管混凝土平面相贯节点轴压承载力理论研究[J].华南理工大学学报(自然科学版)，2010，38(7):128-134.Huang Chao，Han Xiaolei.Theoretical investigation into axial bearing capacity of planar intersecting connections of concrete-filled steel tube[J].Jourmal of South China University ofTechnology (Natural Science Edition)，2010，38(7):128-134.(in Chinese)

[6] 王琨，袁沈峰，郑文忠.水平荷载作用下型钢混凝土梁-角钢混凝土柱框架非线性有限元模拟[J].结构工程师，2011，27(6):41-47.Wang Kun，Yuan Shenfeng，Zheng Wenzhong.Nonlinear finite element simulation on a frame structure of steel reinforced concrete beam and angle steel concrete column under horizontal loading[J].Structural Engineers，2011，27(6):41-47.(in Chinese)

[7] 彭志桢，王智勤.基于ABAQUS的RC框架顶层端节点有限元分析[J].重庆交通大学学报(自然科学版)，2010，29(5):678-680.Peng Zhizhen，Wang Zhiqin.ABAQUS FEM analysis on knee joints in reinforced concrete frames[J].Journal of Chongqing Jiaotong University(Natural Science Edition)，2010，29(5):678-680.(in Chinese)

[8] Lubliner J，Oliver J，Oller S，et al.A plastic damage model for concrete[J].International Journal of Solid and Structures，1989，25(2):102-113.

[9] Lee J，Fenves G L.Plastic damage model for cyclic loading of concrete structures[J].Journal of Engineering Mechanics，1998，124(8):204-216.

[10] Hibbitt Karlson Sorenson. ABAQUS Version 6.7 Theory manual users manual verification manual and example problems manual.Hibbitt，Karlson and Sorenson Inc.，2007.