基于优化的GM(1,1)模型在高速公路沉降预报中的应用
张非非,胡 健,佘兆宇
(江苏现代路桥有限责任公司,江苏南京 210049)
基于优化的GM(1,1)模型在高速公路沉降预报中的应用
张非非∗,胡 健,佘兆宇
(江苏现代路桥有限责任公司,江苏南京 210049)
GM(1,1)模型是最常见的灰色系统模型,也是预测理论体系中的一个重要分支,被广泛应用于各种建筑物、构造物的变形监测预报中。本文针对传统GM(1,1)模型中存在的问题,对模型中的初始值、背景值及时间响应函数进行优化,得到一个优化的GM(1,1)模型,并将其应用到高速公路的沉降预报。实例证实,优化的GM(1,1)模型的模拟和预报精度比传统GM(1,1)模型有显著提高,体现了该模型的优良性与适用性。
GM(1,1)模型;初始值;背景值;时间响应函数;沉降预报
1 引 言
在修建与维护高速公路中,沉降监测是判断路面高程变化及其平整度和稳定性的重要手段。沉降预报是沉降监测数据处理的重要组成部分,常用的沉降预报模型有回归分析、人工神经网络、时间序列分析、灰色系统模型等。其中,灰色系统模型能够根据少量已知信息进行建模和预报,且建模简单,预报精度高,被广泛地应用于各个领域中,GM(1,1)模型是最常用的灰色系统模型[1~3]。
传统GM(1,1)模型成功地应用到诸多工程的沉降预报中,但同时也出现一些预报精度不高的情况,所以有必要对GM(1,1)模型进行优化[4]。本文分析了传统GM(1,1)模型中存在的不足,对模型中的初始值、背景值及时间响应函数进行优化,构成优化的GM (1,1)模型。通过实例,将传统GM(1,1)模型和优化的GM(1,1)模型分别应用到高速公路的沉降预报中,并比较二者的预报精度。
2 传统GM(1,1)模型
2.1 建模步骤[5~7]
(1)给定原始观测序列,记为:
X(0)={x(0)(1),x(0)(2),…x(0)(n)}
(2)对上式进行一阶累加,生成1-AGO序列,记为: X(1)={x(1)(1),x(1)(2),…x(1)(n)},公式表示如下:
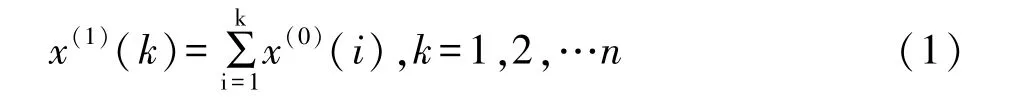
(3)进行准光滑性检验、准指数规律检验:


当ρ(k)<0.5且σ(1)(k)∈[1,1.5]时,则X(0)满足准光滑、准指数规律条件,可以使用GM(1,1)模型建模。
(4)生成紧邻均值序列,又称为背景值序列,记为:Z(1)={z(1)(1),z(1)(2),…z(1)(n),公式表示如下:

其中参数a反映了系统发展的态势,称为发展系数;b是反映数据变化的关系,称为灰色作用量。根据最小二乘原理,解该白化微分方程,可得到时间相应函数为:

(6)进行累减还原序列为:

2.2 模型精度评定
(1)计算模型残差:

(2)计算原始观测序列X(0)的均值¯x和方差:

(3)计算模型残差的均值¯ε和方差s22:

(4)计算后验方差比值c和小误差概率p:
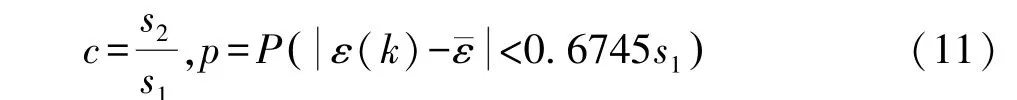
当后验方差比值c<0.35,且小误差概率p>0.95时,传统GM(1,1)模型的预报精度良好。
3 优化的GM(1,1)模型
当序列数据变化急剧(高增长指数情况)时,若直接采用传统GM(1,1)模型往往会产生较大滞后误差,模型偏差较大。近年来,很多学者从不同的方面进行GM(1,1)模型优化,来提高建模精度。本文提出对模型的初始值、背景值及时间响应函数进行优化并相结合的方法,得到优化的GM(1,1)模型。
优化的GM(1,1)模型的建模步骤如下:
(1)给定原始观测序列X(0);
(2)对上式进行一阶累加,生成1-AGO序列X(1);
(3)对模型的初始值进行优化,使X(1)所有分量的拟合误差平方和S最小,即:

则模型的初始值可优化为:

(4)生成优化的背景值序列Z(1):

其中,当x(0)(k)=x(0)(k-1)时,z(1)(k)=x(1)(k)。
(5)生成优化的时间相应函数:

4 实例计算
以连云港某段高速公路的修建和运营阶段的沉降观测为例,出于工程安全考虑,我们对其进行了长期沉降监测。在修建阶段(1期~40期)中,由于施工条件限制,观测数据浮动较大,变化急剧;而在运营阶段(41期~60期)中,观测数据浮动较小,监测点较为稳定。
采用Matlab软件建立传统GM(1,1)模型与优化的GM(1,1)模型算法,选取#J01监测点在修建阶段1期~35期与在运营阶段41期~55期的高程观测值为原始观测序列,分别采用传统GM(1,1)模型与优化的GM(1,1)模型预报36期~40期、56期~60期的高程值,并与实测序列进行对比分析。
由图1可知,对于高速公路修建阶段中,数据变化急剧,累计沉降达到90 mm,使用优化的GM(1,1)模型的高程值模拟和沉降预报效果均优于传统GM(1, 1)模型。由表1可知,在修建阶段中,使用优化的GM (1,1)模型有较好地可靠度和精度。

图1 #J01监测点的沉降预报(修建阶段)

表1 修建阶段两种模型沉降预报精度评价指标

表2 运营阶段两种模型沉降预报精度评价指标

图2 #J01监测点沉降预报(运营阶段)
由图2和表2可知,对于高速公路运营阶段中,数据较为平稳,累计沉降为6 mm,变形量较小,使用优化的GM(1,1)模型与传统GM(1,1)模型的高程值模拟和沉降预报效果均良好,二者可靠度和精度也相当。
5 结 语
本文通过传统GM(1,1)模型的研究,提出了对模型中的初始值、背景值及时间响应函数进行改进的优化的GM(1,1)模型,并将该模型应用到高速公路的沉降预报。实例结果表明,优化的GM(1,1)模型对于数据变化急剧的原始观测序列的模拟和预报具有较好地优良性和适用性,对于数据变化平稳的原始观测序列的模拟和预报精度则与传统GM(1,1)模型相当。
[1] 刘思峰,党耀国,方志耕.灰色系统理论及其应用[M].北京:科学出版社,2010.
[2] 陈刚,王波,邓哲.GM(1,1)模型在建筑物沉降预测中的应用及Matlab的实现[J].城市勘测,2011(1):107~109.
[3] 兰孝奇,严红萍,刘精攀.灰色系统预测模型在沉降监测中的应用[J].现代测绘,2006,29(1):24~26.
[4] 李伟,袁亚南,牛东晓.基于缓冲算子和时间响应函数优化灰色模型的中长期负荷预测[J].电力系统保护与控制,2011,39(10):59~63.
[5] 何霞,刘卫锋.一个基于背景值和初始条件优化的GM (1,1)模型[J].河南科学,2011,29(3):260~263.
[6] 郑雪琴,秦栋.系统优化的GM(1,1)模型在大坝位移预测中的应用[J].水电能源科学,2011,29(4):75~77.
[7] 何勇刚,周步祥.缓冲算子改进灰色模型在中长期负荷预测中的应用[J].四川电力技术,2007,30(2):5~7.
[8] 谢正文,胡汉华,胡毅夫.改进GM(1,1)模型在路基沉降预测中的应用[J].岩土力学,2005,26(10):227~230.
The Application of The Optimized GM(1,1)Model in Settlement Forecast of Express Highway
Zhang Feifei,Hu Jian,She Zhaoyu
(Jiangsu Modern Highway Bridge Co.Ltd,Nanjing 210049,China)
GM(1,1)mode is the most common content of grey system theory.And it is also an important branch of forecasting theories.The model is used to forecast the deformation of building widely.According to the problems of the traditional GM(1,1)model,the initial value,background value and time response sequence were optimized firstly.The optimized GM(1,1)model was applied to the settlement forecast of express highway.Through the example,the results show that the optimized GM(1,1)model has a very high fitting and prediction precision than the traditional model.
GM(1,1)model;initial value;background value;time response sequence;settlement forecast
2013—08—21
张非非(1974—),男,工程师,主要从事道路桥梁检测研究工作。

