与轻质弹簧有关问题的分析与讨论
张 黎
(中山市华侨中学 广东 中山 528400)
在物理教学中经常涉及到弹簧的问题,中学范围内一般都将弹簧视作轻质弹簧.参考资料中普遍这样说明:弹簧(或橡皮绳)——特点是形变量大,两端同时连接有物体的弹簧其形变恢复需要较长时间,在瞬时性问题中,其弹力的大小往往可看成不变.
如图1所示情景中,A和B质量相等,系统处于静止状态,则弹簧弹力F=G,其中G为A或B的重力.若突然剪断细线瞬间,认为弹簧弹力不变,A所受的合力为F+G,B的合力为零,显然aA=2g,aB=0.
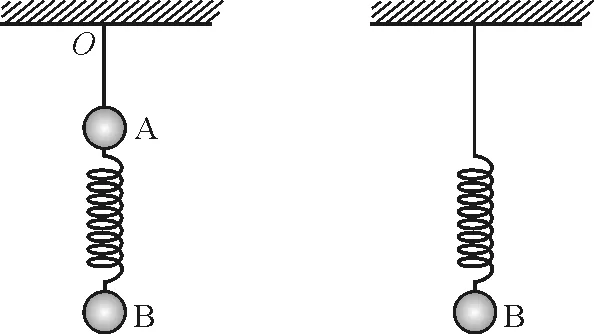
图1 图2
但是会有人提出第二种情景.如图2所示,细线连接弹簧,系统静止,那么剪断细线瞬间,B的受力情况如何呢?由于此时已不符合“两端同时连接有物体的弹簧”了,如果依然套用前面的思路,则弹簧对B的拉力为F,方向竖直向上,而弹簧上端弹簧拉力依然存在,方向竖直向下,但这个力没有受力物体,显然不符合力的三要素要求.那么这种情景弹簧两端的弹力究竟是多少?该如何处理此类疑问?以下提出一种解释方案.
1 轻质弹簧问题
高中物理课本中出现过轻质弹簧的概念.在“弹簧振子”模型中,如果弹簧质量比小球质量小得多,则可以视为轻质弹簧.所谓“小得多”,一般情况弹簧质量小于小球质量10倍以上,则可以忽略弹簧质量,即视为轻质弹簧[1].那么关于牛顿第二定律瞬时性问题中的轻质弹簧,是否一样的条件呢?
如图3所示,弹簧两端受力分别是F1和F2.以弹簧作为研究对象,设弹簧质量m0,不考虑其他外力,由牛顿第二定律有
F1-F2=m0a
若m0a→0,即弹簧合外力始终为零,此时必有F1=F2.因此轻质弹簧可以认为是合外力始终为零的弹簧,当加速度a不太大,弹簧质量m0→0时,可认为是轻质弹簧.可以看出,轻质弹簧两端受力(由牛顿第三定律,两端受到的力等于弹簧两端弹力)一定大小相等.反之,若弹簧两端受力(弹力)明显不相等,则此时就不能把弹簧当做轻质弹簧处理,因为弹簧合力一定不为零.如图2所示情景中,剪断细线,考虑到弹簧恢复形变一定需要时间,可以认为弹簧下端受B的拉力不变,但是弹簧上端显然已经没有物体对弹簧施力,因此这里不能将弹簧视为轻质弹簧.

图3
2 问题的解释
2.1 弹簧弹力的本质
物质是由大量分子组成,弹性源于组成物质的分子间的相互作用力.在力学上我们只需要研究整体受力与形变的关系,而不必分析物质分子中每个分子的受力.弹簧受到外力时,考虑弹簧中一微小截元,如图4所示.假想平面S与弹簧弹力平行,弹簧弹力的主要贡献源就是图4中所示的切应力F[2].这个切应力的作用是使弹簧恢复形变.弹簧静止时,各部分切应力(弹力)相等.
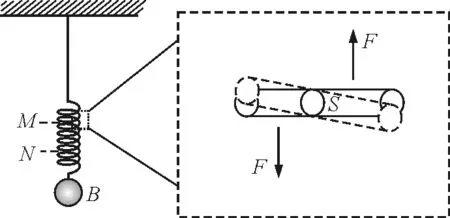
图4
2.2 对图2模型的解释
上文已明确指出,图2模型中剪断细线时弹簧不满足轻质弹簧的条件.考虑到弹簧恢复形变一定需要时间(尽管这个时间很短),剪断细线瞬间弹簧各部分弹力相等.从整体看,瞬间物体B受力不变,弹簧整体受到B对其竖直向下的拉力,这个拉力使弹簧质心产生竖直向下的加速度,效果是使弹簧恢复形变.

3 结论
(1)只有在弹簧两端同时受力,且弹簧合外力视为零时才有“轻质弹簧”一说.
(2)当弹簧只有一端受力时,不能把弹簧视为轻质弹簧,此时的各部分弹力的作用是使弹簧收缩,而且不同部分收缩的速度不同.
参考文献
1 肖立.怎样的弹簧才是“轻质弹簧”.物理教学探讨,2005(19)
2 潘武明.力学.北京:科学出版社,2004.183

