Ostrowski型不等式的伙伴的加权推广*
时统业,姜卫东,宋祥斌
(海军指挥学院浦口分院,江苏南京 211800)
Ostrowski型不等式的伙伴的加权推广*
时统业,姜卫东,宋祥斌
(海军指挥学院浦口分院,江苏南京 211800)
通过建立二阶可微函数的积分恒等式,对于具有绝对连续导函数的函数,给出了Ostrowski型不等式的伙伴的一个加权推广.
Ostrowski型不等式;二阶可微函数;梯形不等式;中点不等式

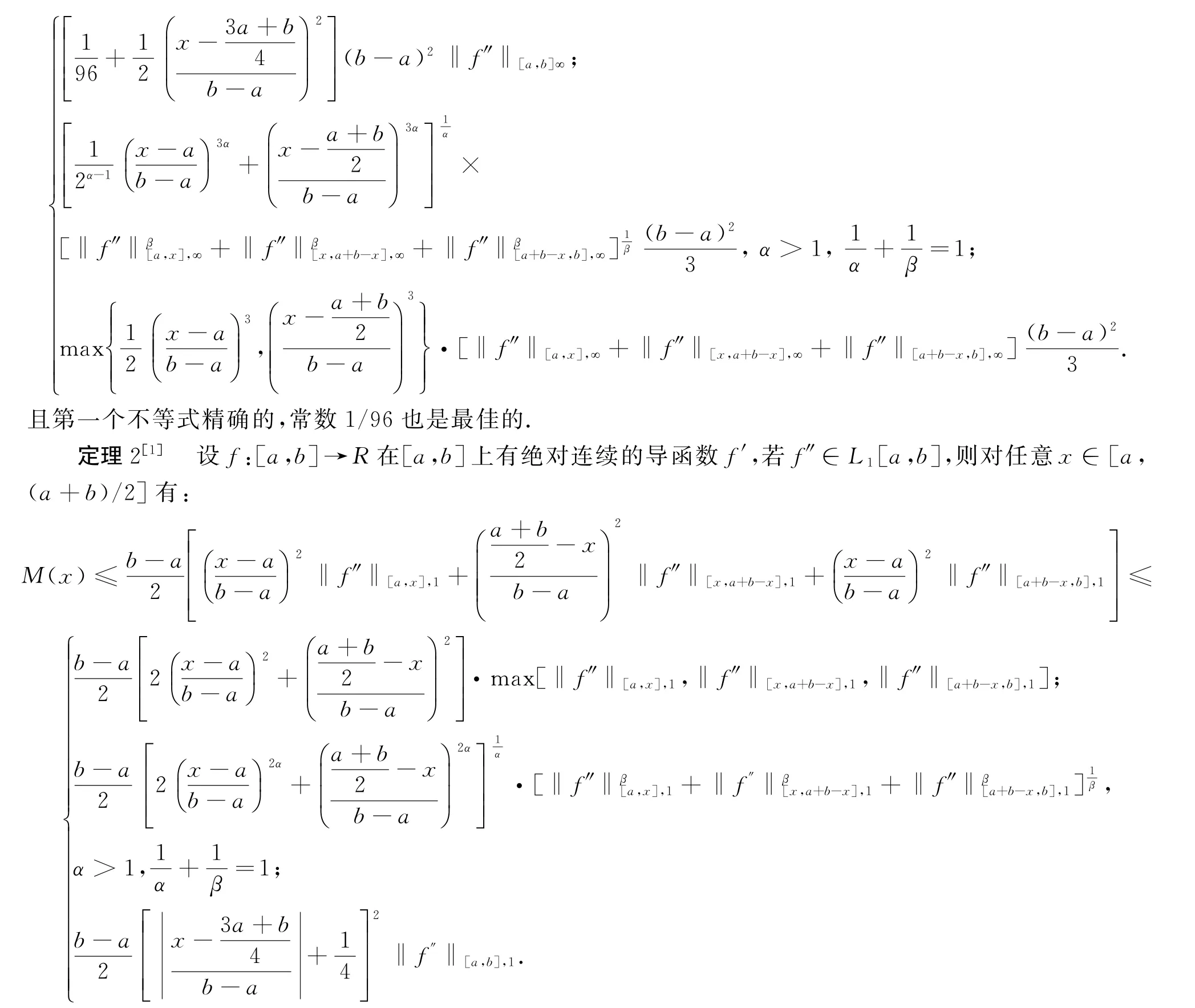
本文给出引理1的加权推广,并仿照文献[1]的方法,对Ostrowski型不等式的伙伴加权推广.先引入三个函数并给出其性质.
定义1设g:[a,b]→R是正的可积函数,且关于t=(a+b)/2对称,记:

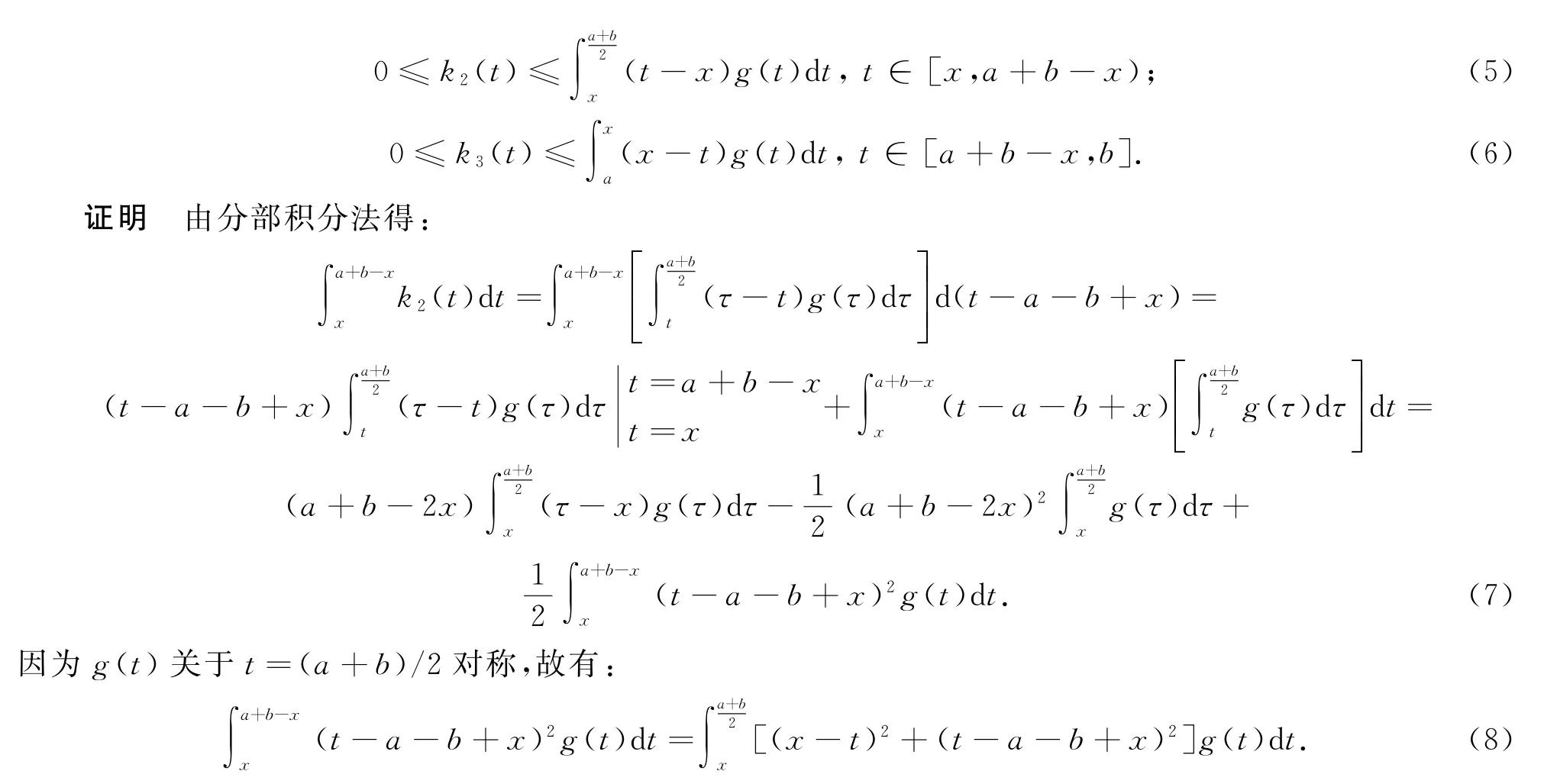
由式(7)、式(8)证得式(2).类似可证式(1)和式(3).

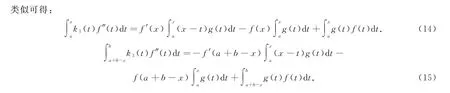
式(13)、式(14)、式(15)相加,得到式(9),引理3证毕.
注1在引理3中取g(t)≡1得到引理1.
1 主要结果



证明由引理2的式(4)、式(5)、式(6)易证第一个不等式和最后部分的第一个不等式.由Hölder不等式证得最后部分的第二个不等式.
最后部分的第三个不等式的证明:

[1]Liu Zheng.Some companions of an Ostrowski type inequality and applications[J].J Inequal Pure Appl Math,2009,10(2):52.
A Weighted Generalization of Some Companions of the Ostrowski-type Inequality
SHI Tongye,JIANG Weidong,SONG Xiangbin
(Institute of Pukou,Naval Commanding College,Nanjing 211800,China)
This paper derives a general integral identity for twice differentiable mappings,and establishes a weighted generalization of some companions of Ostrowski type inequality for functions whose derivatives are absolutely continuous.
Ostrowski-type inequality;twice differentiable mappings;trapezoid type inequality; midpoint inequality
O178
A
1009-1734(2014)02-0016-07 MSC(2000):26D15
0 引言
具有绝对连续导函数的函数建立了一些Ostrowski型不等式的伙伴. *
2013-10-20
收稿日期:2013-10-20
时统业,副教授,研究方向:基础数学教学和研究.E-mail:shtycity@sina.com
MSC 2000:26D15

