η-广义混合向量平衡问题解的存在性*
李紫嫣,高大鹏,何中全
(西华师范大学数学与信息学院,四川南充 637002)
η-广义混合向量平衡问题解的存在性*
李紫嫣,高大鹏,何中全
(西华师范大学数学与信息学院,四川南充 637002)
在Bana c h空间中,引进和研究了一类η-广义混合向量平衡问题(η-GMVEP),在适当假设条件下证明了此类问题的等价性定理,并运用KKM定理得到其解的存在性定理.
η广义混合向量平衡问题;伪单调;Hausdorff度量;KKM映射;存在性
0 引言
最近几年,向量变分不等式成为在自然科学和社会科学的很多研究领域的重要工具,并都得到了广泛的应用.向量变分不等式作为变分不等式的推广,最早是由Giannessi在1980年引入到有限维欧式空间中并加以研究的[1].随后,向量变分不等式、向量拟变分不等式和其补问题等在无限维空间中得到了广泛研究和推广[2~6].另一方面,向量平衡问题也得到了深入的研究[7~11].受文献[4]、[12]、[13]的启发,本文引入了一类新的η-广义混合向量平衡问题,并运用KKM定理,得到了此问题解的存在性定理.
1 预备知识

此问题在文献[6]、[16]中被引入和研究.

此问题在文献[18]中被引入和研究.
为了得到本文的结果,需要下面的定义和引理.
定义1[19]K是拓扑线性空间X中的非空子集.集值映射F∶K→2Y称作KKM映射,如果对任意的非空有限子集{u1,u2,…,un}⊆K,总有:

2 主要结果与证明
定理1设X,Y为实的Banach空间,K⊆X为非空凸子集,{C(u):u∈K}是Y中的真的闭凸锥,


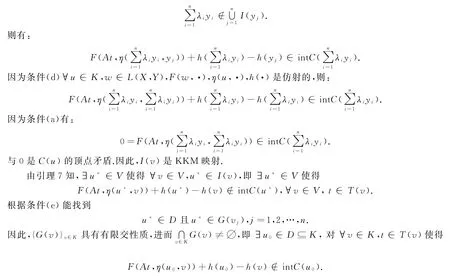
余下仿定理1证明即可.
[1]Giannessi F.Theorems of alternative,quadratic programs and complementarity problems[J].Variational inequalities and complementarity problems,1980(1):151-186.
[2]Chen G Y,Cheng G M.Vector variational inequality and vector optimization problem[M].Berlin:Springer Berlin Heidelberg,1987.
[3]Lee G M,Lee B S,Chang S.On vector quasivariational inequalities[J].Journal of Mathematical Analysis and Applications,1996,203(3):626-638.
[4]Ansari Q H,Farajzadeh A P,Schaible S.Existence of solutions of a vector variational inequalities and vector complementary problem[J].Journal of Global Optimization,2009,45(2):297-307.
[5]Lee G M,Kim D S,Lee B S,et al.Generalized vector variational inequality and fuzzy extension[J].Applied Mathematics Letters,1993,6(6):47-51.
[6]Siddiqi A H,Ansari Q H,Khaliq A.On vector variational inequalities[J].Journal of Optimization Theory and Applications,1995,84(1):171-180.
[7]Zeng L C,Yao J C.An existence result for generalized vector equilibrium problems without pseudomonotonicity[J].Applied Mathematics Letters,2006,19(12):1-320-1-326.
[8]Huang N J,Li J,Thompson H B.Implicit vector equilibrium problems with applications[J].Mathematical and Computer Modelling,2003,37(12):1-343-1-356.
[9]Konnov I V,Yao J C.Existence of solutions for generalized vector equilibrium problems[J].Journal of Mathematical A-nalysis and Applications,1999,233(1):328-335.
[10]Ansari Q H,Schaible S,Yao J C.System of vector equilibrium problems and its applications[J].Journal of Optimization Theory and Applications,2000,107(3):547-557.
[11]Zeng L C,Yao J C.Generalized Minty’s lemma for generalized vector equilibrium problems[J].Applied Mathematics Letters,2007,20(1):32-37.
[12]Preda V,Beldiman M,Bǎtǎtorescu A.On variational-like inequalities with generalized monotone mappings[M].Ber-lin:Springer Berlin Heidelberg,2006.
[13]Li X,Kim J K,Huang N J.Existence of Solutions forηGeneralized Vector Variational Like Inequalities[J].Journal of Inequalities and Applications,2010(1):1-13.
[14]Khan M F.On generalized vector variational-like inequalities[J].Nonlinear Analysis:Theory,Methods&Applications,2004,59(6):879-889.
[15]Lee B S,Lee G M.A vector version of Minty’s lemma and application[J].Applied Mathematics Letters,1999,12(5):43 -50.
[16]Jung D Y.Some generalization of Minty’s lemma[J].J Korea Soc Math Educ Ser B:Pure Appl.Math,1999,6(1):33-37.
[17]Khaliq A,Rashid M.On generalized vector quasivariational-like inequality problems[J].Fixed Point Theory and Applications,2005,2005(3):243-255.
[18]Chen G Y,Li S J.Existence of solutions for a generalized vector quasivariational inequality[J].Journal of Optimization Theory and Applications,1996,90(2):321-334.
[19]Knaster B,Kuratowski C,Mazurkiewicz S.Ein Beweis des Fixpunktsatzes für n-dimensionale Simplexe[J].Fundamenta Mathematicae,1929,14(1):132-137.
[20]Chen B,Huang N J.Vector variational like inequalities and vector optimization problems in Asplund spaces[J].Optimization Letters,2012,6(7):1-513-1-525.
[21]Fan K.A generalization of Tychonoff’s fixed point theorem[J].Mathematische Annalen,1961,142(3):305-310.
[22]Nadler Jr S B.Multi valued contraction mappings[J].Pacific J Math,1969,30(2):475-488.
Existence of Solutions forηGeneralized Mixed Vector Equilibrium Problems
LI Ziyan,GAO Dapeng,HE Zhongquan
(School of Mathematics and Information,China West Normal University,Nanchong 637002,China)
This paper introduces some generalized mixed vector equilibrium problems in Banach spaces and proves the equivalence of the two classes ofηgeneralized mixed vector equilibrium problems under suitable assumptions.By using the equivalence theorem,we obtain some results on the existence of solutions forηgeneralized mixed vector equilibrium problems.
ηgeneralized mixed vector equilibrium problems;pseudo monotone;Hausdorff metric;KKM-mapping;the existence
O177.92
A
1009-1734(2014)02-0006-06 MSC(2000):49J35,90C47
2013-12-10
教育部科学技术重点项目(211163);西华师范大学基金项目(11A029,11A028)、(13D016).
何中全,教授,研究方向:非线性分析.E-mail:sasaweb@sina.com
MSC 2000:49J35,90C47

