指示元素垂向分带序列计算方法述评

叶庆森

(核工业二三○研究所，长沙 410007)

0 前言

矿床原生晕指示元素垂向分带规律的研究有助于正确判断矿床(体)剥蚀程度，寻找隐伏矿床(体)，是构造地球化学原生叠加晕找矿和地球化学模式找矿的基础。元素地球化学活动性的差异使得不同指示元素的原生晕在空间上呈现序次分布(组分分带)。在二十世纪七十年代前苏联学者格里戈良提出指示元素垂向分带指数计算法[1]的基础上，国内化探界学者先后提出了多种计算方法，主要有广义衬值法、浓集重心法、浓集指数法、比重指数法、含量梯度法等[2-9]，为元素分带序列研究方法的不断发展和完善做出了贡献。下面就上述几种主要的计算方法予以简单介绍，并指出各自的特点。

1 分带指数法

分带指数法[1]是一种传统的原生晕指示元素分带序列计算方法，由前苏联学者格里戈良提出。它是根据指示元素分带指数的最大值所在截面(中段)位置由浅至深将指示元素顺序排列。

1.1 计算方法

以A矿床为例，其计算步骤可概括如下：

(1)计算各截面有关指示元素的线金属量(表1)，并按元素逐一标准化至同一数量级。

(2)计算不同截面各指示元素的分带指数值D(表2)。某指示元素的分带指数最大值(Dmax)所在的截面即为该指示元素在分带序列中的位置，由此就可初步排出它们之间自上而下的分带序列为：Au、Ag、Pb-W-Sn、Cu、Co-Bi。如果某截面同时存在两个或多个元素Dmax，则需进行下一步计算。

表1 A矿床8个指示元素在不同截面的线金属量(m·10-6)

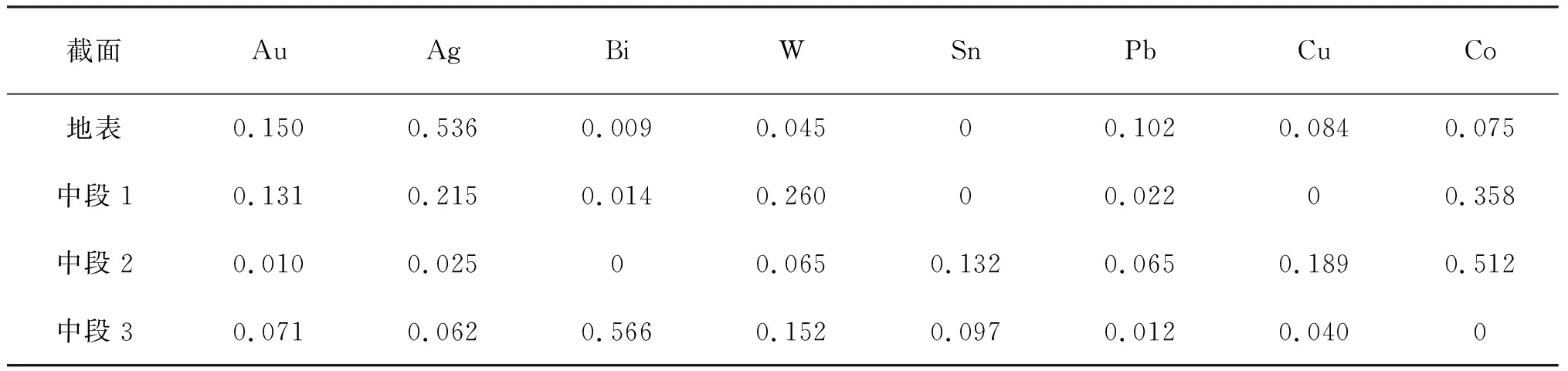
表2 A矿床8个指示元素的分带指数值

(3)计算指示元素的分带指数梯度值ΔG，比较ΔG的大小即可确定各元素在垂向分带序列中的确切位置。ΔG大者在上，小者在下，设共有p个截面参与计算。

(1)

式(1)中D1、Dm、Dp分别是当两个或多个指示元素的Dmax同在最上截面(如地表)、同在中部截面、同在最下截面时相应元素的Dmax值；Dl为某指示元素在l截面的分带指数值。

从公式(1)可以看出，当指示元素的异常不连续即某截面无异常时，就必须人为地赋给Dl一定的数值，否则线金属量Dl为“0”，就无法计算出ΔG的值。

如A矿床中Au、Ag、Pb和Sn、Cu、Co的Dmax分别同在最上截面(地表)和中部中段2，同时Sn、Cu、Co在某些截面出现了异常不连续(线金属量为“0”)的情况。为计算ΔG，将指示元素标准化线金属量为“0”的相应位置赋值0.001。计算结果表明，Au、Ag、Pb和Sn、Cu、Co自上而下的确切垂向分带序列分别为Ag-Au-Pb和Co-Cu-Sn。

因此本例确切的分带序列为：Ag-Au-Pb-W-Co-Cu-Sn-Bi。

需要指出，如果在表1中分别删去Bi和Sn，利用分带指数法分别重新计算剩余7个元素的分带指数(表3、表4)和必要的ΔG，可分别得出垂向分带序列Ag-Pb-Co-Cu -W-Au-Sn和Ag-Au-Pb-W-Co-Cu-Bi。

比较表2(8个元素)和表3(据表1中去掉Bi所在列计算)可以看出，两者的垂向分带序列发生了明显变化，即由于参与计算的指示元素的个数不同，分带序列发生了变更，如根据表2(8个元素)，Au排在第2位，但根据表3，Au却排到第6位。同样比较表3和表4(分别据表1中去掉Bi和Sn所在列计算)可见，两者的分带序列也有明显变化，如依照表3，Au排到第6位，但依照表4，Au却排在第2位了。

1.2 特点

纵观上述计算过程可知，格里戈良分带指数计算法虽然面世最早，也曾一度视为“经典”，但其不足之处是显而易见的，如：

(1)该方法的计算过程比较复杂。

(2)当某指示元素在某中段异常不连续，线金属量为“0”时，必须人为地赋给一个很小的非“0”值，否则垂向分带序列无法计算。然而这个很小的非“0”值可能对整个计算结果产生较大的影响，这显然是不客观的。

表3 A矿床Au、Ag、W、Sn、Pb、Cu、Co的分带指数值

表4 A矿床Au、Ag、W、Pb、Cu、Co、Bi的分带指数值

(3)由于某指示元素的分带指数值可随参与计算的元素多寡、种类及其他元素线金属量而变，从而影响其在分带序列中的位置。由于各种条件的限制和影响，在实际工作中参与计算的指示元素种类和数量不可能且没有必要完全统一。由此可见，由于参与计算的指示元素种类和数量的人为抉择会使客观存在的分带规律发生改变。

综上所述，该计算方法确实问题不少。

2 广义衬值法

顾名思义，广义衬值法[2]是从衬值或衬度(异常含量Ca与背景值Cb之比)的概念扩展而来。

2.1 计算方法

广义衬值法的计算步骤如下：

(1)求指示元素在各截面的广义衬值Km：

(2)

式(2)中Nm为m截面的样品总数；Ci为指示元素在m截面样品i的含量；Li为m截面样品i的有效控制长度；Cb为指示元素的地球化学背景值。广义衬值Km的意义相当于格里戈良法中分带指数D。

(2)找出各指示元素广义衬值最大值(Kmax)所在的截面位置，据此初步排出它们的垂向分带序列。

(3)当某截面有两个或多个指示元素的广义衬值K同时为最大值时，则需按式(3)求广义衬值梯度ΔGk(设有p个截面)。根据ΔGk的大小，可确定指示元素在垂向上的分带序列，大者为上，小者为下。某指示元素的ΔGK定义如下：

(3)

式(3)中K1、Km、Kp分别是当两个或多个指示元素的Kmax同在最上截面(如地表)、同在中部截面、同在最下截面时相应元素的Kmax值；Kl为某指示元素在l截面的广义衬值。

根据该计算方法，可得到上述A矿床不同截面8个指示元素的广义衬值(表5)和自上而下的垂向分带序列(Ag-Au-Pb-W-Co-Cu-Sn-Bi)；即使表5中分别去掉Bi和Sn所在列后分别计算，得到的分带序列为Ag-Au-Pb-W-Co-Cu-Sn和Ag-Au-Pb-W-Co-Cu-Bi，仍没发生序次变化。

2.2 特点

(1)克服了格里戈良分带指数计算法中当指示元素的异常在某截面不连续时，分带指数梯度值ΔG无法直接计算的弊端。

(2)在广义衬值法中，指示元素广义衬值的计算是相互独立的，因此广义衬值不受其它元素的影响，即不会因参与计算的指示元素不同或多寡而使其在分带序列中的位置发生变化。

(3)广义衬值具有传统衬值(即衬度)的概念，因而可揭示各指示元素在各截面的富集程度，从而能更客观地反映指示元素分带现象，地球化学意义明确。

(4)该方法数学意义非常明确，计算过程比格里戈良分带指数法简单得多，比如在广义衬值法中，数据不需要标准化。

3 浓集重心法

该方法基于物理学原理。用刚性轻杆连结的n个质点的质心公式为

(4)

式(4)中mi为第i质点的质量；xi为第i质点在x轴上的坐标。

一般情况下，刚体的质心和重心相重合。如果把i截面的异常看成一个用轻杆连结的质点i，把指示元素的线金属量(Mi)看成i点的质量(mi)，把标高(hi)看成i点的坐标(xi)，那么就可以求出该元素的浓集重心的空间位置，从而能够定量研究元素的浓集重心在空间上的有序排列。

3.1 计算方法(设共有p个截面)

(1)计算各截面各指示元素的线金属量(M)(也可以用异常含量和来代替)。

(2)参照上述质心公式，求出各指示元素的浓集重心(H)，根据H的大小排出由上而下的垂向分带序列，大者在上，小者在下：

(5)

式中Ml为指示元素在l截面的线金属量；hl为l截面异常标高。

3.2 特点

(1)在部分截面无异常的情况下，仍可计算分带序列。

(2)计算出来的结果代表元素的浓集重心在空间上的分布位置，其数学意义和地球化学意义较明确。

(3)计算过程较简便，且其间各指示元素相互独立计算，即指示元素的浓集重心值不受其它元素的影响，因此不会因参与计算的指示元素不同或多寡改变元素在垂向分带序列中的位置。

4 浓集指数法

4.1 计算方法

(1)计算各指示元素在所有截面上含量之和的平均值CM：

表5 A矿床8个指示元素的广义衬值

(6)

式中Cl是指示元素在l截面的含量，假设共有p个截面。

(2)计算各截面各指示元素含量与相应元素的CM之比值，并把该比值定义为该截面该指示元素含量的标准化值。

(3)计算同一截面所有指示元素含量标准化值之平均值CMB。

(4)计算某截面不同指示元素的浓集指数CI。某截面某指示元素的浓集指数CI等于该截面该元素含量标准化值与该截面CMB之比，并按该指示元素的浓集指数最大值CImax所在截面位置初步确定分带序列。因为该比值越大，表明相应截面相应指示元素的浓集程度越高，故将该比值称为浓集指数。

(5)当某截面有两个或多个指示元素的浓集指数CI同时为最大值时，则按式(7)求浓集指数梯度ΔGCI(设有p个截面)。根据ΔGCI的大小，可确定出元素在垂向上的分带序列，大者为上，小者为下。某指示元素的ΔGCI定义为式(7)：

(7)

式(7)中CI1、CIm、CIp分别是当两个或多个指示元素的CImax同在最上截面(如地表)、同在中部截面、同在最下截面时相应元素的CImax值；CIl为某指示元素在l截面的浓集指数。

4.2 特点

(1)浓集指数方法与广义衬值法有类似之处，克服了格里戈良分带指数计算法中当指示元素的异常在某截面不连续时，分带指数梯度值ΔG无法直接计算的弊端。

(2)原始数据标准化的结果是唯一的，为无量纲化处理，能消除地壳中各元素丰度差可能给计算带来的影响。

(3)尽管各指示元素浓集指数的计算不相互独立，浓集指数值可因参与计算的元素多寡或种类而变，但初步验算表明，参与计算的指示元素多寡或种类不同不会影响指示元素在分带序列中的位置。

(4)该方法的计算过程较复杂。

5 比重指数法

5.1 计算方法

(2)求指示元素i在l截面的比重指数Hli(即某指示元素在某截面的线金属量占该指示元素在所有截面线金属量总和之比例)：

(8)

式(8)中Mli为指示元素i在l截面的线金属量，设共有m个截面(l=1，2，…，m)。

某指示元素i在某截面的比重指数Hi值大，则该元素在该截面所占的比重大。某指示元素i的比重指数最大值Himax所在的截面位置(自上而下)就是该元素在垂向分带中的位置。

(3)当两个或多个指示元素的Himax同在某截面时，可通过直接比较Himax的大小，来确定它们的具体位置：

当Himax同在最下截面时，大者为下。

当Himax同在某中部截面时，则相应指示元素i在该截面及其以上截面的Hi值之和∑M上大者或以下截面的Hi值之和∑M下小者为上。

5.2 特点

比重指数方法与广义衬值法有类似之处：

(1)无需标准化计算，计算过程比较简单。

(2)比重指数Hi值是通过同元素同量纲的关系来计算所占比重的，即指示元素Hi值的计算是相互独立的，不会因参与计算的指示元素不同或多寡而使元素在分带序列中的位置发生变化。

(3)该方法只需计算元素比重指数Hi，不必计算分带指数梯度值ΔG，因而克服了当指示元素异常在某截面不连续时，ΔG无法直接计算的弊端。

6 含量梯度法

含量梯度法通过直接比较同一指示元素在各截面的含量大小来确定指示元素的垂向分带序列。它与概率梯度法[10]基本相同，但比后者更简便。

6.1 计算方法

(1)列出参与计算的所有指示元素在各截面中的含量。

挑取1～2环接入细菌斜面培养基上，37℃培养24 h后，用无菌生理盐水洗下菌苔，制成菌悬液。采用麦氏比浊法，用无菌生理盐水调节细菌含量为1×108cfu/ml。

(2)逐一比较同一指示元素在各截面中的含量，含量最大值Cmax所在的截面位置即为该元素在垂向分带中的位置，据此得出基本的分带序列。

(3)当两个或多个指示元素的Cmax同在某截面时，则需比较含量梯度ΔGC的大小来确定指示元素在分带序列中的确切位置。ΔGC大者为上，小者为下。

某指示元素的ΔGC定义为式(9)：

(9)

式中C1、Cm、Cp分别是当两个或多个指示元素的Cmax同在最上截面(如地表)、同在中部截面、同在最下截面时相应元素的Cmax值；Cl为某指示元素在l截面中的含量。

6.2 特点

(1)含量梯度法与广义衬值法、比重指数法等有类似之处，均通过同元素同量纲的关系来计算所占比重，即各指示元素含量梯度值的计算相互独立，因而不会因参与计算的指示元素不同或多寡而使指示元素在分带序列中的位置发生变化。

(2)该方法数据不需要标准化，计算过程更简便。

(3)当指示元素的异常在某截面不连续时，不会造成分带序列无法直接计算的现象。

(4)不足之处是该方法只考虑指示元素在各截面、各采样点的含量，忽略了各采样点指示元素含量的有效控制长度，即忽略了其含量的权重。因此为客观全面起见，在确定各截面指示元素含量时，必须考虑各采样点的有效控制长度。

7 结语

上述六种确定矿床原生晕指示元素垂向分带序列的计算方法是近年来地质文献中应用频率较高的方法。作者认为：

(1)虽然广义衬值法、浓集重心法、浓集指数法、比重指数法、含量梯度法一般都能克服格里戈良分带指数计算法中当指示元素的异常在某截面不连续时，分带指数梯度值ΔG无法直接计算的弊端，但由于浓集指数法中各指示元素浓集指数值的计算并非相互独立，即同一矿床原生晕指示元素的浓集指数值可因参与计算的元素多寡或种类而变，而且其计算过程较复杂；含量梯度法仅考虑指示元素在各截面的含量，忽略了各采样点指示元素含量的有效控制长度，因而该方法尚需完善和改进。由此可见，广义衬值法、浓集重心法和比重指数法相对合理和客观，其计算方法比较简单，值得推广。

(2)格里戈良分带指数法虽然比较经典，但由于异常不连续，即某截面无异常时，其分带指数梯度值ΔG无法直接计算而影响排序；而且某指示元素在分带序列中的位置会因参与计算的指示元素不同或多寡而改变，因此不值得推广。

(3)值得指出的是文献[7]未正确介绍格里戈良分带指数法(该方法并非将“各元素的含量换算成同一数量级次”)；文献[8]介绍的数据标准化，未考虑到不同指示元素的含量级差大(如Au和Cu)时，无法实现标准化到同一数量级的情况。

(4)在计算矿床原生晕指示元素分带序列前，必须查明控矿因素、综合分析成矿地质条件、分解成矿作用期次及各期次指示元素组合，以便建立单一成矿期次的指示元素垂向分带理想模型，合理解释由于构造叠加晕引起的元素分带序列“反常及反分带现象”[11]。这对指导化探异常评价、提升矿产预测水平、提高模型找矿的效果意义重大。

参考文献：

[1] 地质矿产部情报研究所．勘查地球化学手册：第二卷[M]．北京：冶金工业出版杜，1990．

[2] 叶庆森，冯倡，滕润球. MS岩体中段铀矿床地球化学异常模式及其找矿意义[J]. 铀矿地质，1988,4(6)：340-347.

[3] 朴寿成，连长云. 一种确定原生晕分带序列的新方法——重心法[J]. 地质与勘探，1994,30(1)：63-65.

[4] 解庆林. 浓集指数法确定矿床原生晕元素轴向分带序列[J]. 地质与勘探，1992,33(6)：55.

[5] 赵琦. 原生晕垂直分带的元素比重指数计算法[J]. 物探与化探. 1989,13(2)：157-159.

[6] 张定源. 银岩锡矿原生晕元素分带序列计算方法研究[J]. 地质与勘探，1989,25(6)：45-49.

[7] 王建新，臧兴运，郭秀峰，等. 格里戈良分带指数法的改良[J]. 吉林大学学报：地球科学版， 2007,37(5)：884-888.

[8] 邢利琦，刘炳璋. 矿床原生地球化学晕分带性研究[J]. 四川地质学报，2011,31(4)：489-495.

[9] 金献革. 矿床原生晕元素空问分带序列计算方法研究[J]. 科技与企业，2012(20): 274-275.

[10] 邱德同. 确定矿床原生晕指示元素分带序列的新方法[J]. 地质与勘探，1989,30(8)：51-53.

[11] 李惠，禹斌，李德亮，等. 构造叠加晕找盲矿法及研究方法[J]. 地质与勘探，2013,49(1): 154-161.