提高干涉条纹清晰度的条件

李春燕 周 梅 何志巍 金仲辉

(中国农业大学理学院 北京 100083)

满足相干三条件的两束光[1～3]，在它们相遇区域可形成干涉条纹，但干涉条纹是否清晰还和其他的因素有关．我们知道，两束光相干涉后的光强I(P)为

(1)

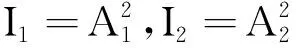
当δ= 2kπ时，k= 0，±1，±2，…，干涉光强达到最大值

(2)

当δ=(2k+1)π时，k= 0，±1，±2，… ，干涉光强达到最小值

(3)

干涉条纹清晰度和干涉区内光强度的起伏情况有关．起伏大，说明干涉条纹清晰；反之，不清晰．为了对干涉区域内光强度起伏程度做出定量的描述，为此定义干涉条纹的衬比度

(4)

其中IM和Im分别代表干涉光强的最大值和最小值．当Im= 0时，有γ=1，干涉条纹最清晰．将式(2)、式(3)代入式(4)有

(5)

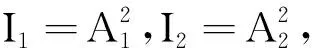
(6)

若A1=A2，则γ=1；若A1= 3A2，则γ=0.6；若A1= 10A2，则γ=0.2．

由此可得出结论，相干的两束光的振幅越接近，γ值越大．γ的最大值为1，条纹最清晰；γ的最小值为零，说明相干区域光强均匀分布无起伏，不出现干涉条纹，对应为完全非相干叠加．

在以上讨论了两相干光束的振幅对干涉条纹的衬比度影响后，现在来讨论光强均为I0的两束相干自然光束的传播方向有一夹角α情况下的干涉条纹衬比度．

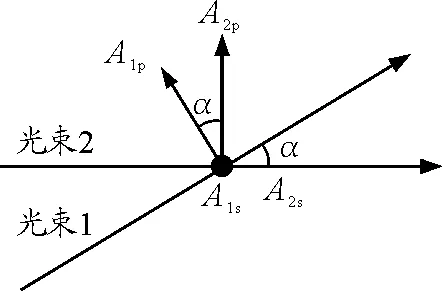
图1

(7)

(8)

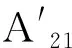
(9)

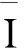
(10)

(11)

于是有

(12)

若α=10°，有γ=0.99；若α=30°，有γ=0.93；若α= 90°，有γ=0.50．由此可见，在两束自然光传播方向夹角较小情况下，干涉条纹依然是很清晰的．

总之，由本文讨论过程可看出，为了得到清晰的干涉条纹，除了满足相干三条件外，还需满足下列的两个条件：

(1)相干叠加的两束光的振幅尽可能接近；

(2)相干叠加的两束光的传播方向间的夹角不要太大．

参考文献

1 吴百诗.大学物理学(下册).北京：高等教育出版社，2004.189～190

2 马文蔚，周雨青，解希顺. 物理学教程(下册). 北京：高等教育出版社，2006.180～182

3 金仲辉，柴丽娜.大学基础物理学. 北京：科学出版社，2010.261～262