基于线性规划的某特大桥施工扣索索力优选分析

张耀庭， 颜燕祥， 张正哲， 李艳芳， 张 敏

(1.华中科技大学 土木工程与力学学院，湖北 武汉 430074；2.湖北工程学院 城建学院，湖北 孝感 432000；3.辽宁省水利水电科学研究院，辽宁 沈阳 110003;4.武汉市蔡甸区公路管理局，湖北 武汉 430100；5.湖北省交通规划设计院，湖北 武汉 430051)

对斜拉桥、连续刚构桥等大跨度桥梁结构工程而言，钢索(如斜拉索、施工临时扣索等)索力的大小直接影响到桥梁结构的内力和线型[1～4]。在工程界，设计者大多仅凭主观经验从设计验算的角度来设计钢索拉力。为了有效地控制桥梁设计线型状态，必须在施工阶段进行索力调整，索力调整一直以来也是依靠经验反复进行的。因此，理论界和工程界一直在探寻求解最优索力的方法，以便通过尽量少次数的索力调整，甚至不进行索力调整，快捷地得到安全状态和使用状态下的合理索力。索力优选在斜拉桥方面的研究成果斐然[4～6]，描述索力与桥梁状态的关系及处理方法有：前进分析法、倒退分析法、状态比较法、正装迭代法、前进-倒退迭代法、无应力状态分析法等。然而，针对其它桥型的钢索索力优化研究则相对较少，对施工中的拉索索力进行优化设计的工程实例就更少。钢索索力的优化不仅可以实现工程结构的安全，达到节约钢材、降低造价的目的，还可以减少施工过程中的调索次数，缩短张拉过程及时间。基于上述目的，在大跨径预应力桥梁和拱桥的无支架施工，以及斜拉桥、悬索桥等索桥的索力优选等方面，寻求概念明晰、操作简单、结果可靠的索力优选的分析方法，已成为工程界的必需。本文以某大型空腹刚构桥为工程背景，在通用有限元程序ANSYS中，采用beam189单元模拟空腹刚构桥的三角区的下弦钢筋混凝土曲梁，用link8单元模拟其下弦杆施工过程中的体外施工(临时)扣索，运用线性规划原理，以应力和变形作为理论约束条件、以索力均匀作为人为约束条件，在严格控制施工标高的前提下，以节约钢束用量为目标；借助MATLAB实现了结构在线性工作阶段的索力优选，得到了临时扣索在施工过程中的最优索力，从而更好地保证该桥下弦在施工时的质量、进度与安全。

1 工程背景

北盘江特大桥位于贵州省六盘水市水城县发耳镇和营盘乡交界处，全桥长1261 m，为一种新型的空腹式刚构桥。桥跨布置为(5×30 m)+(82.5 m+220 m+290 m+220 m+82.5 m)+(3×30 m)+(4×30 m)。其中主桥为82.5 m+220 m+290 m+220 m+82.5 m，为预应力混凝土空腹连续刚构桥。

该空腹刚构桥施工时，主悬浇“T”梁为空腹式 “T”构，其斜腿三角区分上、下弦设置，上下弦各自浇筑11个节段后在第12个节段处交汇，空腹区合拢前为上下弦分离区段，11个节段共计浇筑长度为44 m，单个节段长度为4.0 m；从第12节段到第34节段，为上、下弦合并区段，最大节段长度为4.5 m；0号块施工完成后，在0号块上拼装上弦挂篮，用上弦挂篮浇筑上弦第一个节段后，张拉上弦第一个节段的临时体外索，下放挂篮的底篮部分至下弦下缘，用上弦挂篮浇筑下弦的第一个节段并张拉扣索，将上弦挂篮前移到上弦的第一个节段前端，浇筑下弦第二个节段并张拉扣索；拼装下弦挂篮，并完成上弦挂篮的底篮和下弦挂篮主桁的交接，形成最终的下弦挂篮，用下弦挂篮浇筑三角区的下弦斜腿3～11号节段，见图1(图1中对应下弦杆节段块的名称为ZX3-ZX11，下同)，并逐段张拉扣索，并在已浇筑完成的下弦斜腿的顶面用钢管搭设满堂支架，浇筑上弦的2～11号节段。

因此，该桥下弦扣索的合理张拉力的确定，对空腹区合拢前的施工安全和设计线型尤为关键。上弦11号节段施工完成后，重新完成下弦挂篮的底篮和上弦挂篮主桁架的交接，用合并后的挂篮浇筑余下的12～34号节段。

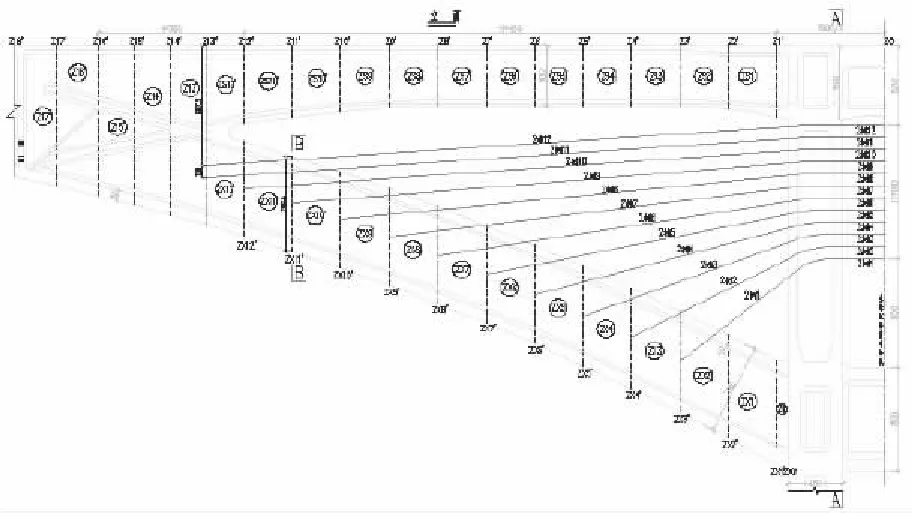
图1 某空腹刚构桥半边空腹区及施工(临时)扣索

2 扣索索力施工过程中的优选确定

2.1 线性规划原理与工程应用结合简介

线性规划[4～9]为运筹学的一个分支，是管理、科学、工程领域广泛应用的数学模型。它研究的内容是在一组线性等式(或不等式)组成的约束条件下，某个线性函数的最值问题，也称之为优化问题。它的研究内容可归纳为两个方面：一是系统的任务已定，如何合理筹划，精细安排，用最少的资源去实现这个任务，即求极小值问题；二是资源的数量已定，如何合理调配、利用，最好地完成任务，即求极大值问题。利用线性规划原理建立数学模型的三个步骤为：(1) 明确问题，列出约束条件；(2)建立模型；(3)求解模型(最优解)，进行优化后分析。

线性规划模型的基本结构为：(1)变量：变量又名未知数，它是实际系统的未知因素，也是决策系统中的可控因素，一般称为决策变量(本算例中变量为空腹区临时扣索索力)，常引用英文字母加下标来表示，如X1，X2，…,Xn等。线性规划的变量应为正值，因为实际问题中的变量所代表的均为实物，因此不能为负；(2)目标函数：将实际系统的目标，用数学形式表达出来，就称为目标函数，即系统目标的极值(本算例中为空腹区临时扣索索力之和最小)；(3)约束条件：约束条件是指实现系统目标的限制因素(本算例中为空腹区下弦杆箱梁根部与墩固结处的应力和下弦杆悬臂端点的挠度)，约束条件的数学表示形式为三种，即“≥”、“=”、“≤”。

2.2 施工索索力优选分析的原则与确定方法

现阶段国内外结构设计的方法[10]是近似概率的极限状态设计法。在实际设计和施工中，将关键截面的应力水平和关键点的变形控制在允许的范围内作为具体工程结构总体上的安全。对于加筋混凝土结构，我们控制关键截面最大拉应力和最大压应力，关键位置的最大挠度在允许的范围内，即S≤[S]；S代表着外荷载效应；[S]代表着结构或是实际生活经验的允许值。基于线性规划[11]的原理，线性规划的约束条件即本文中施工扣索索力优选的约束条件建立正是基于这种思路。本文采用控制特定点(下弦根部箱梁顶、底板)处的应力和悬臂端处的变形来建立结构索力的优化约束条件。也即：

(1)

以上三式分别表示了施工或运营过程中变形、拉应力强度和压应力强度的控制条件。

由于本次研究中，实际结构的变形和内力由外荷载和索力产生，即σ=σG+σQ+σGi，其三项分别为：σG恒载引起的截面某点的应力水平；σQ活载引起的截面某点的应力水平；σGi为张拉索在截面某点引起的应力水平。Δ=ΔG+ΔQ+ΔGi，其三项分别为：ΔG恒载引起的某点的变形；ΔQ活载引起的某点的变形；ΔGi为张拉索引起的某点的变形。只要合理控制扣索张拉力就可以实现现阶段结构线性工作阶段的设计性能目标和水准，达到索力优化设计的目的。考虑的施工荷载包括恒载、活载和张拉索力，在结构满足线性工作的条件下，结构响应可采用叠加法计算，本算例中关键截面位置的应力水平和挠度表达式如下：

(2)

(3)

式中：Xi为第i根索的索力，即在索长度和材料性质一定的条件下，索力最小，钢索的理论用量就最小。因此，本文中线性规划的目标函数为钢索用量的最小值。

2.3 工程实例计算与分析

依据上文所述，要利用线性规划原理实现施工扣索索力优选，就必须确定决策变量，以及由式(1)和式(2)确定的约束条件，还有式(3)确定的目标函数。本文采用ANSYS软件[11]进行北盘江特大桥结构的数值模拟，下弦曲杆箱梁采用beam189单元模拟，施工(临时)扣索采用link8单元模拟。采取简化的方法，将上弦杆的质量和支架荷载采用均布荷载的形式直接加在下弦杆箱梁上，不单独建立单元模拟满堂支架来表示下弦杆对上弦杆的支撑作用。相应的有限元模型如图2，分析计算时，考虑以下三种工况：

图2 ANSYS中的空腹区下弦杆及临时扣索有限元模型

工况1：上、下弦杆自重荷载；

工况2：挂篮包括对应块混凝土湿重400 t；

工况3：临时扣索拉力(每根索初拉力为100 kN)。

表1给出了有限元软件ANSYS计算的下弦相应块悬臂施工时，方程(2)中各系数在三种荷载工况下的有限元计算结果(下弦杆箱梁与墩交接处根部截面应力水平和悬臂端部的最大位移在对应工况下的影响系数)。恒载和挂篮产生的拉应力危险位置为下弦杆墩梁固结处下弦杆箱梁顶板，其压应力的危险位置为下弦杆墩梁固结处下弦杆箱梁底板；拉索产生的拉应力危险位置为下弦杆墩梁固结处下弦杆箱梁底板，压应力的危险位置为下弦杆墩梁固结处下弦杆箱梁顶板。恒载和挂篮产生的变形相对设计线型标高位置向下为正，扣索产生的变形相对设计线型标高位置向上为负。鉴于本结构的刚度较大，建模加载过程中每根钢索的初拉力以100 kN为相当的单位力，以免引起变形和应力变化较小，施工扣索拉力是通过初应变方法加上去的。

表1 方程(2)中各系数在三种荷载工况下的有限元计算结果

综上所述，本次优化以空腹区下弦根部箱梁顶、底板的应力和下弦悬臂施工端点的挠度为约束条件。空腹区自重和挂篮及节段湿重都使得下弦箱梁根部顶板受拉，底板受压，悬臂端点挠度向下；而拉索使得下弦箱梁根部顶板受压，底板受拉，悬臂端点挠度向上。由式(1)和(2)即可得到本工程的优化约束条件的实用表达式，各组表达式的物理意义分别为张拉第1根至第10根扣索时，空腹区下弦杆根部与墩固结处的顶板应力、底板应力、悬臂端挠度等的约束表达式，如式(4)、(5)、(6)即代表张拉第一根扣索时，空腹区下弦杆根部与墩固结处的顶板应力、底板应力、悬臂端挠度等应满足的约束条件。其它公式物理意义同前。

-2.65×107≤5.4351×107+0.56056×107-0.337610×106×(x1+x2+x3+x4+x5+x6+x7+x8+x9+x10)≤1.96×106

(4)

-2.65×107≤-5.9103×107-0.607992×107+0.293987×106×(x1+x2+x3+x4+x5+x6+x7+x8+x9+x10)≤1.96×106

(5)

-10×10-3≤0.3595185+0.049467264-0.002315×(x1+x2+x3+x4+x5+x6+x7+x8+x9+x10)≤10×10-3

(6)

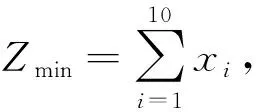
X={x1,x2,x3,x4,x5,x6,x7,x8,x9,x10}T

={24.8767,29.149,32.5294,29.6763,25.1841,

27.7959,27.7957,27.7957,27.7956,32.4283}T

(7)

表2设计索力和优化索力对比结果

扣索1扣索2扣索3扣索4扣索5扣索6扣索7扣索8扣索9扣索10总索力索力/kN设计值200020002750275027503000300032503250325028000优化解2487.672914.93252.942967.632518.412779.592779.572779.572779.563242.828502.7误差/%24.3845.7518.297.91-8.42-7.35-7.35-14.47-14.47-0.221.80

由表2可以看出：单根扣索索力的优化值相对设计院提供的索力值的最大偏差为+45.75%，最小偏差为-0.22%，总索力偏差+1.80 %(“+”表示优化值比设计值大，“-”则表示比设计值小)。产生上述偏差的主要原因为：在索力优化中考虑了拉索施工的先后顺序，在不同位置处的索，对关键截面的某点内力和控制点的挠度的影响程度不同，更主要的原因是在本工程实例中按线性规划原理优化计算扣索索力时，对挠度变形的控制更为严格。从总索力的对比结果可以看出，使用线性规划原理，在约束(应力和变形)条件下进行的索力优选具有可行性。

3 结 语

本文在北盘江大桥工程的施工(临时)扣索索力的确定中，在模拟施工顺序的同时，确保结构处于线性阶段的工作状态下，引入以扣索用量最少为目标函数，以拉索索力大小为控制变量，以关键截面应力和悬臂端点挠度为约束条件的线性规划的优化方法，对其施工过程中的临时扣索的设计索力进行了优选分析。计算结果和该桥现场施工均表明：将线性规划原理用于索力优化的方法，原理简单，操作方便易行，可以减少设计和施工过程中的调索次数，提高了扣索索力的计算精度。本文所提出的索力计算方法，为使用扣索或拉索结构的类似工程中索力的确定，提供了一种新的思路和方法。

[1] 胡云程, 王斌耀, 韦 林, 等. 结构预张力最大安全度设计[J]. 计算力学及其应用, 1984, 1(2): 23-29.

[2] 王永安, 刘世同, 谭红梅, 等. 斜拉桥索力优化理论研究[J]. 公路, 2006, (5): 31-34.

[3] 梁 鹏, 肖汝诚, 张雪松. 斜拉桥索力优化实用方法[J]. 同济大学学报(自然科学版), 2003, 31(11): 1270-1274.

[4] 何雄君，朱云升，邓旅成.连续梁桥基于预应力度配束方案的模糊优化决策[J]. 武汉交通科技大学学报，2000，24(l): 68-70.

[5] 钱令希. 工程优化设计[M]. 北京： 水利水电出版社, 1983.

[6] Utrilla M A, Samartin A. Optimized design of the prestress in continuous bridge decks[J]. Computers and Structures, 1997, 64(1-4): 719-728.

[7] Miehell A G M. The Iimits of economy of materials in frame struetures[J]. Philosophical Magazine Series 6，1904, 8(47): 589-597.

[8] Zhang W H, Domaszewski M, Bassir H. Developments of sizing sensitivity analysis with ABAQUS code [J]. Structural Optimization, 1999, 17 (2-3): 219- 225.

[9] Xie Y M，Steven G P. A simple evolutionary procedure for structural optimization[J].Computers and Structures, 1993, 49(5): 885-896.

[10] 叶见曙. 结构设计原理(第二版)[M]. 北京: 人民交通出版社，2005.

[11] 王新敏. ANSYS工程结构数值分析[M]. 北京: 人民交通出版社, 2007.

[12] K I 马吉德. 结构最优设计[M]. 北京: 中国建筑工业出版社，1980.

[13] JTG D62-2012，公路钢筋混凝土及预应力混凝土桥涵设计规范[S].

[14] JTG/T F50-2011，公路桥涵施工技术规范[S].