利用改进的分段VTEC多项式模型建立全天电离层变化模型

刘迪 ，段德磊，徐春

(云南省电力设计院，云南 昆明 650011)

1 引 言

电离层延迟误差是GPS 定位中的一项重要误差源，也是导致差分GPS 的定位精度随用户和基准站间距离增加而迅速降低的主要原因之一。目前现有的电离层模型主要是长时期内全球平均状况的经验模型［1］，如Bent 模型、Klobuchar 模型、IRI 模型等。利用这些模型来估计某一时刻某一地点电离层延迟的精度均不够理想，其误差为实际延迟量的20% ～40%［2］。近年来基于电离层单层假设的二维电离层模型的研究已趋于成熟，即利用地基GPS 实际测定某一时段某一区域内的电离层延迟，再采用数学方法拟合电离层延迟模型。显然，建立这种模型时并不要求对电离层变化规律有透彻的了解，一些时间尺度较长的不规则变化已经在模型中得到了反映［3］。本文利用VTEC 多项式模型对全天电离层TEC 进行了计算，但是采用此方法所得VTEC 值在分段模型间不连续。为此，本文通过增加已知条件和模型间取加权平均值的方法，能够很好地反映电离层电子总含量的实际情况，能较好保证模型间的连续性，并且带限制条件模型有利于提高长时间的电离层延迟模型的精度。

2 VTEC 多项式模型

VTEC 多项式模型是目前使用最多的局部电离层函数模型。该模型将VTEC 看做是纬度差φ－φ0和太阳时角差S－S0的函数，用一个规则的曲面来拟合各穿刺点处实际测定VTEC 值，其具体表达式为［4］:

式中:nmax、mmax是地理纬度φ 和日心经度S 二维多项式的泰勒展开式中的最大维数;Enm是VTEC 多项式模型的系数;φ0是测区中心点的地理纬度;S0是测区中心点在该时段中央时刻t0时的日心经度;φ 是穿刺点或者星下点的地理纬度。S 是穿刺点或者星下点的日心经度，它与地方时(LT)有关。

根据GPS 与VTEC 的关系，测站至卫星路径上的总电子含量的观测方程如下:

在本文计算中，穿刺点位置的计算采用电离层单层模型［5］，取电离层单层高度H =350 km、VTEC 模型参数nmax=2、mmax=3。

3 电离层电子总含量全天模型的建立与分析

为了了解电离层电子总含量全天变化规律，将一天分成6 个时段，分别对每个时段内的电离层TEC 进行拟合。在每个时段内，采用VTEC 多项式模型，一天内对应卫星和接收机的组合硬件延迟采用同一个参数［6］。这样，其参数设置由两部分组成:①6 个时段的电离层多项式模型系数，共6 ×3 ×4 =72 个参数;②卫星和接收机组合的硬件延迟，一般为29 个参数。则待估的参数一般为72 +29 =101。

本文利用观测文件和GPS 卫星的精密星历，计算了2006年4月10日北京房山站GPS 跟踪站单站电离层延迟模型，再利用模型系数计算了北京附近某地理经纬度(40°N，116°E)上空全天的电离层TEC日变化曲线，如图1所示。

图1 电离层TEC日变化曲线

从图1可以看出，电离层总电子含量最大值出现在地方时13 时左右，最小值出现在凌晨5 时左右(北京地方时比世界时晚8 h)。由于是分时段建立电离层延迟模型，再加上模型参数设置上自身的缺陷和观测值的精度影响，在两个相邻的时段间，模型计算的总电子含量会出现跳跃，使得总电子含量曲线图出现不连续现象。

为了克服这一不足，本文加入了在时间段的节点处函数模型值相等这一约束条件。即把多项式模型看成穿刺点经度、纬度和时间的函数:

其中B、L 分别为穿刺点的纬度和经度，t 为观测时间，i 为时段号。

在两个时段之间，要保持它在空间上的连续性和光滑性，则需要函数在空间所有点上的VTEC 值在时段间的节点处相等，这在建模时是不可能实现的。本文的计算中，选择在站点上空设置一个网格，网格大小为1° ×1°或30' ×30'，即4 个点，让函数模型6 个时段的衔接时刻，在网格点满足下面条件:

式中，(Bg，Lg)为格网点的坐标，t 为时间段衔接处的时间。

这样，共有5 ×4 =20 个限制条件，采用附有限制条件的间接平差方法，对模型参数进行求解。根据观测方程和约束条件，可以写出误差方程和限制条件为:

其中n 为观测量的个数，u 为参数的个数，s 为约束条件的个数。根据式(6)可知，约束条件Cj=(… ai，1…ai，12－ai，1…－ai，12…)，Wx=0。

由上述误差方程和限制条件，按附有限制条件的间接平差理论，可得到:

因为Wx= 0，只需计算并且约束条件C 也是一个稀疏矩阵，在构造Ncc时可以按分块构造的方法。利用上面模型重新计算北京某地全天的电离层TEC日变化曲线，结果如图2所示。

图2 带限制条件的TEC日变化曲线

从图2可以看出，在时间段衔接处的连续性有了一定提高，但还不是很光滑。为了让总电子含量连续，并且保证曲线图的精度，在时间段的衔接处取前后两个模型的内插值和外推值的加权平均值。具体的做法是在每个时间段衔接处的前后25 个历元，用下面公式计算该时刻的总电子含量，其中前一个公式用于计算时间段衔接处前25 个历元的总电子含量，后一个公式用于计算时间段衔接处后25 个历元的总电子含量:

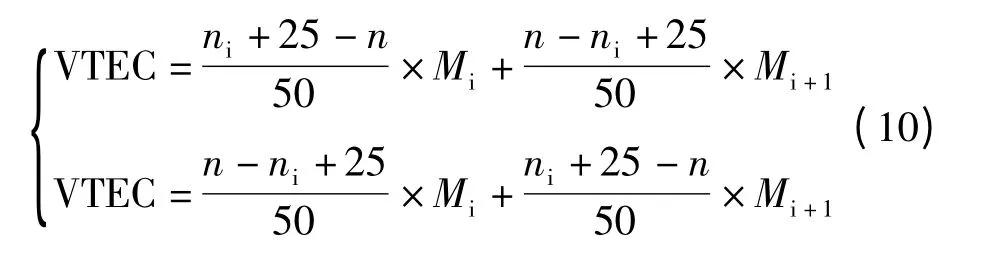
式中，n 表示该时刻的历元;ni表示第i 个时间段衔接处的历元;Mi表示第i 个模型计算得到的总电子含量。

利用式(10)和带限制条件模型重新计算全天某处的总电子含量，曲线图如3 所示。

图3 平滑后TEC日变化曲线

平滑后的曲线保持前面的TEC日变化曲线的特点，并且连续性和平滑性均得到改善，可以用于对TEC日变化规律进行研究。

4 小 结

通过试例可以看出，本文采用的增加已知条件和模型间取加权平均值的方法，能够很好地反映电离层电子总含量的实际情况，并能较好保证模型分段处的连续性。但是，本文增加的已知条件较为简单，最后也只用了加权平均的方法来提高连续性。今后可在增加约束条件个数和对约束条件求导等方面再做研究。

［1］章红平，平劲松，朱文耀等．电离层延迟改正模型综述［J］．天文学进展，2006，21(1):35 ～41．

［2］李征航，黄劲松．GPS 测量与数据处理［M］．武汉:武汉大学出版社，2005．

［3］张小红，李征航，蔡昌盛．用双频GPS 观测值建立小区域电离层延迟模型研究［J］．武汉大学学报·信息科学版，2001，26(2):140 ～143．

［4］Paulo de Oliveria Camargo，Joao Francisco Galera Monico．Application of ionospheric corrections in the equatorial region for L1 GPS users［J］．Earth Planets Space，2000，52(5):1083 ～1089．

［5］李征航，赵晓峰，蔡昌盛．利用双频GPS 观测值建立电离层延迟模型［J］．测绘信息与工程，2003，28(1)．

［6］袁运斌，欧吉坤．GPS 观测数据中的仪器偏差对确定电离层延迟的影响及处理方法［J］．测绘学报，1999，28(2):15 ～22．