基于τ- p变换的地震道重构
谢小国
(四川中成煤田物探工程院有限公司,成都 610072)
基于τ- p变换的地震道重构
谢小国
(四川中成煤田物探工程院有限公司,成都 610072)
基于τ-p变换原理,研究一种基于τ-p变换的地震数据重构方法,运用该方法对待重构道用零道替代,通过τ-p正反变换及一定的迭代处理实现地震道数据重构。理论模型与实际资料应用表明,基于p-τ变换的地震道重构方法效果明显,重构数据稳健。
τ-p变换;地震数据重构;迭代处理
实际地震数据采集过程中,测线上表现出的记录道的道间距过大或不均匀分布的现象很常见,表现为丢道、丢炮和含有强烈的空间假频。对于含有强烈噪音的地震数据,在预处理时对其进行切除,会不可避免地造成有效数据缺失。丢道、丢炮现象不仅会丢失一些重要的地下信息,同时会产生大量不必要的干扰噪音。这为地震资料数据处理的后续工作带来了许多不便。
现在已经提出多种用于缺失数据重构的方法[1-6],但这些方法一般要求动校正速度比较精确,同时当有噪音或倾斜同相轴存在时,可能会产生假同相轴。本文研究一种基于τ-p变换的地震道重构方法,既能很好地恢复缺失地震道,又能避免确定同相轴问题。
1 τ-p变换原理
τ-p正变换是一种倾斜叠加的过程,通过将xt-域中在一条斜率为p的直线上的所有点的值求和,送到另一个坐标上去,得到τ-p域数据[7],其公式为:

式中
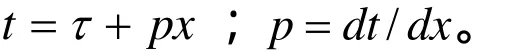
类似地,得到τ-p反变换公式

式中 pxt-=τ;dpdx/τ=。
对于离散形式的τ-p变换,正确选择τ-p变换参数非常重要,因为如果参数的选取不准,在进行τ -p变换时,会产生假频和端点效应。为了避免这些问题,射线参数p的采样必须选择准确。
根据信号理论,射线参数p的临界采样率应满足[8]
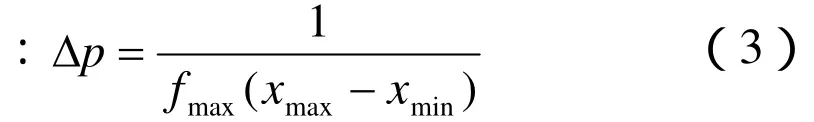
同理,射线参数p的扫描范围应满足:

式中,Δx为空间方向的采样率。
τ-p变换参数的选择应注意:
① 射线参数p不能大于pmax,否则会产生假频;②p的临界采样率不能大于公式(3)给定的值;
2 实现步骤
设待重构数据为a(t,x),则基于τ-p变换的地震数据重构方法的实现步骤如下:
1)将原始数据中待重构的道的位置用零道代替;
2)选择适当的Δp、pmax、pmin,进行τ-p正变换,得到了τ-p域数据A(τ,p);
3)由王维红[9]等提出的权系数计算方法,求取补偿系数,然后在τ-p域将数据A(τ,p)乘以一个补偿系数,得到数据B(τ,p);
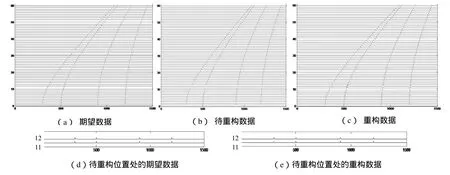
图1 重构处理模型
4)对数据B(τ,p)进行τ-p反变换,得到数据b(t,x),数据b(t,x)在数据a(t,x)为零道的位置产生了非零道;
5)用数据b(t,x)中部分重建的道数据替代数据a(t,x)中零值道,即可得到重构后的数据。
经过以上处理,就可以实现地震数据重构,如果重构效果不太好,可以重复2)到4)的过程,经过一定迭代次数,重构数据便可得到较好的实现。
3 模型验证
期望数据共60道,道长为1500ms,道间距为40m,时间采样间隔为1ms,共有四个反射层,如图1(a)。将期望数据的11、12道地震数据充零,得到待重构数据,如图1(b)。图1(c)是通过基于τ-p变换重构后的数据。待重构位置处的期望数据图1(d)与待重构位置处重构后的数据图1(e)比较可以看出,地震数据的重构效果非常好,振幅差异小,所有的相干同相轴都得到了正确的重构。
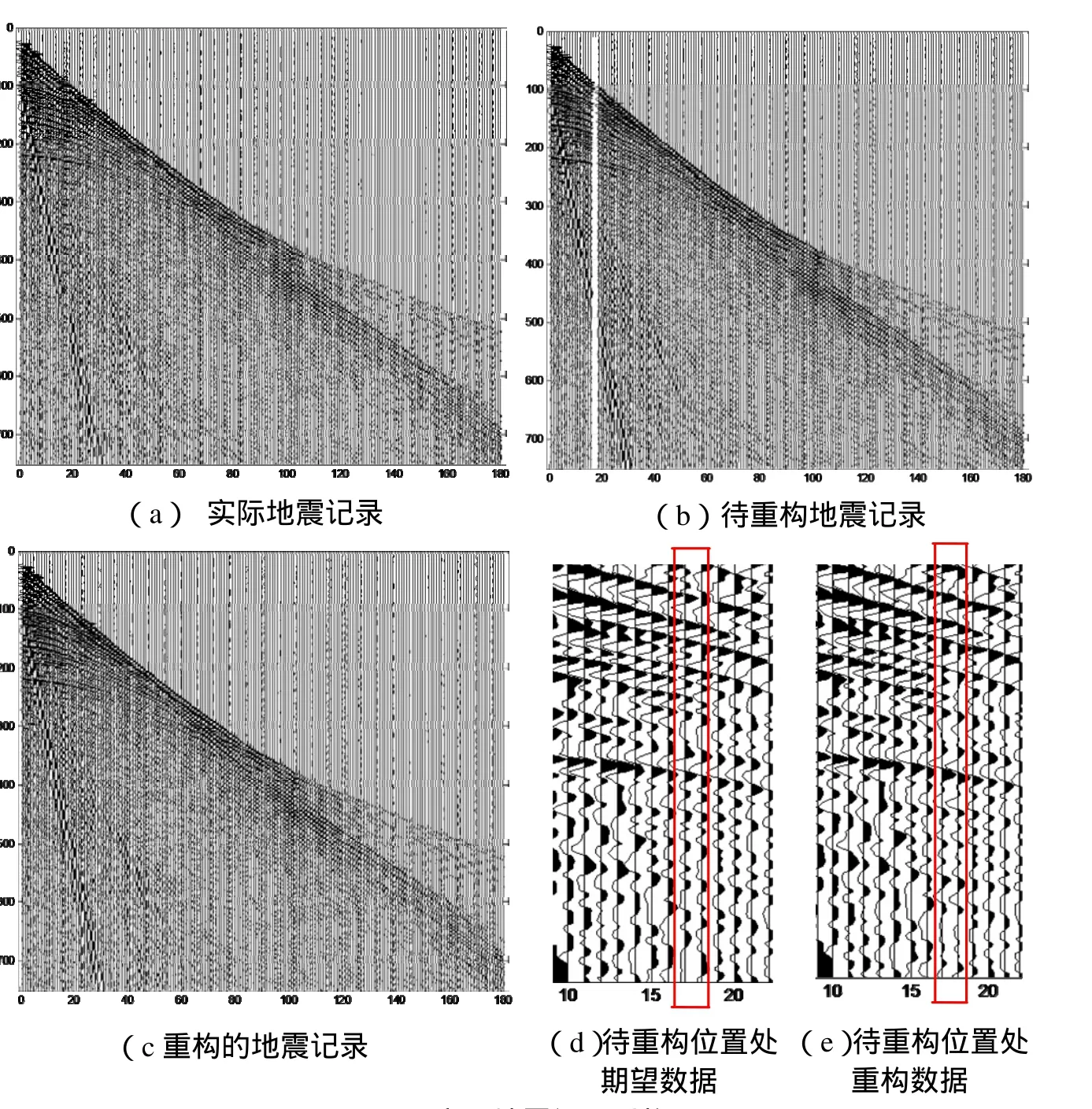
图2 实际地震记录重构
4 实际资料重构
图2(a)是实际的单炮单边地震记录,有180道,750个采样点,将其17、18道地震道抹去得到待重构数据,如图2(b),通过基于τ-p变换的地震道重构方法进行重构处理,缺失地震道基本得到恢复,如图2(c)。比较待重构位置处的期望地震数据(图2(d))与待重构处重构的地震数据(图2(e)),可以看出重构处理恢复的同相轴保持原始剖面的特征。
5 结论
基于τ-p变换的地震数据重构方法在地震数据重构方面取得了非常好的效果,除了振幅上的差异外,恢复的相干同相轴清晰、稳定,没有产生假同相轴,重构效果明显。理论上讲,该方法只适用于线性或近于线性同相轴的地震数据处理,但是对于实际资料处理研究发现,本文方法对中等复杂程度的地震记录仍然非常有效和稳定。τ-p变换的参数数据选择非常重要,如果参数选取不准,将产生假频和端点效应,严重影响重构效果。迭代处理使重构效果更明显,但迭代次数不应太多,否则计算量会相应增加。
[1] 沈操,牛滨华,等.基于信号重构的地震道插值[J].现代地质,2000,14(4):470~474.
[2] 孟小红,郭良逃,等.基于非均匀快速傅里叶变换的最小二乘反演地震数据重建[J].地球物理学报,2008,51(1):235~241.
[3] 刘红梅,刘洪.基于稀疏τ-p变换的叠后地震数据外推[J].物探化探技术,2007,29(1):1~6.
[4] 刘保童.一种基于傅里叶变换的去假频内插方法及应用[J].煤田地质与勘探,2009,37(02):63~67.
[5] 刘保童.一种基于傅里叶变换的去假频内插方法及应用[J].煤田地质与勘探,2009,37(02):63~67.
[6] Claerbout J.Interpolation beyond aliasing by(t-x) domain PEFs[J].53rd Ann Internat Mtg,Eur Assn Geosci Eng,Expanded Abstracts,paper A001,1991.
[7] 吴律.τ-p变换及应用[M].北京: 石油工业出版社,1993.
[8] 黄新武,吴律,牛滨华.基于抛物线拉东变换的地震道重构[J].中国矿业大学学报,2003,32(05):534~538.
[9] 王维红,裴江云,张剑峰.加权抛物Radon变换叠前地震数据重建[J].地球物理学报,2007,50(3):851~859.
Reconstruction of Seismic Traces byτ-p Transform
XIE Xiao-guo
(Sichuan Zhongcheng Coalfield Geophysical Engineering Institute Co., Ltd, Chengdu 610072)
Based on the principle of p-τ transform, a method for reconstruction of seismic traces is put forward. This method is taken for the data containing zero traces at the missing offset location, using iteration, adoption of forward and inverse p-τ transform to reconstruct seismic traces. The results of the theoretical model and the field data demonstrate its remarkable effect and robustness.
p-τ transform; seismic data reconstruction; iteration
P631.4
A
1006-0995(2014)04-0625-03
10.3969/j.issn.1006-0995.2014.04.035
2013-12-23
谢小国(1992—),男,四川成都人,本科,研究方向为:地球物理勘探

