空间多轨道梁线性检验的优化设计

苏京平,洪丹丹,王宣庆

(上海市岩土工程检测中心,上海 200436)

空间多轨道梁线性检验的优化设计

苏京平∗,洪丹丹,王宣庆

(上海市岩土工程检测中心,上海 200436)

大型厂房空间多轨道梁在施工和运营检测中,对单轨道本身的直线度及双轨和多轨道间的平行度都有极高的精度要求,若不达标,将对空间轨道的安全运行造成严重影响。常规的检测方案难以同时兼顾上述多项约束条件,更无通用模型可言。针对上述技术难点,我们以单轨、双轨和多轨三种不同情况为研究对象,采用平行直线拟合的方法,对空间多轨道梁线性检验的技术路线进行分析、论证,给出了检测的数学模型,并以工程实例说明设计方案的优化效果。

轨道梁;线性检验;直线拟合;平行;观测点

1 引 言

某重型设备生产车间预安装大型空间轨道梁,轨道长度约300 m,共7根轨道,轨道间距约20 m。由于轨道设计要求精密,需要在轨道正式安装前,对预装焊接托架的直线度及双线间的平行度进行实测检验,要求如下:

(1)对单轨道进行直线检验,根据检验结果,对各焊接点进行直线调整。

(2)对双轨道平行度进行检验,根据检验结果,对双轨道进行平行调整。

(3)对多轨道直线性和平行度进行检验,根据检验结果,对多轨道进行直线和平行调整。

现场根据初步定位结果预装的焊接托架仅可做微量调整,要求以满足设计精度要求为原则,尽量少调整或不调整。为此,需要根据检测数据,进行空间轨道梁多线验直的优化设计,如图2所示。

图1 检测现场实景图

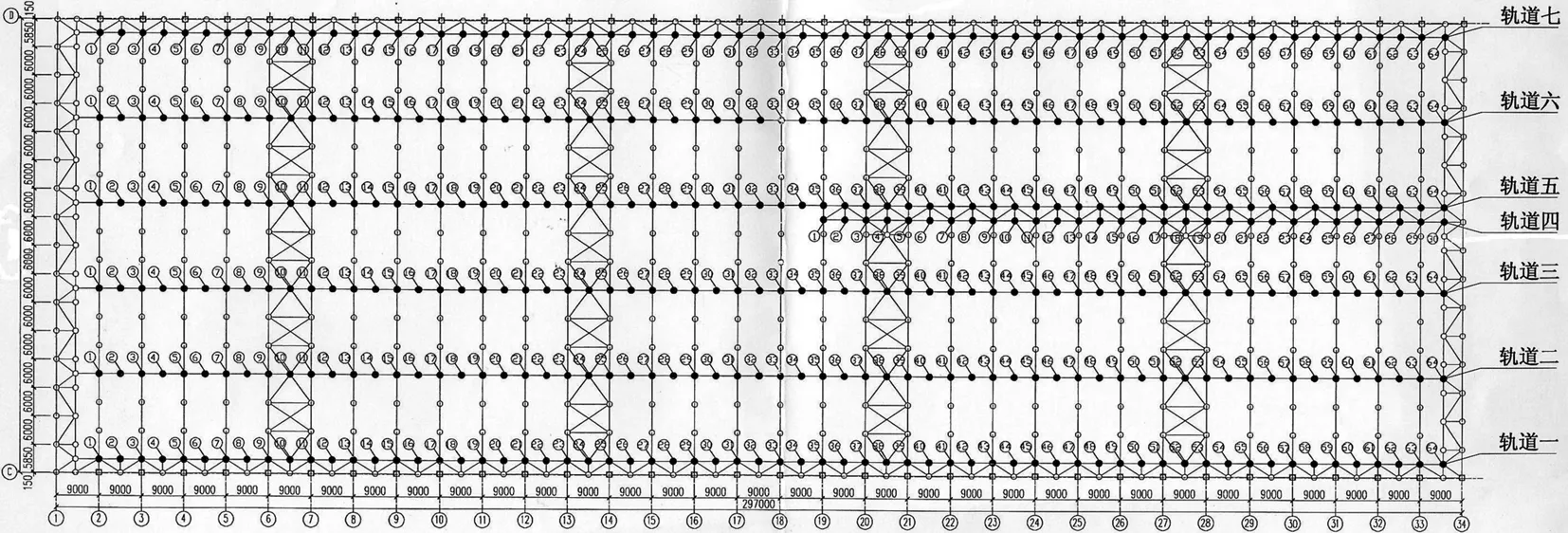
图2 轨道安装设计图

2 优化设计的数学模型

2.1 单轨道直线拟合

如图3所示,以单轨道检测点实测平面坐标构建数据组:(x1,y1),(x2,y2),…,(xn,yn)

利用上述数据拟合直线l:ax-y+b=0

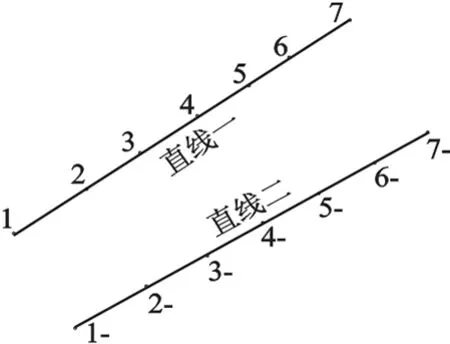
图3 轨道梁线性检验优化设计示意图

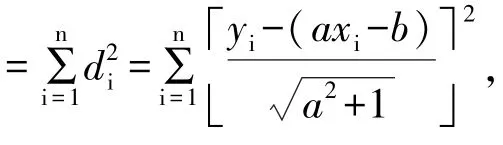
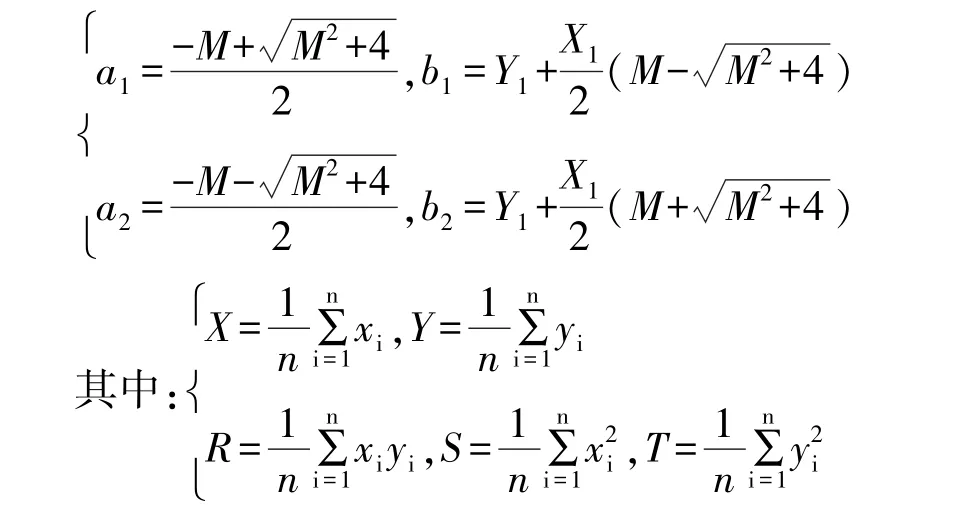
经验证,当R＞XY时,(a1,b1)是φ(a,b)的最小值点,当R＜XY时,(a2,b2)是φ(a,b)的最小值点。

2.2 双轨道平行最优设计

数据组1:(x11,y11),(x12,y12),…,(x1m,y1m)

数据组2:(x21,y21),(x22,y22),…,(x2n,y2n)

利用数据组1可拟合出直线l1:a1x-y+b1=0

利用数据组2可拟合出直线l2:a2x-y+b2=0

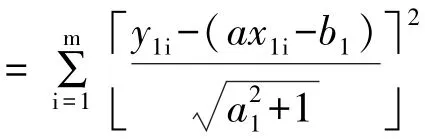
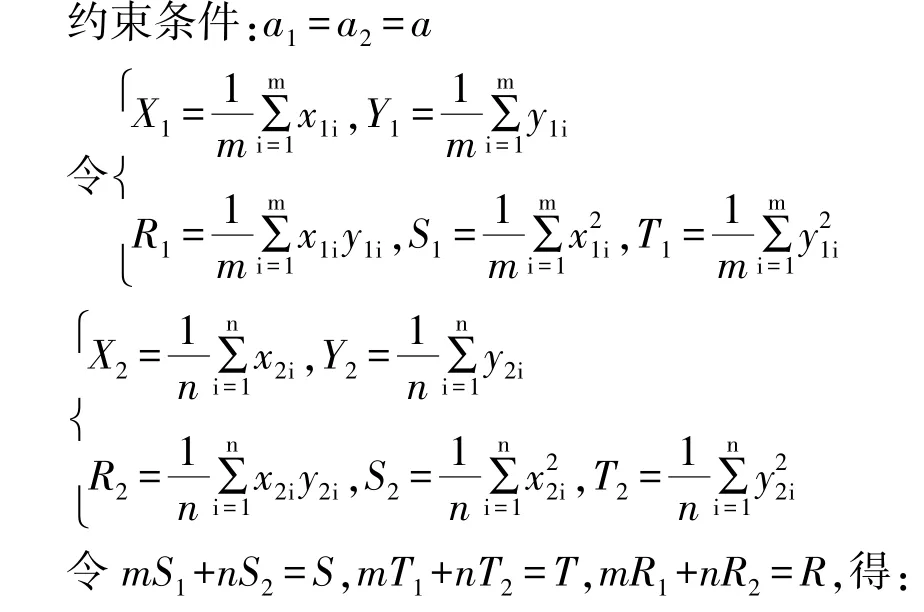
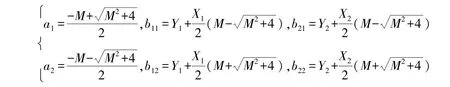
经验证,当R＞XY时,(a1,b11,b12)是φ(a,b1,b2)的最小值点,当R＜XY时,(a2,b21,b22)是φ(a,b1,b2)的最小值点。

2.3 多轨道线性检验最优设计

数据组1:(x11,y11),(x12,y12),…,(x1k1,y1k1)

数据组2:(x21,y21),(x22,y22),…,(x2k2,y2k2)

……

数据组n:(xn1,yn1),(xn2,yn2),…,(xnkn,ynkn)

根据上述数据组可拟合出n条直线l1,l2,…,ln,分别为:

a1x-y+b1=0,a2x-y+b2=0,…,anx-y+bn=0

目标函数:

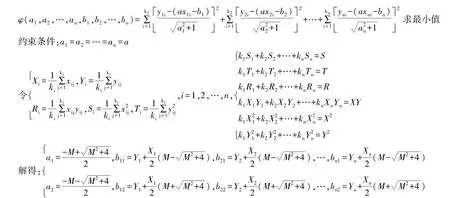
经验证,当R＞XY时,(a1,b11,b12,…,b1n)是φ(a,b1,b2,…,bn)的最小值点,当R＜XY时,(a2,b21,b22,…,b2n)是φ(a,b1,b2,…,bn)的最小值点。

3 计算实例

3.1 实测数据

为更有效和直观地表达多轨道梁线性检验的技术思路,限于篇幅,本文以两条特例(预装的焊接托架误差偏大)轨道的最优设计为例,演示计算结果。表1为两轨道梁调线前现场测量的结果。

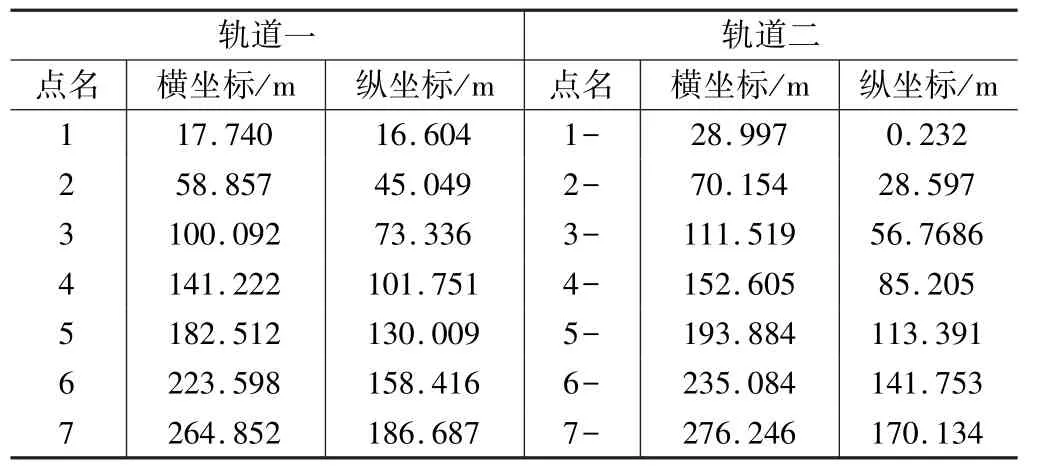
表1 轨道检测成果表

3.2 设计结果

采用MATLAB软件,依据上文设计思路进行如下运算:

(1)利用轨道一实测数据可拟合出直线l1:

a1x-y+b1=0,式中:a1=0.687 5,b1=4.566 2

(2)利用轨道二实测数据可拟合出直线l2:

a2x-y+b2=0,式中:a2=0.687 5,b2=-19.792 4

双线线性检验的设计输出结果如图4所示:

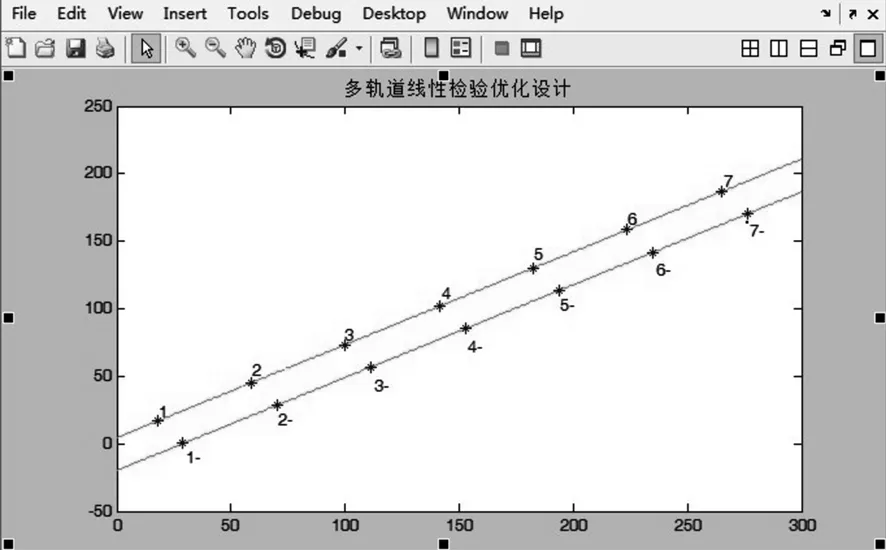
图4 双轨道梁线性优化设计图

3.3 直线调整

根据优化设计输出的轨道梁最优直线位置,对预装的焊接托架实际点位进行调整,结果如表2所示:

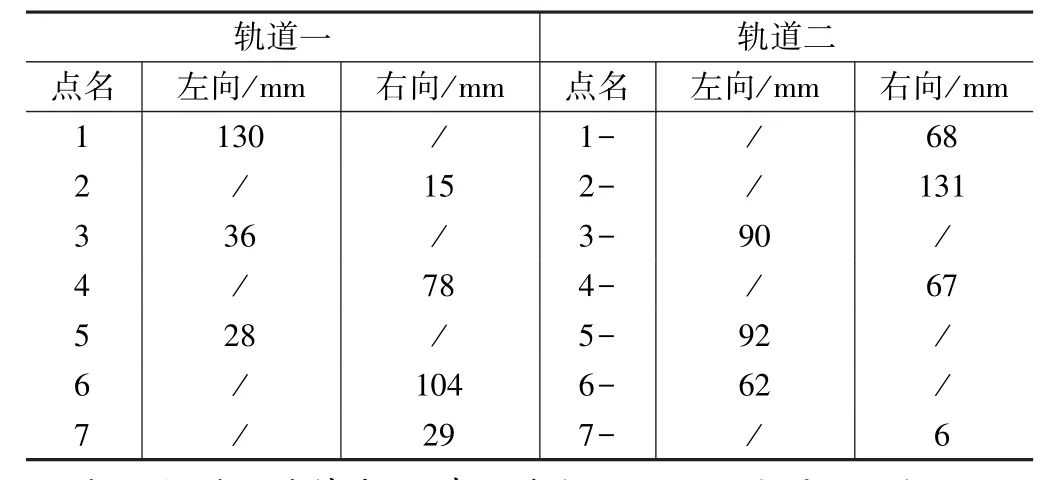
表2 轨道调线成果表

4 结论与建议

(1)采用直线拟合原理,根据实际检测数据设计多轨道最优调整方案,理论严密,可操作性强,为同类工程实践提供指导,具有较好的推广价值。

(2)文中直线拟合采用点到直线距离平方和最小并附加直线斜率相等的条件,比单一方向的线性拟合更加合理。

(3)轨道梁实测数据的精度直接关乎优化设计方案的成败,因此,现场检验施测必须掌握作业关键步骤和要领。

[1] 同济大学应用数学系主编.高等数学(第五版)[M].高等教育出版社,2003.

[2] 李青岳,陈永奇.工程测量学[J].北京:测绘出版社,1995.

[3] GB/T 15314/1994.精密工程测量规范[S].

[4] GB 50205-2001.钢结构工程施工质量验收规范[S].

[5] GB 50278-2010.起重设备安装工程施工及验收规范[S].

Optimization Design on Linearity Test of Spatial Multi-Track Beams

Su Jingping,Hong Dandan,Wang Xuanqing
(Shanghai Geotechnical Engineering Detecting Centre,Shanghai 200436,China)

There are high accuracy requirements for the straightness of single track and for the parallelism of double and multi-tracks during the precision construction and operational testing of spatial multi-track beams in large factory.If the requirements were not met,the safe operation of spatial tracks might be seriously impacted.The normal tests are difficult to meet all these constraints,needless to say the general model.Aiming at the technical difficulties above,three different cases of single track,double track and multi-track are studied.The method of parallel linear fitting is adopted to analyze and demonstrate the technical route of spatial multi-track beams.The testing mathematical model is given,with one engineering example illustrating the optimal design scheme.

track beams;linearity test;linear fitting;parallel;observation point

2014—02—17

苏京平(1966—),男,注册测绘师,高级工程师,主要从事测绘技术管理工作。