基于全变差重构算法的数字全息研究

简献忠，周 海，乔静远，李 莹，王 佳

基于全变差重构算法的数字全息研究

简献忠，周 海，乔静远，李 莹，王 佳

（上海理工大学光电与计算机学院上海现代光学系统重点实验室，上海200093）

为了消除传统算法对数字全息重构过程中会出现0级像、共轭像干扰的问题，将压缩感知理论与数字全息图再现相结合，提出了基于全变差的两步迭代收缩阈值重构算法（TwIST），并应用于数字全息图压缩感知全息图重建。TwIST算法根据重构成分的特点增加正则约束，对相应的形态进行调整，在满足全变差最小的特性的基础上进行重构，提高了重构全息图的质量。结果表明，TwIST算法可以对数字全息图稀疏重建，利用35%的部分全息图数据进行图像重构，重构图像峰值信噪比为36.46dB，且没有0级像和共轭像等干扰。该研究结果对实现计算全息的实时性具有重要的意义。

全息；压缩感知；计算全息；数字全息图；全变差重构算法

引 言

数字全息是用CCD等光电探测器件代替全息记录材料记录全息图，然后通过计算机用数字仿真的方法再现全息图［1］。与传统全息相比，这一方法制作成本低、成像速度快、具有明显的简易性和灵活性等特点［2-4］。经过多年的发展，出现了大量对数字全息重建的算法。传统的数字全息重建算法［5-6］在重建过程中会出现0级像和共轭像等干扰的问题，而且重构过程都是对全息图的全部数据进行的，因而存在较大的计算冗余［7］。

压缩感知是近年来在信息处理领域中对传统奈奎斯特抽样理论的重要推广和发展。它是CANDES，ROMBERG及华裔科学家TAO等学者在稀疏表示和优化理论的基础上提出的信号重建理论［8-9］。直接将采样与压缩相结合，对稀疏或可压缩的高维信号投影成的低维信号进行测量，然后通过最优化问题求解实现对原始高维信号的精确重构，这就是压缩感知理论的本质。近年来，为了解决数字全息中重构图像质量的问题，有研究者开始把压缩感知理论应用到全息中。MARIM等人［10］将压缩感知理论用于全息显微镜中，实现了在噪声干扰下稀疏采样重建微小物体的形状。参考文献［7］中说明了压缩感知理论能够很好地应用于数字全息，参考文献［11］中采用正交匹配追踪算法对全息图进行重构，但是重构效果还待提高。

作者在分析了压缩感知的原理和应用方法的基础上，提出了基于全变差的两步迭代收缩阈值重构算法，利用该算法对计算机模拟的数字全息图的部分数据采样进行重构，得到了较高质量的重构图像，为实现全息实时显示提供了一种新的技术途径。

1 压缩感知的基本理论

压缩感知理论主要是从信号的稀疏表示、测量矩阵构造和算法重构这三部分来描述的。

1.1稀疏表示

考虑长度为n的离散信号x，可以用一组标准正交基Ψ1，Ψ2，…，Ψn线性表示，则该信号表示为：

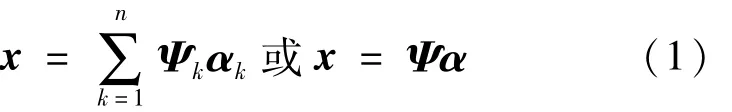
显然α是信号在Ψ域的表示，这里k＝1，2，…，n。

运用压缩感知理论的关键问题取决于该信号是否具有稀疏性或者近似稀疏性，若（1）式Ψ中的α只有k个非零值（n≫k），可认为信号是稀疏的。离散信号x能够被精确重构的前提是系数向量α是系数的，即Ψ域是稀疏域，需要选择合适的基来表示信号，才能使信号有足够的系数以保证能够精确重构。光滑信号的傅里叶系数、傅里叶小波系数等都具有足够的稀疏性，均可以作为信号的稀疏基。

1.2测量过程

用一个与变换矩阵不相关的m×n（m≪n）矩阵Φ对信号进行线性投影，可以得到线性测量值y：

测量值y是一个m×1矩阵，这样使测量对象从n维降为m维。将（1）式带入（2）式中，有：

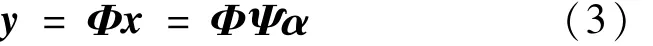
式中，Φ为感知矩阵或测量矩阵。要保证可压缩信号x从n维降到m维的过程中主要信息不丢失且能够准确重建出原始信号，还要保证测量矩阵和稀疏基不相关性、测量次数m＝O［klg（n）］和测量矩阵满足约束等距准则（restricted isometry property，RIP），O为计算复杂度的运算符。

1.3重构算法

目前，基于压缩感知理论的重构算法主要包括最小l1范数法、匹配追踪系列算法、迭代阈值法以及专门处理2维图像问题的最小全变分等。这些算法都是基于两种求解模型：l0求解模型和l1求解模型［12］，如下所示：

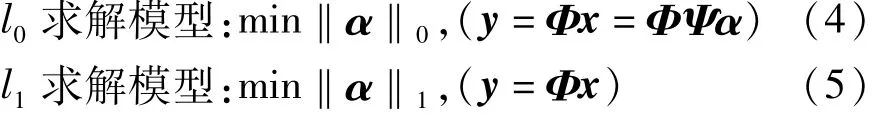
式中，‖α‖0为向量α的l0范数，表示α中非零元素的个数；‖α‖1为向量α的l1范数。

2 全变差的两步迭代收缩阈值重构算法

［7］中分析了压缩感知框架数字全息重构方法的可行性，采用全变差求整个空间内梯度l1范数，实现数字全息的重建。为了提高图像的重构速度和质量，参考文献［13］中提出了两步迭代收缩阈值重构算法（two-step iterative shrinkage thresholding，TwIST）。在感知图像重构中，为了提高重构图像的质量，可以根据不同成分的特点增加正则约束，对相应的形态成分调整。除了稀疏表示的先验条件以外，图像平滑成分和边缘轮廓成分通常还满足全变差最小的特性，所以本文中在使用两步迭代收缩阈值重构算法同时加入全变差最小正则项，进一步来改善重构成分的质量。

将（4）式转化为凸规划的l1范数求解，变形为带有拉格朗日乘积的形式，求解目标函数取最小值的系数问题：

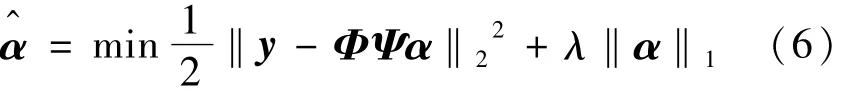
把全变差最小的约束加入重构算法中，（7）式变为：

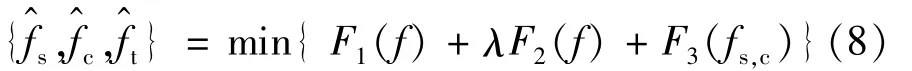
式中，F3（fs，c）＝∑k＝s，cV（fk），V（fk）表示全变差。

将V（fk）加入重构方程，基于全变差TwIST重构算法步骤如下所示，简记：Tk，λ（x）＝Ψk｛Tλ［ΨkT（fk，j＋ΦTx）］｝，（k＝s，c，t），Tλ为阈值函数；Gk，h（x，y，u，p，q）＝（1－γ）x＋（γ－β）y＋βTk，λ×，其中γ和β为决定算法收敛速度的参量参量的设定为：步参量μ＝1；阈值步长h＝1；迭代终止值为ε。

（1）初始化，迭代次数为j＝0，重构图像为f0＝fk，0＝fVs，0＝fVc，0＝0，最大迭代次数为jmax。

（2）更新第1次迭代数据：j＝j＋1。

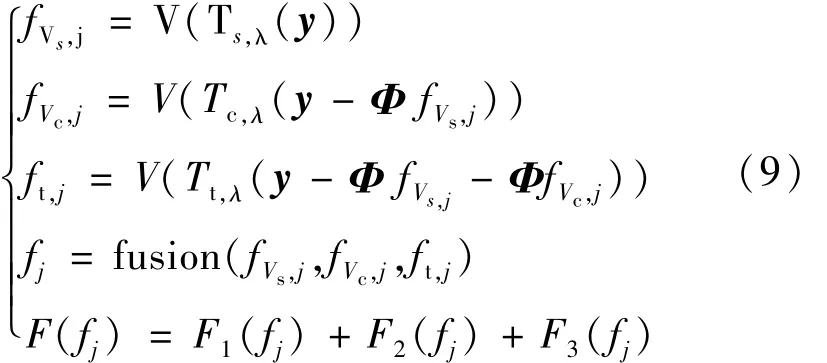
（3）更新第j＋1次的迭代数据：

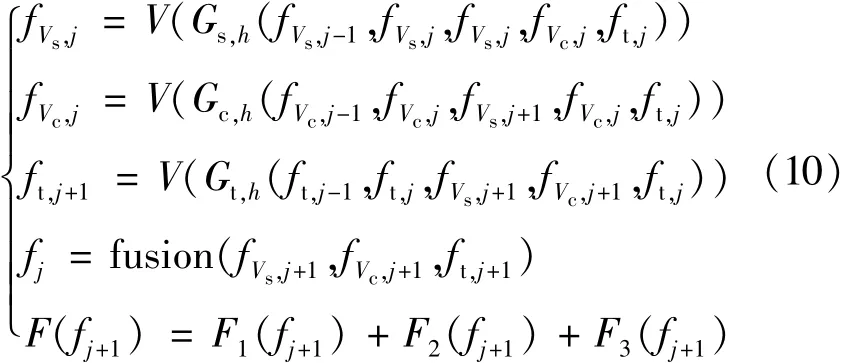
（4）对两次目标函数值进行比较，若F（fj＋1）＞F（fj），则h＝2h，返回第（3）步，否则继续下一步。

（5）判断是否满足终止条件，若j＋1＝jmax，则终止迭代，输出重构图像fj＋1，否则更新迭代次数j＋1，转至第（3）步继续执行。

3 实验仿真与对比

3.1数字全息重构实验

在实验中，使用Mach-Zehder干涉仪实验装置获取一幅“N”字母的全息图，Mach-Zehder干涉仪实验装置如图1所示。重构采用PC平台，硬件为英特尔G630 2.70GHz、内存2G，软件为Windows XP，MATLAB R2010a版本。图2a是CCD拍摄的全息图；图2b是卷积算法重构的图；图2c是快速傅里叶逆变换重构的图；图2d是全变差TwIST算法重构的图。

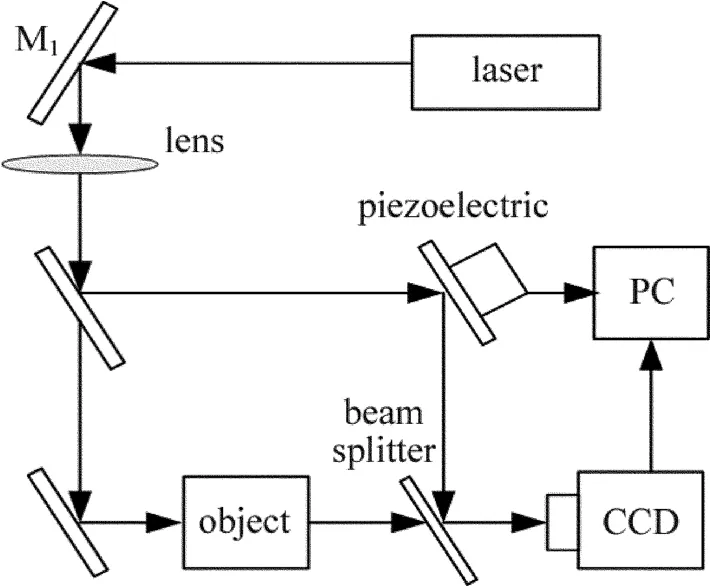
Fig.1 The Mach-Zehder interferometer experimental setup

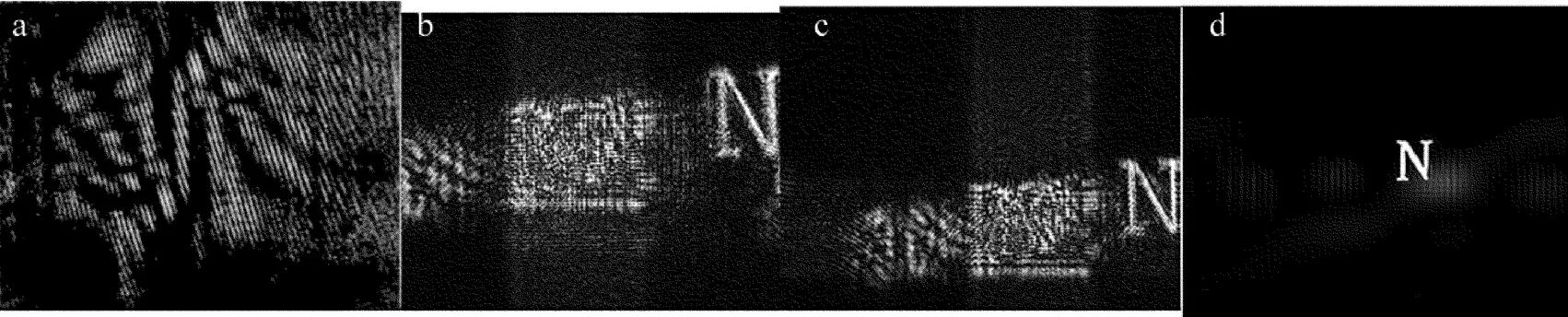
Fig.2 Digital hologram and the reconstructed image

3.2数值模拟重构实验

为了进一步说明该算法的特点，对标准测试图进行数值模拟实验。首先产生数字全息图，模拟物光波振幅和数字全息图均为256灰度级的256pixel× 256pixel图像，如图3a、图3b所示；图3c是卷积算法重建的图像；图3d为正交匹配追踪（orthogonal matching pursuit，OMP）算法重构的图像；图3e是全变差TwIST算法重构的图像。

Fig.3 The simulation of digital hologram and the reconstructed image

通过对图2d和图2b、图2c进行对比，说明了压缩感知对数字全息图重构的可行性，而且压缩感知算法重构的图像明显没有0级像和共轭像，可重构出高质量的图像，说明本文中提出的全变差TwIST算法能够高质量地重构图像。

通过对图3d、图3e和图3c进行对比，说明了35%的数字全息图压缩感知重构的图像质量明显优于100%数字全息图传统算法重构图像的质量，显示了所有细节；对图3d和图3e进行对比，OMP算法重构图像峰值信噪比（peak signal-to-noise ratio，PSNR）为26.16dB，而全变差TwIST算法重构图像的PSNR值为36.46dB。

4 结 论

实验结果表明，TwIST算法能够应用在数字全息图的重构，重构了高质量的再现像，PSNR值为36.46dB，消除了传统重构图像中出现的0级像和共轭像的问题，显示了所有细节，峰值信噪比高。在全变差TwIST算法重构过程中，原始物体本身的透射重构是直接通过数字全息图获得的线性观测向量和传感矩阵得到的，同时使用最小全变差约束可以使得图像在重构过程中更为稀疏，进而有助于消除图像边缘伪影对重构结果所带来的干扰，因此获得了高质量的重构图像。

TwIST算法能够应用在数字全息图的重构，仅用35%的全息图数据重构了高质量的再现像，这实现了全息图数据的压缩，减少了数据采集量和计算冗余，为计算全息实时显示提供了一种新的技术途径。

参考文献

［1］ JIAN X Z，ZHANG H，FAN JP，et al.Research of computergenerated hologram based on FPGA technology［J］.Laser Technology，2011，36（1）：26-32（in Chinese）.

［2］ CHEN N.Research on digital holography［D］.Guangzhou：Jinan University，2004：58-80（in Chinese）.

［3］ FENG Y J，DING JP，ZHOU J.Self-focusingmatched filter produced by computer-generated hologram［J］.Optics Communications，2000，184（1）：89-93.

［4］ YU Z L，JING F.Computer generated hologram［M］.Beijing：Tsinghua University Press，1984：1-194（in Chinese）.

［5］ SONG X F，ZHAO BQ，QIN A.Comparison of three basic reconstruction algorithms in digital holography［C］／／Optical Test and Measurement Technology and Equipment.Chengdu：International Society for Optics and Photonics，2009：40-46.

［6］ LI JC.FFT computation of angular spectrum diffraction formula and its application in wavefront reconstruction of digital holography［J］.Acta Optica Sinica，2009，29（5）：1163-1167（in Chinese）.

［7］ WU Y C，WU X C，WANG Z H，et al.Reconstruction of digital inline hologram with compressed sensing［J］.Acta Photonica Sinica，2011，31（11）：1109001（in Chinese）.

［8］ CANDESE J，ROMBERG J，TAO T.Robust uncertainty principles：exact signal reconstruction from highly incomplete frequency information［J］.IEEE Transactions on Information Theory，2006，52（2）：489-509.

［9］ CANDESE J，TAO T.Near-optimal signal recovery from random projections：universal encoding strategies［J］.IEEE Transactions Information Theory，2006，52（12）：5406-5425.

［10］ MARIM M M，ATLAN M，ANGELINIE D，et al.Compressed sensing for digital holographic microscopy［C］／／Biomedical Imaging：From Nano to Macro，2010 IEEE International Symposium.Rotterdam，Holland：IEEE，2010：684-687.

［11］ MA JSh，XIA F P，SU P，et al.Study on compressive sensing phase-shifting digital holography［J］.Semiconductor Optoelectronics，2013，34（1）：130-133（in Chinese）.

［12］ CHEN SSh B，DONOHO D L，SAUNDERSM A.Atomic decomposition by basis pursuit［J］.SIAM Review，2001，43（1）：129-159.

［13］ BIOUCAS-DIAS JM，FIGUEIREDOM A T.A new TwIST：twostep iterative shrinkage／thresholding algorithms for image restoration［J］.IEEE Transactions on Image Processing，2007，16（12）：2992-3004.

Study on digital holography based on the total variation reconstruction algorithm

JIANXianzhong，ZHOUHai，QIAOJingyuan，LI Ying，WANGJia
（Shanghai Key Laboratory of Modern Optical System，Electrical Engineering College，University of Shanghai for Science and Technology，Shanghai200093，China）

In order to eliminate the zero-order image and the conjugate image interference problems in the traditional algorithm for reconstruction of digital hologram，a new algorithm based on the total variation of the two-step iterative shrinkage thresholding（TwIST）was proposed combining compressive sensing theory with reconstruction of the digital hologram.According to the characteristics of the reconstruction component，the TwIST algorithm based on the total variation improves the quality of the reconstruction of hologram.The simulation results show that the hologram can be reconstructed from a sparse hologram with TwIST reconstruction algorithm a high quality image was reconstructed from 35%of a hologram and the peak signal-to-noise ratio（PSNR）of the reconstructed image was36.46dB without zero-order image and conjugate image interference.The study is helpful for implementing real-time computer-generated hologram.

holography；compressive sensing；computer-generated hologram；digital hologram；total variation reconstruction algorithm

O438.1

A

10.7510／jgjs.issn.1001-3806.2014.02.019

1001-3806（2014）02-0236-04

上海市高等学校建设基金资助项目（2009014）；上海市研究生创新基金资助项目（JWCXSL1302）

简献忠（1969-），男，副教授，博士，主要从事数字全息、嵌入式技术应用等方面的教学与科研工作。

E-mail：jianxz＠usst.edu.cn

2013-04-23；

2013-06-03