瑞利多普勒激光雷达F-P标准具的设计与校准分析

唐 磊，吴海滨，孙东松，舒志峰

瑞利多普勒激光雷达F-P标准具的设计与校准分析

唐 磊1，吴海滨2*，孙东松3，舒志峰3

（1.合肥师范学院物理与电子工程系，合肥230031；2.安徽大学物理与材料科学系，合肥230031；3.中国科学技术大学地球与空间科学学院，合肥230031）

为了精确观测平流层风场，采用F-P标准具作为瑞利散射测风激光雷达多普勒频率检测的核心器件，对F-P标准具多普勒频率检测原理进行了理论分析，从分析最大设计高度时的测量误差着手，优化选取标准具透过率曲线参量；介绍了透过率曲线参量的校准过程和校准方法，分析了导致透过率曲线的半峰全宽增大的原因、透过率曲线校准精度对速度灵敏度及系统探测误差的影响；并通过实验对设计和校准结果进行了验证。结果表明，由于透过率曲线的半峰全宽增大，导致速度灵敏度下降了0.118%／（m·s－1）；40km高度处，在测量信噪比大于10的条件下，径向速度测量精度增大2m／s。

激光技术；激光雷达；Fabry-Perot标准具；瑞利散射；多普勒频率

引 言

非相干多普勒激光雷达系统提供了一种从近地面到平流层矢量风场测量的方法。通过分析激光在大气中传输的后向散射信号获得多普勒频移信号，从而确定径向风速。利用Fabry-Perot（F-P）标准具检测的多普勒测风激光雷达可以同时检测激光在大气传输过程中的气溶胶及分子后向散射信号，能够提供高时空分辨率、高测量精度的风场数据，对高能激光大气传输研究、空间范围的战略防御和进攻系统及提高分析全球气候变化的能力都有非常重要的促进作用；还能进一步深入对大气动力学和全球大气运动，以及对能量、水、气溶胶、化学和其它空气物质圈的了解。尤其对于平流层风场测量，除了它在气候变化中的重要地位及广泛的应用领域，对其本身的研究也在不断增加。更重要的是，瑞利散射提供了一个全球范围的、可靠且相对稳定的散射源，包括极地和海洋，使得中高层全球大气风场探测成为可能［1］。

在利用F-P标准具检测的瑞利散射多普勒测风激光雷达系统研制过程中，F-P标准具作为瑞利散射多普激光雷达频率检测的核心器件，其透过率曲线参量的优化设计及校准精度直接影响激光雷达的系统性能。据此，本文中分析了F-P标准具参量的优化选取，提出了F-P标准具透过率曲线的详细校准过程及方法，分析了校准误差产生的原因及对系统测量误差的影响。

1 瑞利散射光信号的多普勒检测原理

利用双边缘技术测量激光后向瑞利散射信号通过标准具的透过率变化，可以反演出信号的多普勒频移。由于瑞利散射谱与发射激光谱相比宽很多倍，因此，需要利用速度灵敏度较高的双F-P标准具的结构。这时标准具的两个边缘通道的透过率边缘分别位于瑞利散射谱的两翼，如图1所示。瑞利后向散射信号光通过两个标准具时，由于风速引起的多普勒频移信号的频谱中心相对发射激光频率发生移动，两个标准具的输出信号产生差异，根据这个差异的大小可以反演出频率移动的量，即多普勒频率［2-3］。多普勒频移同样引起气溶胶散射谱相对激光发射频率发生移动，两个边缘通道接收的信号光强不同，因此需要考虑气溶胶散射的影响［4］。

Fig.1 Doppler frequency measurement based on Rayleigh backscattered signal

当标准具对瑞利散射光信号的速度灵敏度等于标准具对米散射光信号的速度灵敏度时，多普勒测量结果由发射激光信号和接收信号光通过标准具两个通道的光强度之比决定。在这种情况下，气溶胶散射信号不是作为噪声处理的，而是可以利用的有用的测量信号，相当于同时利用分子散射和气溶胶散射信号进行大气风速的测量［5-9］。可求得多普勒频移量为：

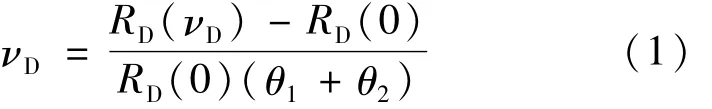
式中，νD为多普勒频率，θ1，θ2为边缘通道1和2的速度灵敏度，RD（）为对应多普勒频率的响应函数。

径向速率为：

式中，v表示径向速率，λ为发射激光波长。径向风速的误差为：

式中，θ＝θ1＋θ2是双边缘测量总的速度灵敏度，S／N是双边缘测量的信噪比，它由下式给出：

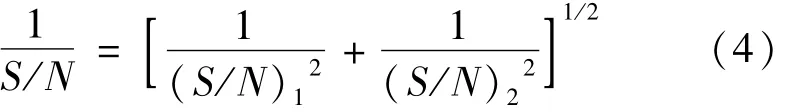
式中，（S／N）i是第i个通道信号Ii的信噪比。

2 F-P标准具参量优化设计

瑞利散射的强度一般随高度减小，散射信号的谱宽随温度降低或高度增加而变窄。因此，在考虑F-P标准具的参量时，应从系统设计的最大高度的平均大气温度和信号条件下的测量误差分析出发。考虑在散粒噪声限下信噪比与信号接收光子数的平方根成正比，于是探测误差只与标准具的速度灵敏度和通过标准具的瑞利信号有关，根据激光器的参量，即波长355nm、频谱宽度200MHz，给出测量的相对误差与F-P标准具的谱宽和谱中心相对激光发射频率位置的曲线，如图2所示。图中显示了30km（T＝226K）高度处优化相对误差随参量offset在不同标准具宽度下的变化情况。相对误差随着参量offset的增大迅速下降，从2GHz到曲线最低点误差下降了近两倍；随着标准具频谱分辨率的降低误差缓慢变小，在1.7GHz时相对误差达到最小。还可以看出频率在4.0GHz～5.2GHz时误差变化相对平缓，根据误差最小原理选择标准具的半峰全宽（full width at half maximum，FWHM）为1.7GHz，但峰值位置的确定还要综合考虑气溶胶散射信号的影响［10-11］。

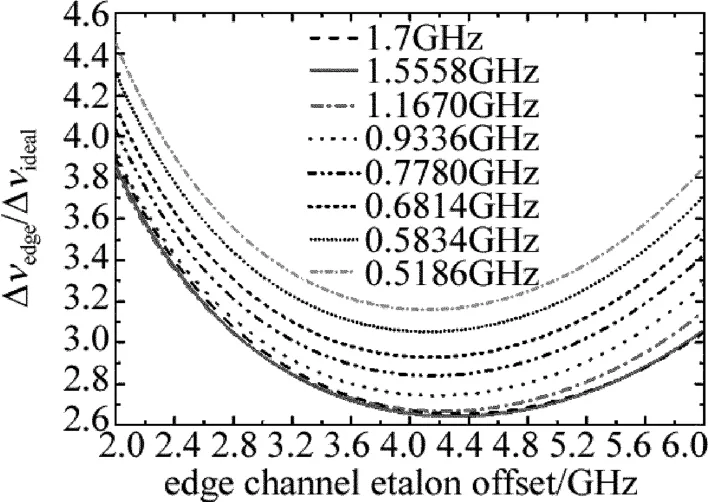
Fig.2 Relative errors for various etalon spectral widths as a function of the separation between two edge-channels of the etalon

基于瑞利散射和气溶胶散射的速度灵敏度函数曲线如图3所示。在气溶胶和分子散射的速度灵敏度交叉点处，测量的多普勒频移结果不受气溶胶散射的影响，因为单位速度变化引起的气溶胶和分子散射信号强度变化相等。图中选取的标准具半峰全宽为1.7GHz，在两条灵敏度曲线的交点处，即两者灵敏度相等，两个边缘通道标准具的谱峰值间距为标准具谱宽的3.02倍，即5.1GHz。从图2可以看出，该参量也基本满足误差最小的条件［3-5］。

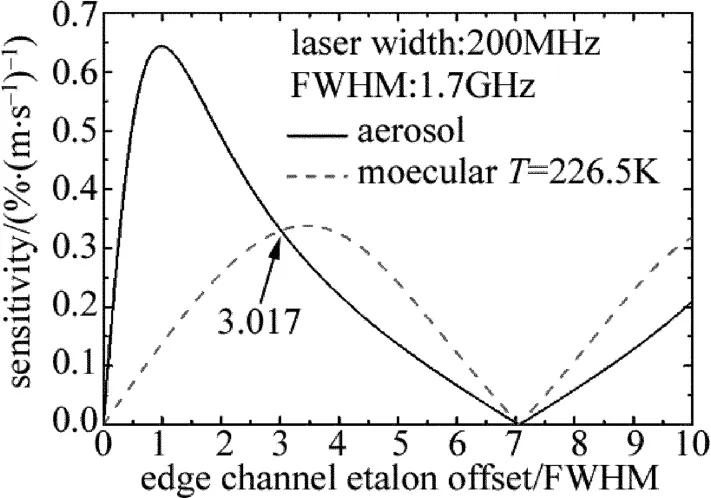
Fig.3 The velocity sensitivity for Rayleigh signal and the Mie signal as a function of the separation between two edge-channels of the etalon

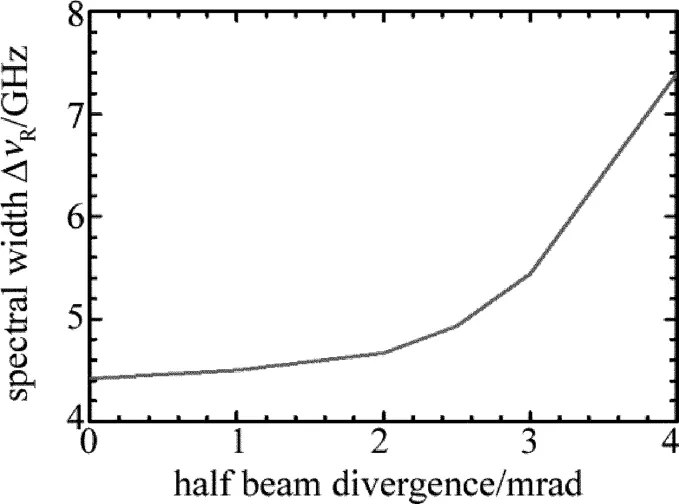
Fig.4 The etalon spectrum width for various half beam divergence angle

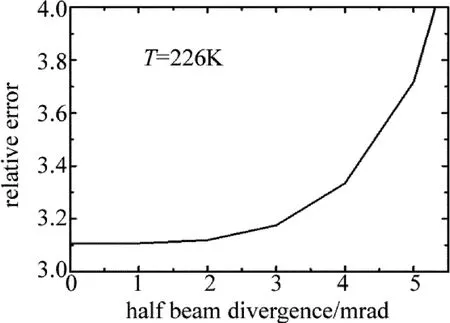
Fig.5 Relative errors for various half beam divergence angle

同样，光束发散也会对F-P标准具出射的瑞利散射产生谱线的展宽和透过率峰值的下降，图4所示是F-P标准具透过率与入射光束发散角的关系。可以看出，与气溶胶散射相比，基于瑞利散射的F-P标准具容许较大的入射光发散角。由发散角引起的相对测量误差如图5所示，当发散角为3mrad时，相对误差增大6.9%，如果选取由于光束发散引起的相对测量误差为5%以内，则可以选取光束发散角在2mrad以内。

另外，由于分子后向散射谱的宽度比气溶胶后向散射谱宽度大很多，因此要选择足够大的标准具自由谱宽度（free spectral range，FSR）xFSR以满足瑞利后向散射谱的要求，才不至于使分子后向散射信号进入标准具干涉条纹的相邻级而产生测量误差。但xFSR的取值还受光谱分辨率和条纹精细度的限制，不能太大。如果有效精细度F确定，则xFSR增大，必然导致光谱分辨率的FWHM降低，灵敏度下降；若FWHM确定，xFSR增大将导致F增大，F增大，则表面镀膜反射率R增大，这将直接导致峰值透过率的减小，最终影响信噪比，所以xFSR并非越大越好。工作波长355nm时，在10km～40km高度范围内随着温度的变化瑞利后向散射谱宽ΔνR≈1.4GHz～1.7GHz，对于瑞利高斯谱线，99.73%的瑞利信号集中在6ΔνR的频率范围内。再考虑通过上述交叉区域确定的峰值间距及径向风速测量动态范围等因素选择FSR为12GHz，以确保绝大部分瑞利信号可以被接收。选取的F-P标准具的参量见表1。

Table 1 Three-channel Fabry-Perot etalon parameters for Rayleigh Doppler wind lidar based on 355nm wavelength

3 F-P标准具透过率曲线校准

3.1透过率曲线校准分析

基于F-P标准具频率检测的双边缘技术，径向风速测量精度极大地依赖于标准具透过率曲线校准参量，主要包括：峰值透过率Tp、峰值位置νp、半峰全宽FWHM、自由谱宽xFSR和有效反射率R等。因此，测量前必须严格的对标准具透过率曲线进行校准，以提高风场测量精度。

对于F-P标准具频率检测的双边缘激光雷达系统，标准具工作在接近垂直入射时的中央条纹上，为了获得最佳性能，要求更高水平的光束准直度。由于分子信号的大谱宽，因而F-P标准具要求的光谱分辨率相对较低，且照射到标准具表面的光束发散角相对较大。如上所述光束发散角最大不超过2mrad。光束准直后经过F-P标准具的光强分布如图6所示，由图可见，标准具3个通道光强连续变化，间隔分明，左侧信号1通道先达到最亮，其次是中间的锁定通道，最后是右侧信号2通道，每个通道光强最大时基本均匀充满标准具各通道孔径，且锁定通道与信号2通道的间隔明显小于锁定通道与信号1通道的间隔，表明锁定通道峰值与信号2通道峰值靠近，与设计指标要求的锁定通道半峰全宽处位于两边缘通道对称交叉点处相吻合，用于锁定发射激光频率［12］。

Fig.6 Light intensity change passing through three channels of the etalon after the optical alignment

3.2透过率曲线扫描取样

由探测器计数率校准可知，标准具透过率曲线扫描时对光强有严格要求，使探测器计数率保持在0.1MHz～1MHz之间，以确保探测器工作在线性状态减小计数误差。光子计数探测器接收的光信号由光子计数采集卡采集并保存为原始光子数据列N1（νn）（边缘通道信号1）、N2（νn）（边缘通道信号2）和Ne（νn）（边缘通道能量），模拟探测器采集的光信号转换为电压信号由A／D采集卡采集并保存为数据列VLS（νn）（锁定信号）和VLE（νn）（锁定能量）。并利用以下公式计算透过率：

式中，Ti为边缘通道透过率，TL为锁定通道透过率，n为透过率扫描的步数，νn为扫描第n步对应的频率。

由于采用脉冲光扫描透过率，信号波动相对较大，因此扫描时采取增加脉冲累计数提高信噪比，一般情况下脉冲累计2000；另外，随着扫描过程的深入，长期工作的激光器会产生缓慢的频率漂移，而且对于种子注入式的激光器在特定温度下还会出现频率跳跃现象，为了减少激光器频率漂移或跳跃带来的影响、缩短扫描时间，调节标准具腔长100步一扫；尽管如此，扫描过程中的各种不确定因素仍然会导致不同时间扫描出的标准具透过率曲线谱存在差异，为了克服各种不确定因素带来的偶然误差，采取增加扫描次数取平均的方法。

3.3透过率曲线拟合及校准误差分析

将F-P标准具透过率函数进行级数展开，则1阶函数形式为：

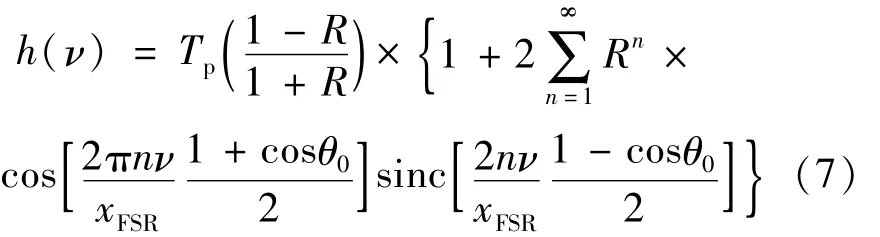
式中，Tp，xFSR分别表示峰值透过率和自有谱间距，R表示标准具表面镀膜的反射率，ν为发射激光频率，θ0为发散角。瑞利散射信号经过标准具后的透过率函数理论表达式：

对标准具扫描所得一系列离散点T1（νn），T2（νn）和TL（νn）进行最小二乘法拟合，拟合结果如图7所示。由图可见双边缘信号1通道和信号2通道峰值略有差别，可能是由于分束片分束比不同导致两通道接收光强不一致所致；锁定通道峰值相对较低，但有相对较窄的透过率曲线FWHM和相对陡峭的斜率用于激光频率锁定，因此对锁定效果没有影响。两边缘通道FWHM大于理论设计值，究其原因可能有以下几方面：（1）光束发散角没有调整到最佳状态，直接影响透过率曲线的FWHM和峰值高度；（2）标准具两平行玻璃板没有调平行，导致不同程度的腔长差使FWHM增宽和峰值降低；（3）标准具表面缺陷也有可能产生部分影响。

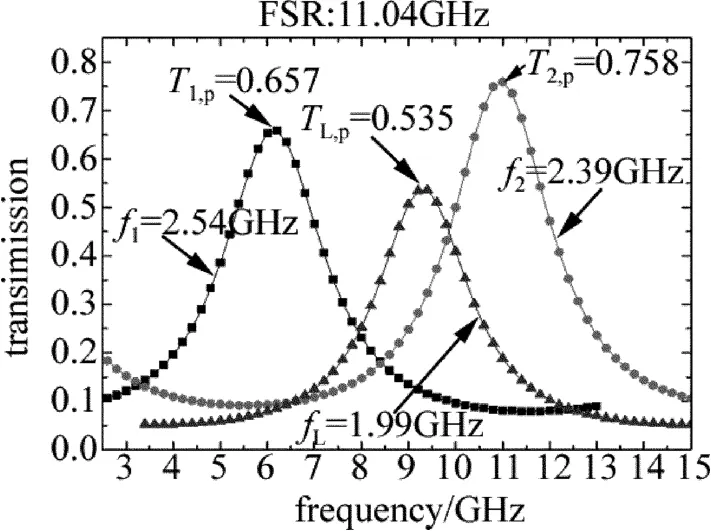
Fig.7 Calibrated parameters of the three-channel Fabry-Perot etalon

利用校准得到的透过率曲线参量，可以计算出F-P标准具透过率曲线的速度灵敏度，如图8所示。实际测得零多普勒频移时的速度灵敏度为0.527%／（m·s－1），较设计时的0.645%／（m· s－1）下降了0.118%／（m·s－1）。造成速度灵敏度下降的主要原因是实际校准得到的标准具两边缘通道频谱的FWHM增大所致。根据（4）式计算出2010-08-11T17：47测量的大气回波信号的强度分布，如图9所示。由图可见，40km高度处大气回波信号信噪比大于10。根据多普勒速度测量的误差估算（3）式，即均方误差是多普勒频率响应函数的相对灵敏度和系统探测的总信噪比的乘积的倒数关系，实际测得的系统随高度变化的径向速度估算误差分布如图10所示。由图可见，20km高度以下，径向速率测量误差不到1m／s，20km以上随着信噪比下降径向速率测量误差迅速增大，40km左右的径向速率测量误差约8m／s，与系统设计径向速速率计算精度相比增大了2m／s。系统误差的增大不仅包括标准具透过率曲线的校准误差所产生的影响，还包括实际风场测量过程中由于透过率曲线FWHM增大导致气溶胶和瑞利散射信号速度灵敏度不相等，在径向风速反演过程中使气溶胶信号成为干扰信号所产生的误差，如图11所示。由图可见，后向散射比相同时应用实际校准的透过率曲线参量获得的径向速度测量误差比理论设计值大很多倍，且误差关于零点不对称，即零多普勒频移时就产生一定误差。当然，系统误差还包括系统运行过程中器件参量变化、测量期间气候变化、电噪声、热噪声以及探测器计数差异等诸多因素的影响。

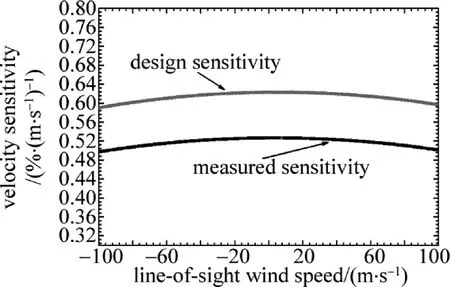
Fig.8 The designed line-of-sight velocity sensitivity compared with the calibrated it

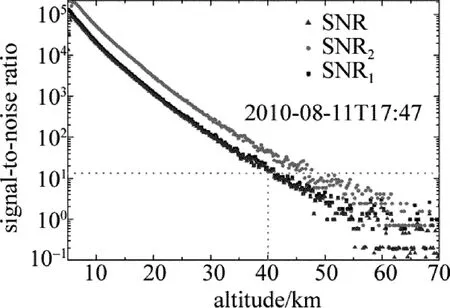
Fig.9 The signal-to-noise ratio distribution of the backscattered signal from two edge-channels of the etalon

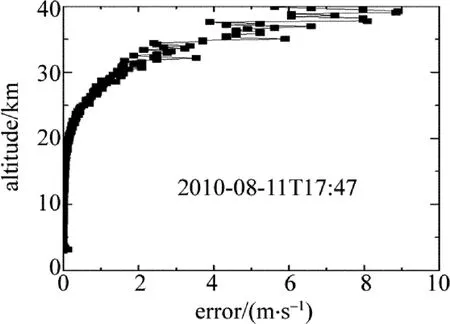
Fig.10 Line-of-sight velocity accuracy distribution measured along with altitude

Fig.11 Line-of-sight speed error as a function of Doppler frequency at different backscattering ratio Rb

4 小 结

基于F-P标准具的双边缘瑞利信号检测技术目前已成为国际上中高层大气风场测量普遍采用的手段，其核心就是F-P标准具参量的优化设计和精确校准。本文中首先介绍了利用F-P标准具检测的瑞利散射激光雷达多普勒频移测量原理，根据理论分析详细地介绍了F-P标准具透过率曲线参量的优化选取过程，提出了透过率曲线的详细校准过程及方法，分析了透过率曲线校准误差产生的原因。利用实际校准参量计算透过率曲线风速测量的速度灵敏度及系统测量误差，得出了透过率曲线校准误差对风速测量速度灵敏度和系统测量误差产生的影响。分析表明，透过率曲线的校准精度直接影响系统径向速度测量精度。

［1］ XUW J，SUND S，SHU Z F，et al.Wind velocity inversion algorithm for triple-channel Rayleigh Doppler wind lidars［J］.Laser Technology，2011，35（4）：481-485（in Chinese）.

［2］ LIC，SHU Zh F，XUW J，et al.Development of molecule wind lidar receiver based on Fabry-Perot［J］.Laser Technology，2011，35（2）：156-159（in Chinese）.

［3］ KORB C L，GENTRY BM，LISX，et al.Theory of the doubleedge technique for Doppler lidar wind measurement［J］.Applied Optics，1998，37（15）：3097-3104.

［4］ FLESIA C，KORB C L.Theory of the double-edgemolecular technique for Doppler lidar wind measurement［J］.Applied Optics，1999，38（3）：432-440.

［5］ KORB C L，GENTRY B M，WENG C Y.The edge technique：theory and application to the lidar measurement of atmospheric winds［J］.Applied Optics，1992，31（21）：4202-4213.

［6］ KORB C L，GENTRY BM，LIS X.Edge technique Doppler lidar wind measurements with high vertical resolution［J］.Applied Optics，1997，36（24）：5976-5983.

［7］ GENTRY B M，CHEN H.Tropospheric wind measurements obtained with the goddard lidar observatory for winds（GLOW）：validation and performance［J］.Proceedings of IEEE，2001，4484：74-81.

［8］ GENTRY BM，CHEN H L.Profiling tropospheric winds with the goddard lidar observatory for winds（GLOW）［C］／／Proceedings of the 21st International Laser Radar Conference.Washington，D C，USA：NASA，2002：4p.

［9］ GENTRY B M，CHEN H L，LI S X.Wind measurements with 355nm molecular Doppler lidar［J］.Optics Letters，2000，25（17）：1231-1233.

［10］ FLESIA C，KORB C L，CHRISTINA H.Double-edge molecular measurement of lidar wind profiles at355nm［J］.Optics Letters，2000，25（19）：1466-1468.

［11］ SHEN F H，CHA H，SUN D S，et al.Low tropospheric wind measurement with Mie Doppler Lidar［J］.Optical Review，2008，15（4）：204-209.

［12］ TANG L，WANG Y T，SHU Zh F，et al.Analysis of detectors and transmission curves correction of mobile rayleigh Doppler lidar［J］.Chinese Physics Letters，2010，27（11）：114207.

Design and calibration of the Fabry-Perot etalon in Rayleigh backscattering Doppler w ind lidar

TANGLei1，WUHaibin2，SUNDongsong3，SHUZhifeng3
（1.Department of Physics and Engineering，Hefei Normal University，Hefei230031，China；2.School of Physics and Material Sciences，Anhui University，Hefei230031，China；3.School of Earth and Space Sciences，University of Science and Technology of China，Hefei230031，China）

The Fabry-Perot etalon was the key component of a Rayleigh Doppler wind lidar.In order to accurately determine the Doppler shift proportional to the wind velocity，the principle of Rayleigh Doppler frequency measurement was deeply analyzed，and the optimum parameters of the etalon were determined after analyzing the detection error at the maximum height designed.The calibration method and idea were introduced in detail.The factors making the full width at half maximum（FWHM）of the transmission curves broadened were analyzed，the calibration accuracy of the transmission curve affecting the velocity sensitivity and the system measuring error was also analyzed in detail.The design and calibration were verified in experiments.The result indicated that the velocity sensitivity of etalon decreased 0.118%／（m· s－1）due to the broadened FWHM of transmission curves and with the signal-to-noise ratio no less than 10，the accuracy of the line-of-sight velocity increased 2m／s at40km altitude height.

laser technique；lidar；Fabry-Perot etalon；Rayleigh backscattering；Doppler frequency

TN958.98

A

10.7510／jgjs.issn.1001-3806.2014.02.029

1001-3806（2014）02-0283-06

安徽省高校省级自然科学研究重点资助项目（KJ2013A223）；地球空间环境与大地测量教育部重点实验室开放基金资助项目（L08-3）

唐 磊（1972-），男，讲师，主要从事激光遥感信息控制与处理方面的研究。

*通讯联系人。E-mail：whb62＠163.net

2013-04-18；

2013-07-17