铝材管道管壁厚度对激光超声信号影响的探究

王贵鑫，严 刚，关建飞

铝材管道管壁厚度对激光超声信号影响的探究

王贵鑫，严 刚*，关建飞

（南京邮电大学光电工程学院，南京210023）

为了探究管壁厚度对超声信号的产生与探测的影响，采用有限元法建立了理想化的管道模型，分别探究均匀管壁厚度变化和激发源处、接收端处及传播路径上等畸变管壁厚度的变化对超声信号产生的影响。结果表明，当接收端处管壁厚度较薄时，无法探测到可分辨的瑞利波信号；传播路径上管壁厚度变小到一定程度后，高频成分会出现明显的衰减，但随着厚度的增大又会在一定程度内恢复。这一结果对激光超声在柱状、管状材料的无损检测中的进一步应用提供了有益的补充。

激光技术；激光超声；有限元法；无损检测

引 言

管道在制造、储藏运输、焊接及长期的使用过程中，不可避免地会形成锈迹、焊渣、防锈剂、泥沙等杂质的沉积，对于一些永久性的设施，如供水管道、输油管道、输气管道等，经过长期的使用甚至还可能出现比较严重的腐蚀，因此对于管道的检测就显得十分重要。参考文献［1］～参考文献［3］中对柱状材料进行了相关的数值模拟，并采用双积分变换法计算了激光在圆柱体中激发的柱面表面波波形。参考文献［4］中给出了有限元中网格大小的划分，对时间步长的选取作了科学的论证。DONG等人［5］提出了基于光热调制的激光声表面波检测疲劳裂纹的实验系统和方法，并将其用于发动机叶片疲劳裂纹的检测。FENG等人［6］分析了超声位移场随时间变化的特征。LIU等人［7］采用有限元法模拟了铝状板材中声表面波的激发过程，为改善激光超声检测中声表面波的信噪比提供了一定的理论依据。

近年来，研究人员致力于将激光超声技术应用于管道材料的相关研究，这使得管道材料中激光超声的激发、传播及缺陷对超声信号的调制等问题成了急需解决的热点问题。CAO等人［8］采用环状激光源研究了铝管内部温度分布。参考文献［9］中采用激光超声技术检测了铁及铝圆柱表面的裂缝，讨论了圆柱表面激光瑞利波与缺陷的相互作用。ZHAO和HE等人［10-11］研究了柱状和管状材料中超声波的激光激励及其传播的有限元模型及算法，从理论及实验方面研究了柱状和管状材料中激光激励超声波的传播特性，及其在复杂结构材料的无损检测领域的应用。然而目前的研究大多集中于规则管道，而对于生活中由于腐蚀等因素引起的不规则管道的相关研究则鲜见于报道。因此，本文中结合有限元法的优势，研究薄管及不规则管道中瑞利波的激光激发和传播过程。

作者主要对一些特殊情况的管道进行理想化的模拟处理，以期找到一些通用的规律，为管道超声无损检测提供必要的支持。

1 铝质偏心管道有限元模型

本文中在对均匀管道探究的基础上，建立非均匀管道的理想化模型，对实际情况进行简化处理。具体模型如图1所示，其中图1a是均匀管道模型，图1b～图1d分别是3种不同的非均匀模型。图1b对应的激发源处厚度适中，但是在超声信号的传播路径上出现了厚度的畸变，主要是为了探究传播路径上管壁厚度的畸变对超声信号的影响；图1c对应的是激发源管壁厚度比较薄的情况，主要是为了探究激发源管壁厚度的变化对超声信号的相应影响；图1d对应的是探测角处比较薄的情况，主要是为了探究在管壁畸变处探测超声信号时可能受到的影响。作者在对图1a和图1c对应模型的分析基础上，重点对图1b和图1d对应的模型进行了探究分析。α表示信号探测角，其中x轴处表示0°探测角，R2表示管道外径，R1表示管道内径。

Fig.1 The excitationmodel of uniform and non-uniform cylinder（detection angleα）

在本文中的3个非均匀模型中，考虑到结果的精度及运算时间的双重因素，将模型分为两个部分，采取不同的网格划分密度，即在激光直接作用区域采用高密度的网格，在激光不能直接作用的区域采用较低密度的网格。当模型外径为10mm时，1°的圆心角对应的弧长约为174μm，同时考虑到采用的激光线源的半宽为100μm，为保证加密区充分涵盖热作用区，故对探测角度数在－2°～2°的扇形区域内采用细网格，单元边长选为20μm，在模型的其它区域采用较粗网格，单元边长选为40μm。

2 缺陷管道中超声波的传播规律分析

考虑到模型的可对比性，首先分别对图1a～图1d进行对比分析，即以图1a为参照模型，在此基础上将模型中的内圆沿x轴正方向偏离一定单位形成模型（见图1c），将模型中的内圆沿x轴负方向偏离一定单位形成模型1（见图1d），这种情形下的图1a、图1c和图1d为一组对比模型。由于对图中每个模型都有一系列的数值模拟分析，为了便于区分和对比，对具体的模型采用如下两种命名方式：（1）α（R1，R2），这是对均匀管道模型的命名；（2）α（ecXmmβ（R1，R2）），这是对偏心管道的命名规则，其中α表示信号探测角，ec表示是偏心模型，X表示偏心位移量（单位是mm），β表示偏心方向（取值分别为0°，90°和180°，分别表示沿x轴正方向、y轴正方向、x轴负方向偏移）。

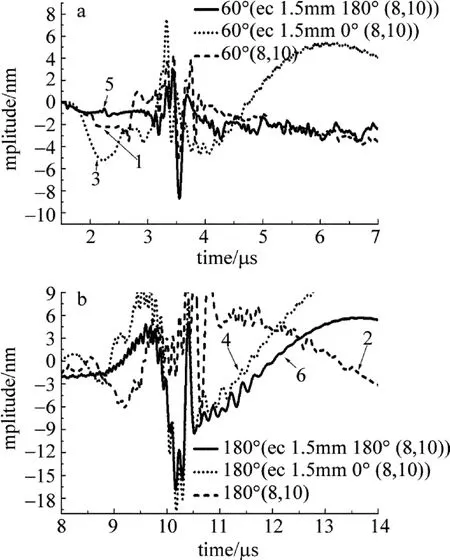
Fig.2 The ultrasonic signal of the uniform and non-uniform model（60°，180°，R2＝10mm，R1＝8mm）

图2是分别对应如图1a、图1c和图1d 3种模型在60°和180°探测角处探测到的对比波形。图2a中的曲线1和图2b中的曲线2对应的模型是内径为8mm、外径为10mm的正常圆管。图2a中的曲线3和图2b中的曲线4是在图2a中的曲线1对应模型的基础上，将内圆沿x轴正方向偏离1.5mm后得到的模型，这种模型下，激发源中心处的厚度为0.5mm（厚度＝壁厚－偏移量）。而图2a中的曲线5和图2b中的曲线6则是将内圆沿x轴负方向偏离1.5mm后得到的模型，这种模型下激发源处的厚度为3.5mm（厚度＝壁厚＋偏移量）。图3是分别与图2对应的频谱分析图。从图2a中的曲线1、曲线3、曲线5和图2b中的曲线2、曲线4、曲线6可以看出，在同一探测角处探测到的波形也表现出比较大的差异。从超声波形上看，图2a中的曲线1、曲线5上表现出明显的瑞利波信号，图2a中的曲线3则表现出兰姆波的特征，而图3中相应的频谱图也反映出了这一点。从管壁厚度来看，图2a中的曲线1、曲线5从激发源到60°探测角的区域的厚度均大于等于2mm，而且图2a中的曲线5的局部厚度甚至达到3.5mm，它所表现出的超声信号也与在相同厚度的圆管中同探测角下测得的信号一致。从图2b中的曲线4、曲线6可以看出，在两种偏心模式下，对心处接收到波形似乎是一致的，但是从图3b中的曲线4、曲线6可以看出两者之间明显的差异，图2b中的曲线4其高频信号明显增多，而且成分更加复杂。两种偏心模型下的波形与正常圆管中测得的波形也是不同的，主要表现是出现兰姆波的特征和极性的反转。

图3a中曲线1低频部分的几个峰值分别为0.333MHz，1.33MHz，2.33MHz和2.66MHz；曲线3低频部分的几个峰值分别为0.286MHz，0.573MHz，0.860MHz和1.147MHz。从这几组数据可以看出，超声信号的频率明显下降，而且相对比较集中，从图3a中可以看出，曲线3的高频部分几乎消失。这说明较薄的管壁能够影响高频信号的产生。图3a中曲线5低频部分的几个峰值为1.31MHz，1.75MHz，2.19MHz和2.63MHz。这是在激发源较厚处得到的信号频率，与之前的两组数据对比可以看出，频率值明显比曲线3中的要高，而与曲线1相比也有所区别，但幅值范围基本一致。

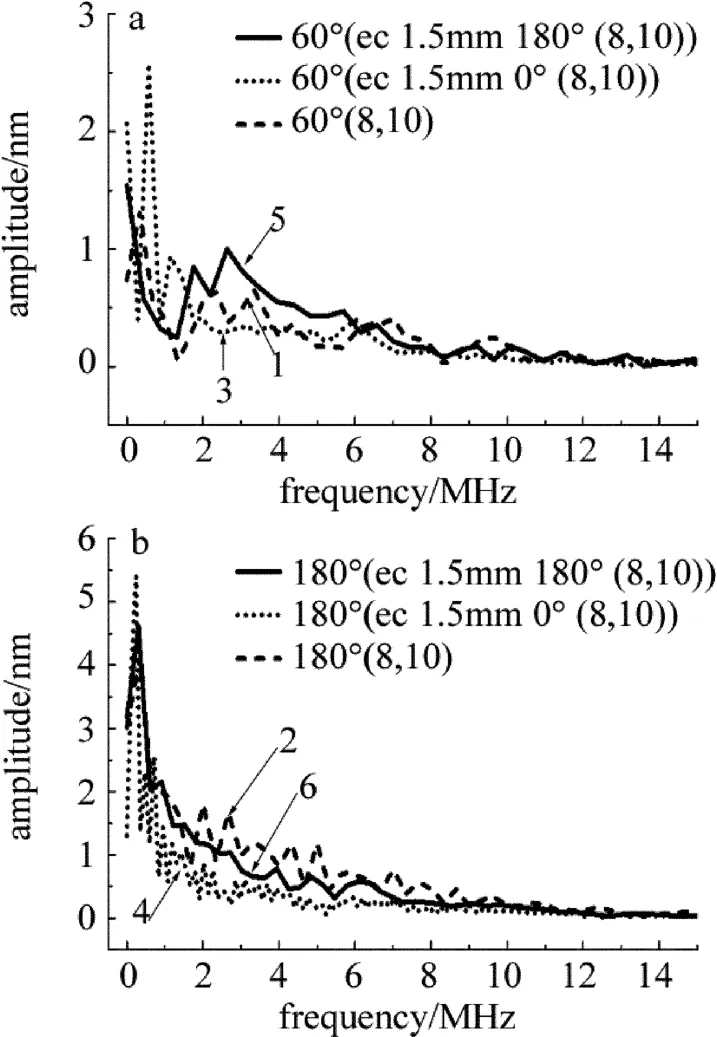
Fig.3 The spectrum of the ultrasonic signal of the uniform and non-uniform model（60°，180°，R2＝10mm，R1＝8mm）

图3b中曲线2的最小几个峰值分别为0.333MHz，1.667MHz，2.001MHz和2.335MHz，而曲线4最小的几个峰值分别为0.238MHz，0.357MHz，0.476MHz，0.595MHz，0.714MHz，0.833MHz，0.952MHz和1.071MHz。图3b中曲线4对应的模型是在薄处激发、厚处接收的，但从频率上来看，超声信号的频率并没有恢复到正常值，这就是说激发源对超声信号的影响是不可逆的。曲线6得到的频率值与曲线2得到的值相比只有微小的差别，这说明当激发源处的厚度满足一定条件时，接收端处的畸变只是对信号的幅度有一定的影响，而基本不会改变信号的频率，即不会影响信号的成分。

在实际的检测中，也存在这样一种情况，即在超声信号的传播路径上也可能会遇到管壁畸变的情况，而这些畸变信息也很可能会对传播中的超声信号起到某种调制作用。针对这种情况，特建立如图1b所示的原始模型，并以该模型为基础，进行了几组有限元仿真模拟。

图4所对应模型的内径为8mm，偏心幅度为1.5mm，这样畸变管道最薄处只有0.5mm。为了能够更加清晰地研究管壁畸变（由厚变薄）对超声信号传播的影响，从激发源处，分别沿顺时针和逆时针两个方向在对称位置处探测超声信号。图4a中的曲线1、曲线2是在探测角分别为30°和330°处探测到的波形信号，从图中可以看出：瑞利波信号的幅度及到达的时间基本一致，这说明两个探测点到激发源的距离是相同的；而30°探测角处的超声信号中，在瑞利波之后出现了很多小的峰值，而在330°处探测到的超声信号中的则没有相应的峰值，这些峰值很显然是由管壁厚度的变化（变薄）引起的，其具体的成因则需要进一步地模拟探究分析。从图4b中的曲线3可以看到一个很小的与曲线4中瑞利波信号极性相反的信号，从到达时间上来说，这个较弱的信号到达得要早一些，即速率要比曲线4中的要快一些。从图4c中的曲线5和曲线6显示的第1组波形信号（约出现在8.5μs处）来看：经过畸变管壁调制后的信号到达时间要早一些，即波速要快一些；而且就幅度而言，已与从较厚一侧传过来的信号相当，这说明在这种模式下，畸变信号有一定的恢复能力；未经畸变管壁调制的信号（见曲线6）仍然表现出强烈的色散现象，而经畸变管壁传播而来的信号则没有明显的色散，而其具体的成分则有待于进一步的频谱分析。

Fig.4 The ultrasonic waves of the eccentricmodel（offset1.5mm along the positive y-axis direction，R2＝10mm，R1＝8mm）

图5是与图4所对应的频谱图，图5b中的曲线3、曲线4是在与激发源等距离的对称位置处探测到的信号的频谱分析图，同样可以看出，较薄管壁对超声信号高频部分有明显的吸收作用。图6为沿y轴正方向偏离1.1mm时的波形分析图，图7是与图6对应的频谱分析图。图7b中的曲线3、曲线4与图5b中的曲线3、曲线4相同，都可以看到类似的情形。图5a中的曲线1、曲线2与图7a中的曲线1、曲线2都是对激发源附近探测到的信号的频谱分析，可以看出较厚的一侧（330°探测角处）比较薄一侧信号的高频部分要强一些。图5c中的曲线5、曲线6与图7c中的曲线5、曲线6都是对经过畸变管壁调制后的信号所做的频谱分析，可以看出两者的差别并不明显，也就是说超声信号穿过畸变管壁后得到了一定的恢复，也可以说畸变管壁对超声信号的影响是可逆的。

Fig.5 The spectrum of the ultrasonic signal of the eccentricmodel（offset1.5mm along the positive y-axis direction，R2＝10mm，R1＝8mm）

图6对应的模型与图4对应的模型相比，唯一的区别就是偏移量有所不同，本模型中偏移量为1.1mm，这样管壁最薄处只有0.9mm。选择这样一组偏移量是因为在之前的研究中发现瑞利波约在管壁厚度为0.9mm时出现突变。而将图6中波形信号与图4中相应的波形信号相比，确实表现出一定的差异性。首先对比沿顺时针方向传播的波形（见图4和图6中的曲线2、曲线4、曲线6，其都是从较厚的管壁一侧传播的），无论从到达时间还是振幅都无明显不同，甚至色散部分都有一定的一致性。而再对比沿逆时针方向传播的信号，则可以发现明显的差异，即图6对应的模型的偏移量比较小，但是产生的影响却更大：图6b中的曲线3的低频信号明显比图4中的低频信号强，甚至已经淹没瑞利波信号（图中约出现在5.3μs处）；图6c中曲线6与图4c中曲线6相比，经畸变管道调制的信号只是在部分上恢复，从信号强度来说，要弱得多。

Fig.6 The ultrasonic waves of the eccentricmodel（offset1.1mm along the positive y-axis direction，R2＝10mm，R1＝8mm）

对比图7和图5可以发现，两者表现出极大的相似性：在两种偏心厚度下，在90°探测角处都出现了较大的信号衰减，即同样是高频部分消失；但在150°探测角处探测到信号中又表现出一定程度的恢复，这一点从波形图（见图4和图6）上可以更清晰地看到。

从图4和图5、图6和图7两组图中都可以看到，畸变管壁有一定的滤波作用，经过畸变管壁的超声信号的频率较高的部分有比较大的损失，在图中的表现就是只有一个强的低频信号，而且这种现象从图4中相应的部分也可以清楚地看到。

Fig.7 The spectrum of the ultrasonic signal of the eccentricmodel（offset1.1mm along positive the y-axis direction，R2＝10mm，R1＝8mm）

3 结 论

建立了3种典型的渐变缺陷管道有限元模型，探究激发源处、接收端处和传播路径上一定范围内渐变管壁对超声信号产生及传播的影响。其中，第1种渐变管道有限元模型（见图1c）是为了探究激光源处管壁厚度的变化对超声信号的产生与传播的影响，第2种渐变管道模型（见图1d）是为了探究接收端处管壁厚度变化对接收的超声信号的影响，第3种渐变管道模型（见图1b）则是为了探究超声信号经过畸变管壁调制后可能存在的影响。

分析结果表明，在这种渐变模型下，激发源处管壁厚度的变化对超声信号的产生有着特殊的影响，主要体现在：接收端处管壁厚度小于1mm时，接收到的信号（激发源处厚度大于2mm）会出现极性的翻转，较高频率的部分会被吸收，特别是当接收端管壁厚度为0.9mm或小于0.5mm时，绝大部分的信号都会被吸收掉；激发源处和接收端处的管壁厚度都大于2mm时，而在超声信号的传播路径上管壁较薄（小于1mm）时，接收到信号与激发源处的信号相比，主信号没有明显的不同，但主信号附近的高频成分会损失，体现在波形上就是主信号附近的色散有所减弱。

［1］ WU X，QIAN M，CANTRELL JH.Dispersive properties of cylindrical Rayleigh waves［J］.Applied Physics Letters，2003，83（19）：4053-4055.

［2］ HU W，QIAN M，CANTRELL JH.Thermoelastic generation of cylindrical rayleigh waves and whispering gallerymodes by pulsedlaser exeitation［J］.Applied Physics Letters，2004，85（18）：4031-4033.

［3］ PAN Y，ROSSIGNOL C，AUDOIN B.Acoustic waves generated by a laser line pulse in a transversely isotropic cylinder［J］.Applied Physics Letters，2003，82（24）：4379-4381.

［4］ FRANK S，BERND K，ALEXANDER P.Time domain modeling of axisymmetric wave propagation in isotropic elastic media with CEFIT-cylindrical elastodynamic finite integration technique［J］.Journal of Computational Acoustics，2001，9（3）：1127-1146.

［5］ DONG LM，LIJ，NICh，et al.Crack detection of engine blade based on laser-heating assisted surface acoustic waves generated by scanning laser［J］.Chinese Journal of Lasers，2011，38（11）：84-88（in Chinese）.

［6］ FENGW，YANGD X，LIAOW，etal.Numerical simulation of laser induced ultrasonic in a diamond anvil cell by finite element method［J］.Chinese Journal of Lasers，2011，38（8）：89-94（in Chinese）.

［7］ LIU JSh，XU Zh H，GU GQ.Numerical study on improvementof signal-to-noise ratio of surface acoustic waves based on laser array［J］.Laser Technology，2011，35（3）：403-406（in Chinese）.

［8］ CAO D D，WANG K Sh，YANG Y Y.Fintite element simulation of temperature field of thin tubes irradiated by ring lasers［J］.Laser Technology，2010，34（6）：753-756（in Chinese）.

［9］ CLORENNECD，ROYER D，CATEELINE S.Saw propagating on cylindrical parts using laser-ultrasonics：application to crack defection［J］.IEEE Ultrasonics Symposium，2002，1（8／11）：207-210.

［10］ ZHAO Y.Theoretical and experimentalstudy of the laser-induced ultrasonic waves at fluid-solid interface and curved surface［D］.Nanjing：Nanjing University of Science and Technology，2007：5-19（in Chinese）.

［11］ HE Y J，ZHU R H，SHEN Zh H，et al.Simulation of laser-induced temperature fields and rayleigh waves in thick Al pipe［J］.Journal of Nanjing University of Science and Technology，2005，29（4）：468-471（in Chinese）.

Effect of wall thickness of alum inum pipes on laser-induced ultrasonic waves

WANGGuixin，YANGang，GUANJianfei
（College of Electronic Engineering，Nanjing University of Posts and Telecommunications，Nanjing 210023，China）

In order to explore effect of wall thickness on the generation and detection of ultrasound signal，several idealized eccentric pipe models were established based on the finite element method.Effect of different uniform wallthickness and thickness change at the excitation source，detection point and the propagation path on ultrasonic signal was analyzed.The simulation results show that：when the wall is thinner，the Rayleigh waves cannot be detected；the wall thickness on the propagation path becomes small to some extent，the filtering effect will be so obvious that the highfrequency component is filtered out，butwill resume within a certain extent in the pipes with thicker wall.This work will provide a useful guidance for the further application of laser ultrasonic in cylinder nondestructive testing field.

laser technique；laser ultrasonic；finite elementmethod；nondestructive testing

TN249；O426.2

A

10.7510／jgjs.issn.1001-3806.2014.02.024

1001-3806（2014）02-0260-06

王贵鑫（1986-），男，硕士研究生，主要从事激光超声的数值模拟研究。

*通讯联系人。E-mail：yang＠njupt.edu.cn

2013-03-18；

2013-06-05