弹光调制偏振Stokes参量测量及误差分析

王立福，王志斌，2*，李 晓，2，陈友华，张 瑞，张鹏飞

弹光调制偏振Stokes参量测量及误差分析

王立福1，王志斌1，2*，李 晓1，2，陈友华1，张 瑞1，张鹏飞1

（1.中北大学山西省光电信息与仪器工程技术研究中心，太原030051；2.中北大学仪器科学与动态测试教育部重点实验室，太原030051）

为了更简便地实现Stokes矢量测量，采用一种工作在不同频率上的双弹光调制器，利用它的频率叠加对光进行调制，产生载有被测量的高频调制分量，通过锁相一次得到了适用于所有偏振态测量的4个Stokes分量，且进行了理论分析、仿真验证以及误差分析，即对相位延迟幅度、入射角等因素对测量结果的影响进行了分析。结果表明，该方法实现了只需测量一次便可测出偏振态的所有分量，为进一步工程实现提供了基本的理论支撑。

光谱学；双弹光调制器；Stokes矢量；偏振；锁相

引 言

斯托克斯参量已经被广泛应用于矢量光束的偏振特性变化的研究，且可描述光束所有的偏振态和光强度，因此只要测量出全部的斯托克斯参量，即可确定不同光束的偏振态。测量斯托克斯参量的方法分为两类：一类是分振幅法［1-2］，用4个光电探测器同一时刻探测分成4束的待测光，完成对各个斯托克斯参量的测量；另一类是偏振光调制法，即在调制光路中加入相位延迟器和起偏器，只要使得它们绕光轴作多角度的转动［3］，不同角度调制结果不同，可以满足大部分偏振光的测量。目前，应用这一原理研制新型偏振测量仪已引起业内同行的密切关注，但其存在转动机械误差。近年来，随着现代偏振测量技术的快速发展，偏振调制技术也有了长足的进展。

弹光调制器就是一种运行在谐振频率状态下的偏振调制器件，弹光调制器（photoelastic modulator，PEM）是一种基于光学双折射晶体材料弹光效应的相位调制器件，自从弹光调制器发明以来，由于具有无机械振动影响、入射角较大、调制频率高且装置稳定性高、损耗小、容易控制、波段范围宽（可从真空紫外到远红外）等一系列优点［4-5］，基于上述的这些优点，这种优越的偏振调制器很快应用到了许多领域，且对光学、生物物理、物理化学、晶体生长等领域都产生了积极的推动作用。而传统的弹光调制偏振测量的方法是基于弹光调制的低频测量［6-8］，不适用于高速运动物体的光谱测量，虽然容易探测，但不适用于高速运动物体的光谱测量，并且传统的弹光调制偏振测量方法只能一次测量Stokes矢量中2个参量或者3个参量，也有可以测量出4个参量的，但是需要转动装置，降低了装置的稳定性，因此，针对传统方法的诸多不足，本文中提出了使用双弹光调制测偏振的新方法，该方法只需测量一次就可以测出Stokes矢量的4个参量，适用于所有的偏振态测量，结合光谱测量及图像融合技术可以用于高速运动物体的偏振光谱测量，且无需转动实验装置，提高了结构的稳定性，很好地弥补了现有偏振光谱测量的不足。

1 弹光调制Stokes矢量测量结构及原理

1.1Stokes矢量

偏振测量中偏振态的描述方法有4种：三角函数表示法、Jonse矢量表示法、Stokes矢量和邦加球表示法。而Stokes矢量是英国物理学家STOKES在1852年研究部分偏振光时首次提出的。由于Stokes矢量既可以描述完全偏振光，也可以描述部分偏振光和非偏振光，可以是单色光也可以是复色光，所以在所有描述光偏振特性的方法中，Stokes矢量被广泛应用。Stokes矢量可用4个参量表示所有光的偏振状态，具体表示如下［4，9-10］：

式中，和表示电场在x和y方向的振幅，〈〉表示对时间的平均值，φ1＝φx－φy表示x方向和y方向上相位差，φ2＝φy－φx表示y方向和x方向上相位差，S0表示光的总强度，S1表示光的x分量和y分量的强度差，S2表示光在＋45°或－45°方向线偏振分量的强度差，S3表示光的右旋圆偏振分量与左旋圆偏振分量的强度差。

对于全偏振光有［9］：，部分偏振光有，自然界中的光包含的圆偏振信息很少，而一般的偏振测量装置测量的偏振信息主要是对Stokes矢量中S0，S1和S2的测量，为此对S3的测量变得尤为重要了。基于几种偏振态的的类型，本文中提出了一种使用双弹光调制器测偏振态的新方法，该方法只需一次测量就可以测出Stokes的4个参量，适用于任何偏振态的测量。

1.2测量原理及结构

光通过弹光调制器后的相位延迟为［4］：

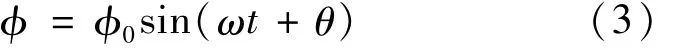
式中，ω为调制器的频率，θ为初相位，相位延迟的幅值为：

式中，d为弹光晶体通光方向的厚度，λ为光波波长，K是与弹光晶体和压电晶体有关的系数，V0为对应驱动电路的电压峰值［11］。

弹光调制偏振测量结构如图1所示，由1组2个弹光调制器（PEM1，PEM2）＋1个检偏器（P）组成，以PEM1的光轴建立为实验室坐标系，其中PEM1与PEM2的相位延迟方向分别为0°与45°，P的检偏方向为0°。

Fig.1 Stokes vectormeasurement schematics based on dual-photoelastic modulator

由弹光调制器的概念可知，当一束光通过该装置时，PEM1和PEM2产生调制，相当于可变波片，所以，通过该装置最终得到的Stokes矢量为［4，9］：

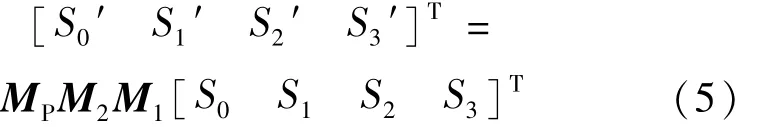
式中，矢量［S0S1S2S3］T为被测光的Stokes矢量，［S0′S1′S2′S3′］T为经过调制和检偏器之后的Stokes矢量，矩阵M1，M2，MP分别为PEM1，PEM2和检偏器P的Mueller矩阵［12］，表示如下：

式中，φi＝φ0isin（ωit），其中i＝1，2。

这样，弹光偏振测量结构的系统Mueller传输矩阵为［11-13］：

而探测器只能接收总的光强S0′，可以得到接收到的总光强为M矩阵的第1行与入射光Stokes量的乘积：

将cosφi和sinφi用贝塞尔函数展开得［14］：

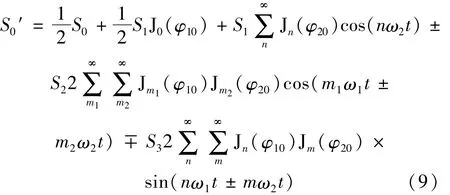
式中，m为奇数，n为偶数，Jx（y）是对应y下的第x级贝塞尔函数，m1和m2为两个弹光调制器相位延迟贝塞尔函数展开后的级数，ω1和ω2分别为两个弹光调制器的工作频率。由（9）式可知，在探测器探测到的光强中只要测得直流分量、高频频频率2ω2和（ω1＋ω2）以及（2ω1＋ω2）分量以获得S0，S1，S2和S3，因此通过锁相技术，以光弹调制器的驱动信号作为参考信号，从探测器的输出信号中解析高频频分量就可以求得S1，S2和S3，由（9）式可得直流分量、高频频率为2ω2和（ω1＋ω2）以及（2ω1＋ω2）分量随时间的变化分别为：

式中，SDC′表示探测信号直流分量，J2（φ20）≠0，J1（φ10）J1（φ20）≠0和J2（φ12）×J1（φ20）≠0，则可求得S0，S1，S2和S3如下式所示：

式中，A，B，C分别表示探测信号频率为2ω2，（ω1＋ω2）和（2ω1＋ω2）分量的幅值。由上述推导可知，在一次测量中，只需得到探测光电流的频率分量（0，2ω2，ω1＋ω2，2ω1＋ω2），就可以实现对被测光斯托克斯矢量中S0，S1，S2和S3的测量。

2 仿真结果与误差分析

2.1仿真分析

为了验证上述理论的一般性，使用MATLAB软件仿真时，偏振光被选为部分偏振光，设被测光S0＝1.00，S1＝0.60，S2＝0.30，S3＝0.50，两驱动频率分别是f1＝50.00kHz和f2＝30.00kHz，其中ωi＝2πfi（其中i＝1，2），相位延迟幅值φ10＝2.5rad，φ20＝2.0rad，带入（8）式得到结果如图2a所示，这是被测光通过双光弹和检偏器后的实际光强。如果对图2a中曲线锁相，测得频率为2ω2的分量S2ω2′如图2b中的实线所示，同样锁相（ω1＋ω2）和（2ω1＋ω2）的分量Sω1＋ω2′和S2ω1＋ω2′如图2b中的虚线和加圆线所示，从仿真结果图能明显看出信号的包络与周期性。

Fig.2 a—the total light intensitymeasured by the apparatus b—light intensity curve of each component

由φ10＝2.5rad和φ20＝2.0rad可得：J0（φ10）＝－0.048，J1（φ10）＝0.497，J1（φ20）＝0.577，J2（φ10）＝0.446。对仿真图（见图2a）提取直流分量SDC′＝0.487，由仿真结果（见图2b）可得光强幅值S2ω2′＝0.353，Sω1＋ω2′＝0.172，S2ω1＋ω2′＝0.257，带入（11）式可得：S0＝1.00，S1＝0.60，S2＝0.30，S3＝0.50。

2.2误差分析

相位延迟幅值φ10和φ20的大小对最终结果影响也很大。由（10）式可知，如果J2（φ20）＝0，J1（φ10）× J1（φ20）＝0或J2（φ10）J1（φ20）＝0时，探测器将测不到频率2ω2，（ω1＋ω2）或（2ω1＋ω2）的分量，所以也就得不到S1，S2或S3，并且由（10）式可以看出，J2（φ20），J1（φ10）J1（φ20）或J2（φ10）J1（φ20）越大，探测器的信号中包含S2ω2′，Sω1＋ω2′和S2ω1＋ω2′的幅值就越强，J2（φ20），J1（φ10）J1（φ20）或J2（φ10）J1（φ20）随φ10和φ20的变化如图3所示，由图3可知，J0（φ10），J2（φ20），J1（φ10）× J1（φ20）或J2（φ12）J1（φ20）最大时的φ10并不相同，所以要根据实际需要合理选择相位延迟幅值φ10和φ20，由（3）式可知，相位延迟幅值可通过驱动电压峰值来调节。

相位延迟幅值的微小偏差对求解S0，S1，S2和S3也有一定的影响，由（11）式可以得到相位延迟幅值φ10，φ20的微小变化Δφ10，Δφ20对求解S0，S1，S2和S3的偏差见下式：

Fig.3 a—J0（φ10）versusφ10andφ20 b—J2（φ20）versusφ10andφ20 c—J1（φ10）J1（φ20）versusφ10andφ20 d—J2（φ10）J1（φ20）versusφ10andφ20

造成相位延迟幅值的变化的因素有很多，如入射角的变化、驱动电压的变化等。弹光调制有通光孔径大［14］和视场角大的优点，但入射角的微小的变化也会对测量结果产生影响，入射角的变化最终会造成相位延迟幅值的变化，这种相位延迟的变化主要有两个方面的原因［15］：一是由于入射角不等于0时，在通光的路径上受到的应力不同所造成的；二是由于入射角的变化会使（4）式中d的变化，变化后的d′＝d／cosθ′（θ′为光通过光弹晶体的折射角，它满足折射定律）。在入射角很小的情况下，第1种原因影响很小，可以忽略，主要是第2种原因。接下来分析由于入射角的微小偏差对上述仿真结果造成的误差，假设光弹材料为熔融石英，结合d′＝d／cosθ′与（12）式可得到S0，S1，S2和S3的偏差，如图4所示。

Fig.4 Error in S0，S1，S2and S3resulting from tilted angles

由图4可以看出，在入射角是±10°时，求解出的S0的偏差ΔS0＝0.0034，也就是对最终S0的误差为ΔS0／S0＝0.00868／1＝0.87%；同理可得S1的误差ΔS1／S1＝0.00887／0.6＝1.5%，S2的误差ΔS2／S2＝0.00319／0.3＝1.1%，ΔS3／S3＝0.00477／0.5＝0.95%，由图4可知，随着偏移角度的变小，误差越来越小。

3 结 论

通过以上的讨论和仿真可知，采用双弹光调制测量托克斯参量方法，只需对探测信号的相应频率进行锁相，便可以一次测量同时获得斯托克斯矢量的4个分量，适用于所有的偏振光的测量，既不需要转动装置多次测量，也不需要多组装置，就可以获得高频分量。通过对信号调制幅度与相位延迟幅度关系仿真分析，对相位延迟幅值偏差对测量结果造成的误差进行分析，根据实际入射角允许的范围内选择合适相位延迟幅值，为该方法的进一步工程实现提供了基本的理论支撑。

［1］ AZZAM R M A.Division-of amplitude photopolarimeter（DOAP）for the simultaneousmeasurement of all four Stokes parameters of light［J］.Journal of Modern Optics，1982，29（5）：685-689.

［2］ CHENGM X，HE Zh J，HUANG ZH.Polarimeter system of stokes parameters based on division-of-amplitude［J］.Opto-Electronic Engineering，2008，35（5）：93-97（in chinese）.

［3］ XU C J，ZHAO JS，CAIY，et al.Several schemes of infrared polarization imaging［J］.Infrared Technology，2009，31（5）：262-266（in Chinese）.

［4］ ZHIY J，SU G Y，LIG H.A new method for calibration of photoelasticmodulator［J］.Acta Photonica Sinica，2001，30（1）：81-84（in Chinese）.

［5］ JING N，WANG Zh B，ZHANG JL，etal.Fast spectrum recovery of nonlinear optical path difference interferogram in photoelastic modulator［J］.Laser Technology，2012，36（2）：271-274（in Chinese）.

［6］ WANG B L，LEADBETTER A，ROCKWELL R R.Evaluation of a dual PEM Stokes polarimeter using different signal processing methods［J］.Proceedings of SPIE，2005，5888：251-258.

［7］ GUANW，COOK P J，JONESG A，et al.Experimental determination of the Stokes parameters using a dual photoelastic modulator system［J］.Applied Optics，2010，49（14）：2644-2652.

［8］ GUAN W，JONES G A，LIU Y，et al.The measurement of the Stokes parameters：a generalized methodology using a dual photoelasticmodulator system［J］.American Institute of Physics，2008，103（4）：043104.

［9］ LIAO Y B.Polarization optics［M］.Beijing：Science Press，2003：43-62（in Chinese）.

［10］ ZHUQCh，CHEN Sh Sh.Matrix optics introduction［M］.Shanghai：Shanghai Science and Technology Literature Press，1991：187-199（in Chinese）.

［11］ SONG Zh P，HONG J，QIAO Y L.Study on the measurement principle of Stokes elements spectral based on intensity modulation［J］.Chinese Journal of Quantum Electronics，2009，26（3）：268-271（in Chinese）.

［12］ SONG Zh P，HONG J，QIAO Y L.System design of intensity moduIation spectropolarimeter［J］.Optics and Precision Engineering，2011，18（11）：2325-2331（in Chinese）.

［13］ CHENW B，GU P F.Using Stokes vector express polarized light and application［J］.Optical Instruments，2004，26（2）：42-46（in Chinese）.

［14］ WANG Zh X，GUO D R.Introduction to special function［M］.Beijing：Peking University Press，2000：337-417（in Chinese）.

［15］ WANG B L，LIST J.Basic optical properties of the photoelastic modulator：partⅠ.Useful aperture and acceptance angle［J］.Proceedings of SPIE，2005，5888：436-443.

M easurement of the polarization Stokes parameters based on photoelastic-modulation and its error analysis

WANGLifu1，WANGZhibin1，2，LIXiao1，2，CHENYouhua1，ZHANGRui1，ZHANGPengfei1
（1.Engineering and Technology Research Center of Shanxi Provincial for Optical-Electric Information and Instrument，North University of China，Taiyuan 030051，China；2.Key Laboratory of Instrument Science＆Dynamic Measurement of Ministry of Education，North University of China，Taiyuan 030051，China）

In order to measure Stokes vectors simply and conveniently，a dual-photoelastic-modulator working at different frequencies was adopted to generate high frequency modulation component loaded with the parameters to be measured after lightmodulation because of the frequency superposition.Four Stokes components suitable for all polarization measurements were obtained once through a phase-locked polarization measurement.After theoretical analysis，simulation verification and error analysis，the effects of phase delay and incidence angle on themeasurement resultswere studied.The results show that all the measured polarization components can be obtained with only one measurement and the method provides theoretical support for further engineering implementation.

spectroscopy；dual-photoelastic modulator；Stokes parameters；polarization；phase-locked

O436.3

A

10.7510／jgjs.issn.1001-3806.2014.02.023

1001-3806（2014）02-0255-05

国家国际科技合作专项基金资助项目（2013DFR10150）；国家自然科学基金仪器专项基金资助项目（61127015）；山西省国际科技合作计划资助项目（2010081038）

王立福（1986-），男，硕士研究生，主要从事弹光干涉具仿真方面的研究。

*通讯联系人。E-mail：wangzhibin＠nuc.edu.cn

2013-06-20；

2013-07-16