基于应力-位移混合有限元法的激光超声数值模拟

许伯强，刘洪凯，徐桂东，徐晨光，李俊敏

基于应力-位移混合有限元法的激光超声数值模拟

许伯强1，刘洪凯2，徐桂东1，徐晨光1，李俊敏2

（1.江苏大学理学院，镇江212013；2.江苏大学机械工程学院，镇江212013）

为了研究激光辐照各向同性半无限大铝材料内超声波的激发和传播特征，采用理想匹配层和应力-位移混合有限元方法建立了半无限大介质中激光激发超声波的有限元数值模型。模拟研究了各向同性半无限大铝材料内激发产生的瞬态波场图和垂直表面位移，并与相同几何模型下采用有限元方法得到的结果进行了对比分析。结果表明，应力-位移混合有限元方法能够有效地消除模型截断边界处的反射波，精确地模拟出无限大固体材料内激光激发超声波的产生和传播特性。数值模拟结果为进一步研究微纳米薄膜材料中皮秒或飞秒激光激发超声波提供了有效的方法。

激光技术；激光超声；理想匹配层；混合有限元；数值模拟

引 言

激光超声具有非接触激发、频带宽和多模态等优点［1-3］，研究激光激发的超声波在材料内的产生和传播特性，能够为材料的物理特性和健康监测提供有效的分析手段，因而在无损检测等领域得到广泛的应用［4-5］。

自1963年WHITE首次证实了脉冲激光辐照金属表面可以激发出高频超声波以来，国内外学者从实验和理论上对激光超声展开了广泛的研究［6］。在数值模拟研究方面，通常采用有限元（finite element method，FEM）数值计算方法［7-8］来分析，有限元数值方法建立在严密的数学理论基础上，能够灵活处理复杂的几何模型，并且能够得到精确的数值解。然而用有限元数值模拟超声波，必须考虑足够大的几何尺寸以避免从边界处超声波反射对计算的影响，这将消耗大量的计算资源和计算时间，降低了计算效率。为了消除或降低有限元计算中截断边界处的反射波的影响，国内外学者做了大量的研究，主要采取两种方法：无反射边界条件法［9］和理想匹配层（perfectly matched layer，PML）［10］等。无反射边界条件方法分析准确度较高，但它需要修改有限元求解程序，无法借助于现有的有限元计算平台执行；1994年，BERENGER［11］在电磁学领域首次提出理想匹配层方法，基于分割场变量方法，将波动方程进行傅里叶变换到频域，再逆变换到时域计算，有效地避免了将频域结果变换到时域结果的卷积运算。这一方法很快被应用到超声波和弹性力学领域［12］。KUCUKCOBAN等人［12］基于PML方法，针对结构力学控制方程，提出将PML的控制函数进行复延拓，经傅里叶变换和逆变换最后得到PML条件下位移-应力场的混合有限元时域方程。这种方法能够有效地消除截断边界处声波的反射，直接得到时域内的波形及瞬态波场图，且求解精度较高。

作者基于应力-位移混合有限元方法，建立激光激发超声波的数值模型，模拟研究了各向同性无限大铝材料中激光超声的产生和传播特征，并与有限元方法获得的结果进行对比分析，取得较为理想的结果。

1 理论分析

考虑均匀的各向同性线弹性材料，线源激光垂直入射到材料表面，计算域的长和宽分别为15mm，如图1所示。为了有效消除激光激发的超声波在边界处的反射所带来的影响，在研究区域Ωr周围添加一定厚度的理想匹配层区域ΩPML来吸收超声波。图中，LPML为PML的厚度，Γ1为对称边界，ΓPML为PML的固定外边界，Γf为自由表面。

Fig.1 Schematic diagram of x，y plane after laser irradiating material surface

为了有效地衰减传播到PML区域的超声波，引入以下复坐标拉伸函数S～，将原空间坐标映射到复空间坐标系统内。

式中，ω为角频率，εs是沿坐标s方向的拉伸函数，s′表示原空间坐标s在积分过程中的积分变量，其表达式为：

1.1PM L混合有限元控制方程

基于平面应变理论，热弹机制下激光激发的超声波在线弹性材料内的控制方程为：

式中，s取x或y。对于超声波而言，实部的作用是对原坐标s的尺度缩放，虚部的作用是衰减进入PML区域的超声波振幅。并且须满足以下条件：

式中，σ，ε，C，α分别为应力、应变、材料的刚度张量和材料的线性热膨胀系数，u为位移矢量；ρ和T分别表示材料的密度和温度；“▽·”，“∶”，上标“T”和变量上标点号“··”分别为梯度算子、内积算符、矩阵转置和对应变量的时间2阶偏导，ΔT为材料受激光辐照引起的温度变化量。

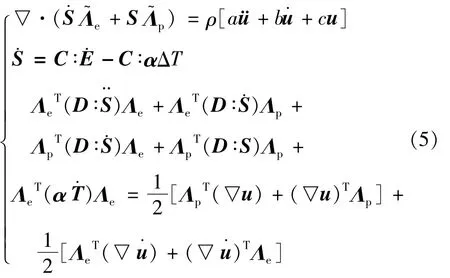
为了在控制方程中引入PML吸收层，时域内的控制方程组（4）式先经过傅里叶变换到频域，然后根据拉伸函数（见（1）式）将原坐标系的微分关系变换到频域方程，即可得到包含PML的频域控制方程；为避免将频域计算结果逆变换到时域的瞬态波的卷积运算，以便在时域内对激光激发超声波进行瞬态分析，将PML形式的频域控制方程组经过傅里叶逆变换回时域内求解，得到以下应力-位移混合有限元的时域控制方程：式中，D为材料的柔度矩阵（刚度矩阵C的逆）；系数a，b，c和矩阵，，Λe，Λp为推导过程中得到的包含模型缩放因子和衰减因子的量，它们的表达式见参考文献［13］；“·”和“··”分别表示对应变量的时间1阶偏导和2阶偏导。上述变换中，引入了应力的时间积分形式S（x，y，t）＝（x，y，τ）dτ和应变的时间积分形式E（x，y，t）＝∫t0ε（x，y，t）dτ作为新的未知变量来降低方程的阶数。

边界条件可表示为：

初始条件为：

1.2网格和时间步长

在混合有限元数值模拟计算中，时间步长的选取和模型网格大小的划分直接影响计算的精确性、稳定性和计算效率。一般情况下，选择越小的时间步长得到的计算结果越精确，但是却会让求解过程过于漫长，降低了计算效率；但是过长的时间步长又会导致求解的高频部分出现较大的误差而降低计算精度。因此，在数值计算中，假设在计算区域内时间离散误差都不超过δ，那么就要求时间步长必须满足以下条件［7］：

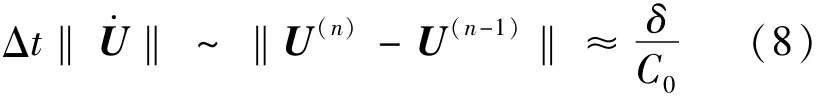
式中，δ为时间离散误差，C0常数，U（n－1）是对应某一时刻t给定的解向量，并将其作为下一个计算时间步长的初始条件，通过计算求得t＋Δt时刻的解向量U（n）。

结合时间步长，为了使各个计算的波形达到合适的精度要求，网格单元大小l的选择应该满足以下表达式：

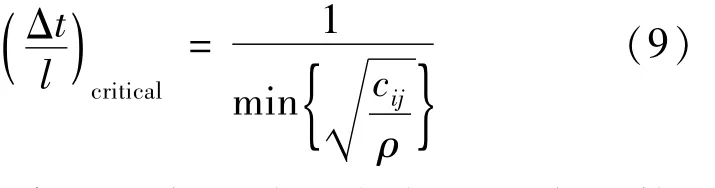
式中，l为网格单元尺寸，cij表示材料的刚度系数，是材料内激发的超声波最小波速。

采用变网格技术，在激光辐照区域设定网格大小为5μm，在远离激光辐照区域设定网格大小为100μm。初始时间步长设定为0.1ns，根据迭代精度在计算过程中调整时间步长，最大时间步长不超过10ns，给定计算误差为δ＝10－4。选择瞬态线性直接求解器进行求解。

1.3材料、激光和PM L参量设置

作者采用傅里叶热传导理论来描述激光辐照材料表面所产生的温度场分布，计算中采用输出波长为1064nm的高斯型激光，考虑材料的表面的吸收系数和光穿透效应，材料吸收激光能量表达式为：

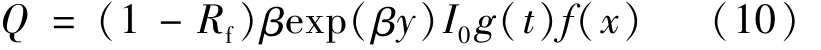
式中，Rf为材料表面对光的反射率，那么在材料表面对激光能量的吸收系数为（1－Rf）；β为激光能量在材料深度方向的衰减系数（其倒数1／β为材料对激光的光趋肤深度）；I0为激光辐照区域中心的能量密度；g（t）和f（x）分别为激光能量在时域和空间的分布函数：

式中，τ和r分别为脉冲激光的脉宽和辐照线源半宽。辐照激光能量的时域和空间分布示意图如图2所示。

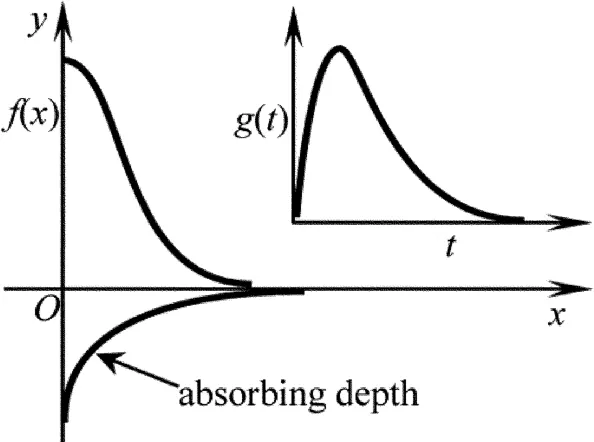
Fig.2 Spatial and temporal profile of the heat source due to line-focused laser illumination

忽略材料同外界的热交换，傅里叶热传导方程的边界条件为n·（－k▽T）＝0，其中k，n分别为热传导率和单位法向量。设定材料的初始温度为T（x，y，0）＝300K。

本文中采用脉宽为10ns、辐照线源半宽为300μm和能量密度为4.0MW／cm2的入射激光光源，采用铝板作为模型材料，其光反射率Rf＝0.85，光趋肤深度为40μm。计算中材料的热学和力学参量如表1所示。当材料参量为已知量时，PML的尺度缩放和衰减因子［13］的参量设置只由单一的变量R来控制，设定反射率为R＝10－8，PML的厚度为LPML＝3mm。

Table 1 Thermal and mechanical parameters of aluminum

2 数值模拟结果及讨论

为了精确的模拟激光辐照铝材料表面时超声波的产生和传播特性，首先需要得到精确的激光辐照所产生的温度场分布。数值模拟过程中激光能量输入可看作体热源。图3中给出了激光与铝材相互作用后激光辐照中心（x＝0μm）不同深度处温度随时间的变化曲线。

Fig.3 Temperature distributions at different depths at laser irradiation center

图3显示，在激光辐照中心表面（x＝0μm，y＝0μm）和表面下方10μm（x＝0μm，y＝－10μm）处，材料的温度在大约70ns时达到最大值，之后由于热传导作用随时间缓慢下降。在激光辐照中心表面下方50μm（x＝0μm，y＝－50μm）和100μm（x＝0μm，y＝－50μm）由于超过了光趋肤深度的范围，主要受热传导的作用而呈现出温度缓慢上升的趋势。这些激光中心表面下不同深度处的温度随时间的变化曲线特征很好地与作者之前研究［8］的有限元数值模拟结果相吻合，充分说明了应力-位移混合有限元模型中温度场计算的准确性。这种非均匀温度场等效于热弹体力源，是激发产生超声波的直接驱动力。

Fig.4 Wave snapshots of total displacement at in semi-infinite aluminum

图4中给出了利用应力-位移混合有限元方法在半无限大铝材料内不同时刻的总位移场。图4a显示在半无限大铝材料内激光激发产生的超声波包括纵波P、横波S、头波H和Rayleigh表面波R。从图中可以看出P波的传播速率最快，在2.0μs时已经到达PML与研究区域的分界面处，并且在图所示的右上角和左下角处已经有比较明显的衰减；图4b中的虚线1和虚线2显示在4.2μs时，部分H波和S波已经传播到PML区域并且有很明显的衰减，R波也已经到达PML区域与研究区域的边界，此时P波已经被PML区域完全吸收；对比图4c与图4b可以明显地看出，在4.6μs时H波和S波的衰减更加明显，R波也进入到PML区域中，并且有明显的衰减；随着时间的推移，5.2μs时几乎所有的波都被PML区域完全吸收，只残留部分横波在材料内继续传播。由此可见，这种PML混合有限元方法能够有效地衰减进入PML区域的超声波，从而消除或降低超声波在PML区域外边界处的反射，以此精确模拟半无限大介质内激光激发超声波的数值模型，并且利用这种方法能够得到频域分析方法所无法得到的全场位移波场图，实现结果分析的直观化、可视化。

图5是分别采用应力-位移混合有限元方法和有限元方法所获得垂直表面位移波形图。图5a～图5d分别是在距离激光辐照中心2mm，6mm，8mm和12mm处的波形图，其中实线表示采用应力-位移混合有限元方法（mixed finite element method，MFEM），虚线表示采用有限元方法（FEM）。两种方法采用同样的几何模型：15mm宽、15mm高，所不同的是，应力-位移混合有限元方法包含3mm厚的PML区域。由图可知，激光激发超声波在铝材表面产生的垂直表面位移波形包含3种模态：掠面纵波Sp，表面横波Ss和单极性Rayleigh波R。由图可见掠面纵波的传播速率最快，最先到达探测点，其次是表面横波，传播速率最慢的是Rayleigh波，由于表面横波和Rayleigh波的波速相差不大，接收到波形显示Rayleigh波和表面横波基本叠加在一起（如图5a所示）；掠面纵波的振幅比较小，并且随着传播距离的增加有明显的衰减，Rayleigh波的振幅比较大，且其幅度几乎不随传播距离的增大而衰减；根据Sp波和R波的波峰到达探测点2mm，6mm，8mm和12mm时的时间可以计算出它们的波速分别为5797.1m／s和2857.1m／s；这与它们的理论计算得出的相速率非常接近。由于Sp波和R波的相速度相差很大，随着传播距离的增大，两个波的波形彼此逐渐分离。然而由图5a～图5d中虚线部分显示的波形图可见，波形已经受反射波的影响而出现形态变化，距离边界越近的探测点越早被反射波影响，并且影响的程度越大；由于Rayleigh波的振幅比较大，在波形中占主导地位，所以明显地看出反射的Rayleigh波Rr是反射波的主要成分。从图5a～图5d中实线部分的波形与利用大尺寸几何模型情况下的FEM［14］计算结果取得较好的一致，且来自边界处的反射波形明显消除。并且应力-位移混合有限元方法的模拟结果与1996年DOYLE和SCALA［15］在实验上得到的Rayleigh波波形吻合得非常好。

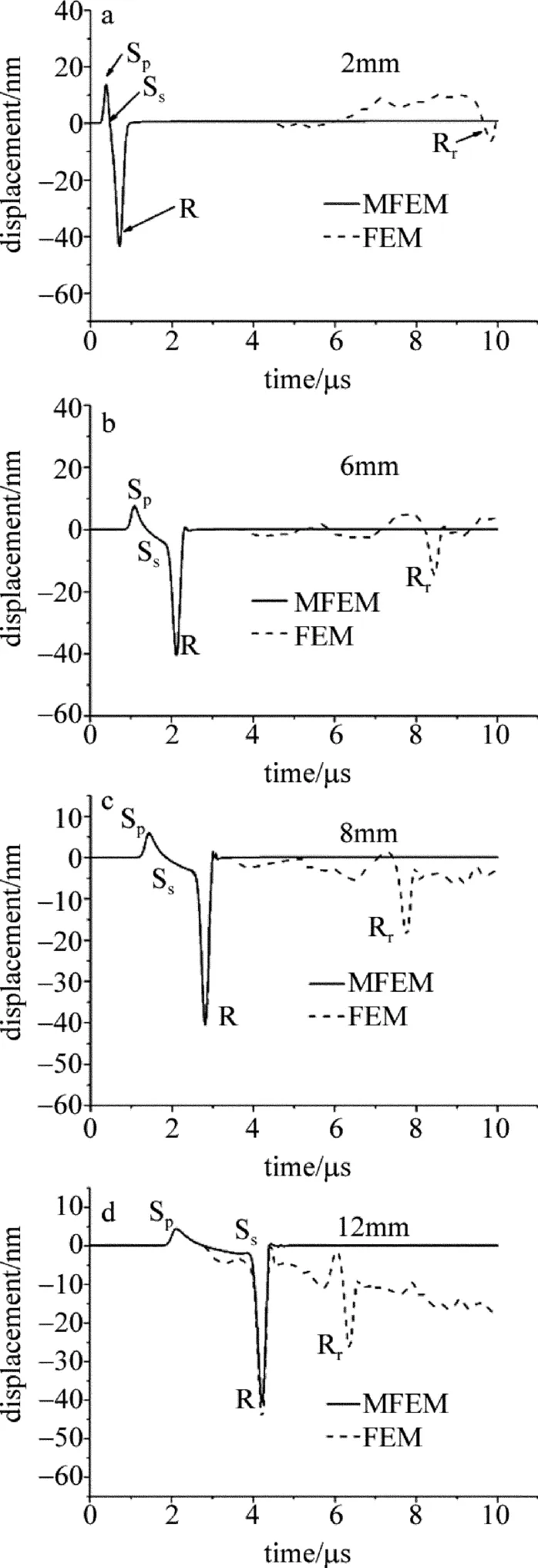
Fig.5 Surface normal displacement waveforms at different distances of 2mm，6mm，8mm and 12mm in aluminum by using finite element method and mixed finite element method，respectively

3 结 论

基于应力-位移混合有限元方法，建立了各向同性半无限大线弹性材料中激光激发超声波的数值模型，得到了材料表面的垂直表面位移波形及全场波场图。计算结果说明，激光在各向同性半无限大材料内同时激发出纵波、横波、头波和Rayleigh波。与有限元方法相比，这种应力-位移混合有限元方法有效地消除边界处的反射波，能够有效地降低模型的尺寸和节省计算资源，并能精确地模拟激光超声波在材料内的产生和传播特征。数值模拟结果为进一步研究微纳米薄膜材料中皮秒或飞秒激光激发超声波提供了有效的方法。

［1］ ROSSIGNOL C，PERRIN B，LABORDE S，et al.Nondestructive evaluation of micrometric diamond films with an interferometric picosecond ultrasonics technique［J］.Journal of Applied Physics，2004，95（8）：4157-4162.

［2］ KUNDU T.Ultrasonic nondestructive evaluation：engineering and baiological material characterization［M］.Boca Raton，Florida，USA：CRC Press，2004：435-494.

［3］ DAIY，XU B Q，LOU Y，et al.Finite element modeling of the interaction of laser-generated ultrasound with a surface-breaking notch in an elastic plate［J］.Optics＆Laser Technology，2010，42（8）：693-697.

［4］ SOHN Y，KRISHNASWAMY S.Scaning laser line source technique using monopolar Rayleigh waves［J］.American Institute of Physics，2004，700（1）：278-285.

［5］ LIU JS，XU ZH，GU G Q.Numerical study on improvement of signal-to-noise ratio of surface acoustic waves based on laser array［J］.Laser Technology，2011，35（3）：403-406（in Chinese）.

［6］ SUN H X，XU B Q.Numerical analysis of laser-generated lamb wave by finite element method in time and frequency domain［J］.Chinese Journal of Lasers，2010，37（2）：537-542（in chinese）.

［7］ JOHNSON C.Numerical solution of partial differential equations by the finite element methods［M］.New York，USA：Cambridge University Press，1987：14-48.

［8］ XU B Q，SHEN Z H，WANG JJ，et al.Thermoelastic finite element modeling of laser generation ultrasound［J］.Journal of Applied Physics，2006，99（3）：033508.

［9］ GIVOLID，KELLER JB.Non-reflecting boundary conditions for elastic waves［J］.Wave Motion，1990，12（3）：261-279.

［10］ BASU U，CHOPRA A K.Perfectly matched layers for transient elastodynamics of unbounded domains［J］.International Journal for Numerical Methods in Engineering，2004，59（8）：1039-1074.

［11］ BERENGER JP.A perfectly matched layer for the absorption of electromagnetic waves［J］.Journal of Computational Physics，1994，114（2）：185-200.

［12］ FESTAG，NIELSEN S.PML absorbing boundaries［J］.Bulletin of the Seismological Society of America Definition，2003，93（2）：891-903.

［13］ KUCUKCOBAN S，KALLIVOKASL F.Mixed perfectly matched layers for direct transient analysis in 2-D elastic heterogeneous media［J］.Computer Methods in Applied Mechanics and Engineering，2011，200（1／4）：57-76.

［14］ XU B Q，SHEN Z H，NIX W，et al.Numerical simulation of laser-generated ultrasound by the finite element method［J］.Journal of Applied Physics，2004，95（4）：2116-2122.

［15］ DOYLE PA，SCALA CM.Near-field ultrasonic Rayleigh waves from a laser line source［J］.Ultrasonics，1996，34（1）：1-8.

Mixed stress-displacement finite element method for laser-generated ultrasound

XUBaiqiang1，LIUHongkai2，XUGuidong1，XUChenguang1，LIJunmin2
（1.Faculty of Science，Jiangsu University，Zhenjiang212013，China；2.School of Mechanical Engineering，Jiangsu University，Zhenjiang 212013，China）

In order to study the generation and propagation of laser-generated ultrasound in isotropic semi-infinite aluminum material，a laser-generated ultrasound in an arbitrary elastic semi-infinite medium model was established by using mixed stress-displacement finite element method and perfectly matched layer（PML）.The transient wave snapshots and surface normal displacement waveforms in semi-infinite aluminum materials were obtained.The surface normal displacement waveforms were compared with the same geometrical finite element model.The results show that the mixed stressdisplacement finite element method can effectively eliminate reflection waves from truncated boundary，and simulate the generation and propagation of ultrasound in semi-infinite solid material accurately.The simulation results provide an effective method for research of the laser-generated ultrasound waves in micro-nanostructure by picosecond or femtosecond laser irradiation.

laser technique；laser-generated ultrasonic；perfectly matched layer；mixed finite element method； numerical simulation

O426.1；O411.3

A

10.7510／jgjs.issn.1001-3806.2014.02.018

1001-3806（2014）02-0230-06

国家自然科学基金资助项目（11172114）；江苏省高校自然科学研究资助项目（10KJA140006）；江苏省六大人才高峰资助项目（2012-ZBZZ-027）

许伯强（1963-），男，博士，博士生导师，现主要从事超声无损检测的研究。

E-mail：bqxu＠ujs.edu.cn

2013-04-11；

2013-04-23