卫星振动引起的非规则采样降质图像复原方法

智喜洋，张 伟，李立源，孙 晅

（哈尔滨工业大学空间光学工程研究中心，150001哈尔滨）

卫星振动引起的非规则采样降质图像复原方法

智喜洋，张 伟，李立源，孙 晅

（哈尔滨工业大学空间光学工程研究中心，150001哈尔滨）

针对卫星振动引起的TDICCD相机非规则采样导致像质退化的问题，提出了非规则采样降质退化图像的复原方法.首先利用基于非均匀快速傅里叶变换的频域插值对非规则采样的几何降质退化规律进行建模，并结合遥感成像的模糊退化过程，建立非规则采样降质图像退化模型.然后利用频域插值特性将模型逆求解过程转换为Toeplitz矩阵系统的线性方程求解问题，实现了快速求解，提出非规则采样几何降质和模糊退化的综合处理方法.最后利用测试图形和真实遥感图像对方法进行验证，实验结果表明：在严重模糊、几何降质及高噪声水平条件下，复原后的图像与理想图像的结构相似度仍优于0.93，而且具有较高的处理效率.该方法能有效应用于在轨振动引起的非规则采样降质的复原处理.

卫星振动；非规则采样；几何降质；退化模型；图像复原

随着航天光学遥感载荷技术的不断发展，空间相机的分辨率越来越高.然而，卫星在轨运行期间，平台的各种振动会引起相机光轴指向的抖动，从而影响高分辨率相机的成像质量，特别是对于目前被广泛应用的线阵推扫式TDICCD相机而言，振动在多级时间积分内所致的图像像移，不仅会引起图像的模糊，而且还会造成探测器像元采样的非规则性，从而引起图像非规则性的几何降质，这将严重影响相机的高分辨率成像能力和高精度测绘能力.

限于高精度姿态稳定控制、稳像和减振等技术的现有工艺水平，通常采用图像复原的方法来补偿振动像移引起的像质退化.国内外学者在遥感图像退化模型和复原方面已取得了大量的研究成果，但研究工作大多是针对模糊退化的图像复原［1-5］，在振动所致的几何降质复原方面，尽管初步开展了基于不同插值算法和各种约束条件的几何校正算法的研究［6-11］，但尚未从振动所致TDICCD相机像移对几何成像质量的影响机理出发，将非规则采样造成的几何降质引入遥感图像退化模型，因此无法实现对模糊和非规则性几何降质退化图像的综合提升处理.而且，在几何校正插值算法的求解方面仍存在运算速度较慢的问题.

本文从卫星振动引起的TDICCD相机非规则采样的角度出发，重点分析了振动导致非规则采样的几何降质退化过程及规律，并对几何降质的图像退化进行建模，将其引入已有的遥感图像退化模型，建立了更为完整的TDICCD非规则采样图像的像质退化模型，在此基础上提出了一种图像模糊和非规则性几何降质退化综合处理的复原方法.同时，为了提高复原算法的运算效率，在退化模型逆求解的过程中，通过采用基于非均匀快速傅里叶变换的频域插值，构造了具有特定循环结构的Toeplitz系统，从而将求解过程转换为基于Toeplitz矩阵的线性方程系统求解问题，实现了模型方程求解的快速运算.

1 卫星振动引起非规则采样像质退化

卫星在轨工作期间，卫星平台及星上活动部件的各种运动均会引起相机光轴指向的抖动，这将导致相机在积分成像过程中产生图像像移，从而影响相机的成像质量.卫星振动的形式较为复杂，但通常可以近似分解为若干正弦振动的叠加［12］:式中fi，Ai，φi分别为第i个谐波分量的振动频率、振幅和初始相位，t为卫星摄影时刻．

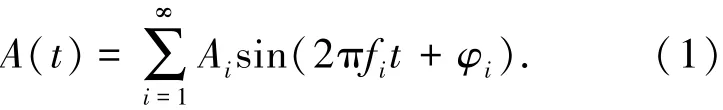
TDICCD相机推扫成像采样过程中，图像各行不是同一时刻采样得到的，而是由相机在不同成像时刻获得［13］，因此积分成像过程中的振动像移不仅会导致图像的模糊，还会引起像元积分中心位置的偏移，而且各行像元对应的偏移量可能存在一定的差异，这将导致探测器像元采样位置的非规则性，表现为图像非规则性的几何变形.根据公式（1），可以得出非规则采样位置的数学表达为

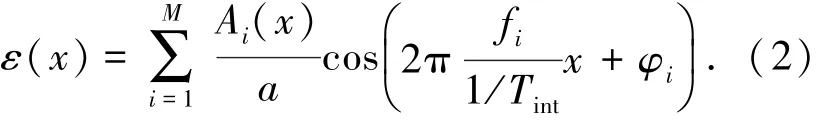
式中:ε为像元采样位置的偏移量；a为像元尺寸；Tint为TDICCD单级积分时间；f1，f2，…，fM为振动频率分量，且f1＜f2＜…＜fM，fM为探测器采样的奈奎斯特频率．

假设探测器像元在像平面的理想采样位置为λmn=（xmn，ymn）=（m，n），振动像移引起的像元中心位置偏移量ε（m，n）=（εx（m，n），εy（m，n）），则像元在像平面的实际采样位置Λ=｛λmn｝M，Nm=1，n=1⊆R2:

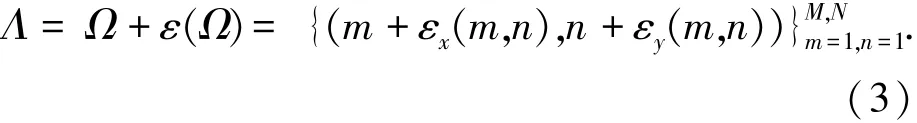
式中Ω=（［1，M］×［1，N］）∩Z2为理想采样位置．

图1示意了像元的理想采样位置和非规则采样的实际情况.从图1（b）中可以看出，非规则采样后的图像产生了明显的逐行偏移.

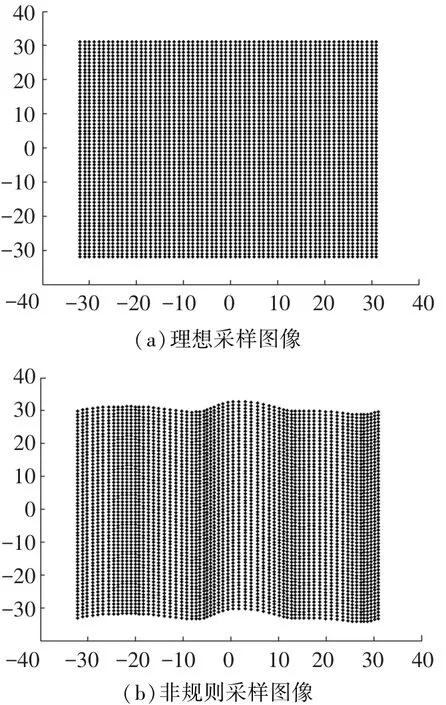
图1 理想采样与非规则采样图像的对比

2 TDICCD非规则采样像质退化模型及图像复原方法

2.1 非规则采样遥感图像退化模型

一般情况，遥感图像退化模型描述如下［14］:

式中:Y表示遥感成像系统获取的像质退化图像；X表示原始场景图像，即理想的无退化图像；h表示遥感成像链路中大气环境、光学系统、探测器、成像电子学、卫星平台等各环节引起的模糊退化；n表示成像过程中引入的噪声；∗表示卷积．

经上述分析可知，TDICCD相机非规则采样引起几何降质的图像退化可建模为

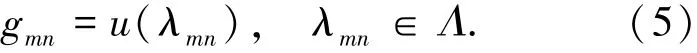
式中:g:Λ→R表示非规则采样图像；u:R2→R表示原始场景图像．

此时，离散化的式（4）可写为

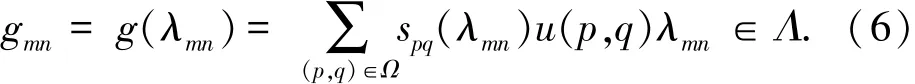
式中spq（λmn）表示对原始场景图像u的非规则重采样，能够表征振动所致非规则采样引起的空间移变几何降质退化，可通过拉格朗日插值、自适应插值和频域插值等方法实现．

若令λk=λmn当且仅当k=（n-1）N+m时成立，即λk是λmn按列排序，且gk、si与ui同理．则式（6）改写为

令Sspac=｛ski｝为重采样矩阵，且满足ski=si（λk），则式（7）的矩阵形式为

采用频域插值作为重采样方法，令＾u为u在频域上的表达，则式（8）改写为

式中Sfreq表示从频域到空域的插值，简记为S．

进一步，将非规则采样引起的几何像质退化引入传统的遥感图像降质退化模型（式（4）），建立完整的非规则采样图像的像质退化模型为

式中H表示h对应的模糊算子．

可见，该模型既能够表征遥感成像过程中各环节引起的模糊退化，又能够表征TDICCD非规则采样引起的几何像质退化.非规则采样图像的复原问题就是利用g、H和n估计原始场景图像u．

2.2 非规则采样遥感图像复原方法

非规则采样图像复原问题即是对像质退化模型（式（10））的逆求解，可通过如下最小化问题的求解实现［15］:

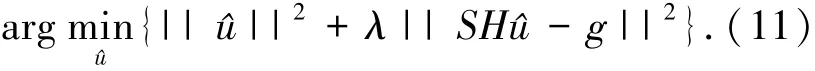
式中λ为拉格朗日乘子．则图像复原的求解问题转换为

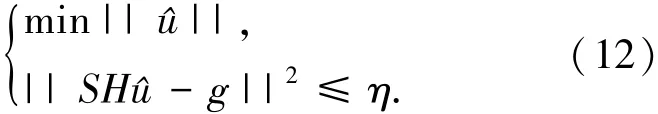
即在满足约束条件｜｜SH＾u-g｜｜≤η的情况下，寻找＾u的最优解，因此解可以通过逼近式（13）得到:

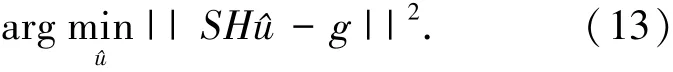
引入权重矩阵W，其法方程为

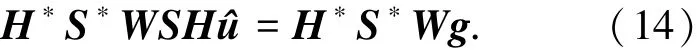
式中:∗表示共轭转置，W用于均衡采样不均匀对方程组条件数的影响．假设空域坐标（k，l），采样位置落在矩阵区域［k，k+1］×［l，l+1］的像元有nkl个，则该区域像元权重W=diag｛wi｝满足条件wi=1／nkl．

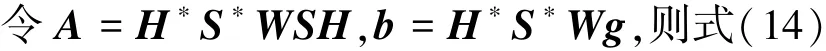
简记为

因为A是对称正定阵，因此利用共轭梯度法逼近式（15）的解．显然，只要选择适当的迭代终止条件，就可以近似求得最优解＾up，对其进行快速傅里叶逆变换，即得到理想图像的估计．

2.3 图像复原方法的快速求解

令T=S∗WS，S表示频域到空域的插值，∗表示共轭转置，S∗表示空域到频域的插值，实际运算取S∗=（1／N2）｛ski｝∗进行归一化，W为对角矩．

为了实现方程（15）的快速求解，本文采用了基于非均匀快速傅里叶变换的频域插值方法［16-17］．事实上，当S为此类算法时，根据矩阵运算法则得出:

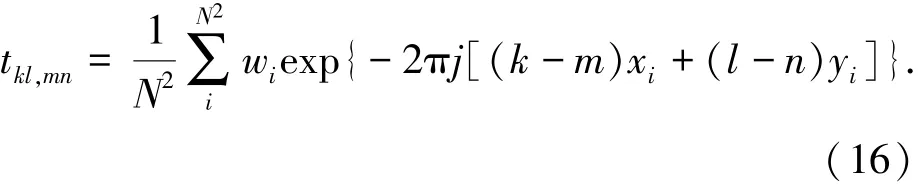
式中:k，l，m，n∈［1，N］∩Z；k，l对应矩阵S∗；m，n对应矩阵S．

此时:注意到T是Toeplitz分块矩阵，T中具有一定的循环结构．这样，可以通过对T矩阵进行扩展，从而构造循环矩阵:

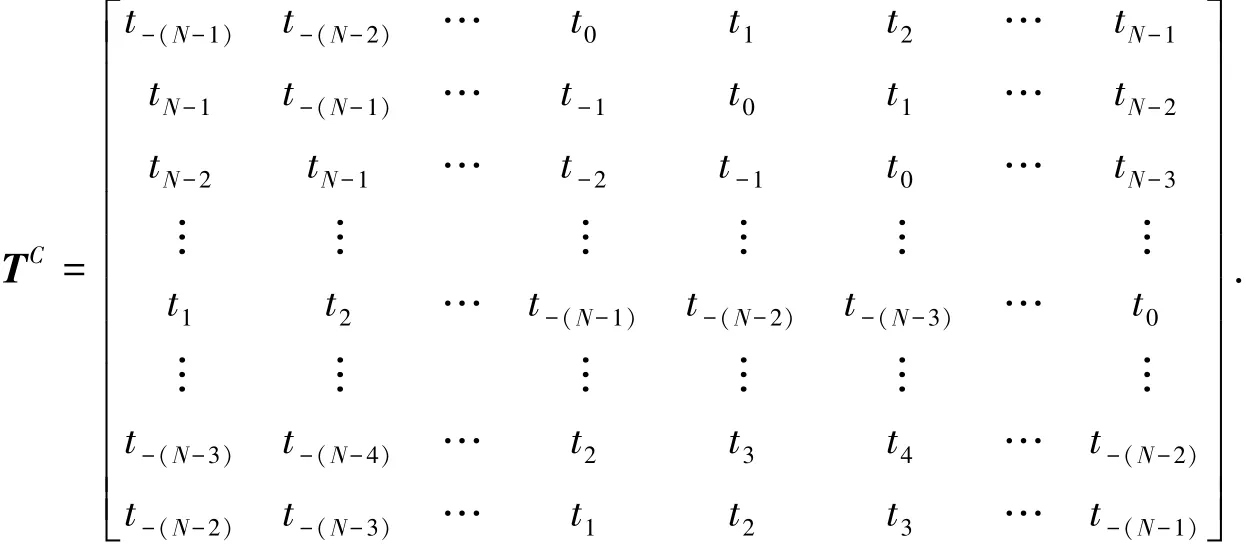
事实上，假设a为列向量，则Ta的求解问题即可转化为

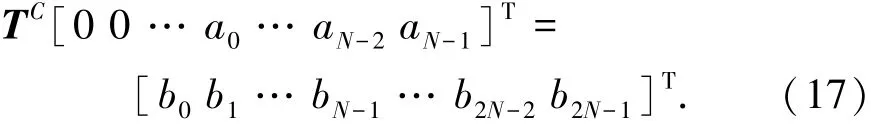
式中T表示矩阵转置.

因此，方程（15）即可转换为基于Toeplitz矩阵系统的线性方程系统［18］，这样就可以利用快速傅里叶变换进行快速计算［17］，其输出结果的上半部分｛bi｝N-1i=0即为Ta运算结果，实现了复原问题的快速运算．

3 仿真实验及分析

3.1 像质退化图像仿真

利用式（10）仿真TDICCD推扫成像过程，模拟生成不同程度模糊、非规则性几何降质和噪声条件下的标准场景退化图像.标准场景是采用经过几何精校正后的高分辨率卫星图像，即认为没有任何几何变形，并且对原始图像进行了4倍欠采样，以消除原始图像中模糊与噪声的影响.

考虑到对于光学遥感图像而言，图像模糊通常可近似为高斯模糊形式，而绝大多数噪声都可用均值为0、方差各异的高斯白噪声模型来表示，因此本文通过加入模糊核α∈［10-4，4×10-4］的高斯型模糊函数和标准差σ∈［0.25，1］的加性高斯白噪模拟不同模糊和噪声引起的像质退化．并采用式（2）模拟振动所致像元非规则采样引起的几何降质退化．

3.2 图像复原的客观评价方法

结构相似度（structural similarity，SSIM）［19-20］是一种衡量两幅图像相似程度的全参考评价方法，相比较传统的峰值信噪比和均方误差评价方法，SSIM将图像的亮度、对比度和结构信息作为3个相互独立的评价标准来比较，图像的对比度能够很好地反映图像的模糊程度，而结构信息能够很好地反映图像的几何失真程度.因此，采用SSIM来评价复原方法的处理效果，既可以对不同类型的图像退化，有针对性的选择一种评价标准，实现模糊或几何降质退化处理情况的独立评价，又可以选择三者或两者结合的方式，实现算法对模糊与几何降质退化综合处理情况的评价.

在复原算法实验中，采用SSIM并结合主观视觉作为评价依据，对比分析复原方法在不同场景对象与像质退化条件下的复原结果，复原后的图像与标准场景图像的SSIM值越大，说明复原方法的处理效果越好.并且，通过统计复原算法的处理迭代次数和运算时间，分析算法的运算效率.

3.3 实验验证与分析

为了直观显示图像复原方法对几何像质退化的复原效果，首先设计了两个测试图形，分别为垂直与水平方向、45°与135°方向间距递变的多条亮条纹构成的线型网格，并结合3.1节仿真生成不同振动情况下相机非规则采样的图像，如图2（a）和（b）所示，图中的亮条纹出现了明显的几何扭曲.

利用本文提出的复原算法进行处理，复原结果如图2（c）和（d）所示.从视觉效果明显看出，复原后图像中的亮条纹已无明显几何变形，恢复了测试图形本来的面貌.

图2 测试图形图像复原实验

下面结合3.1节仿真生成的多组标准场景退化图像（图像大小为512×512），并通过与传统复原算法处理结果的对比，进一步验证复原算法的有效性.图3（a）和（b）列出了两组包含较为严重模糊、非规则性几何降质和噪声条件下的退化图像.图3（c）和（d）、（e）和（f）分别为采用针对模糊退化［4］和几何降质复原算法［7］的图像复原结果.图3（g）和（h）为采用本文提出的复原算法的图像复原结果，对比图中方框区域处理前后的视觉效果可明显看出:传统的复原算法无法实现图像模糊和非规则几何降质的综合处理，而本文提出的复原算法能够有效增强原退化图像中的边缘锐度和细节信息的同时，还能够很好地消除图像中的几何扭曲.

表1～2列出了利用SSIM对复原前后图像质量的客观评价结果.表中OSSIM、PSSIM分别表示标准场景图像（理想图像）与退化图像、复原后图像的SSIM值.

图3 标准场景图像复原实验

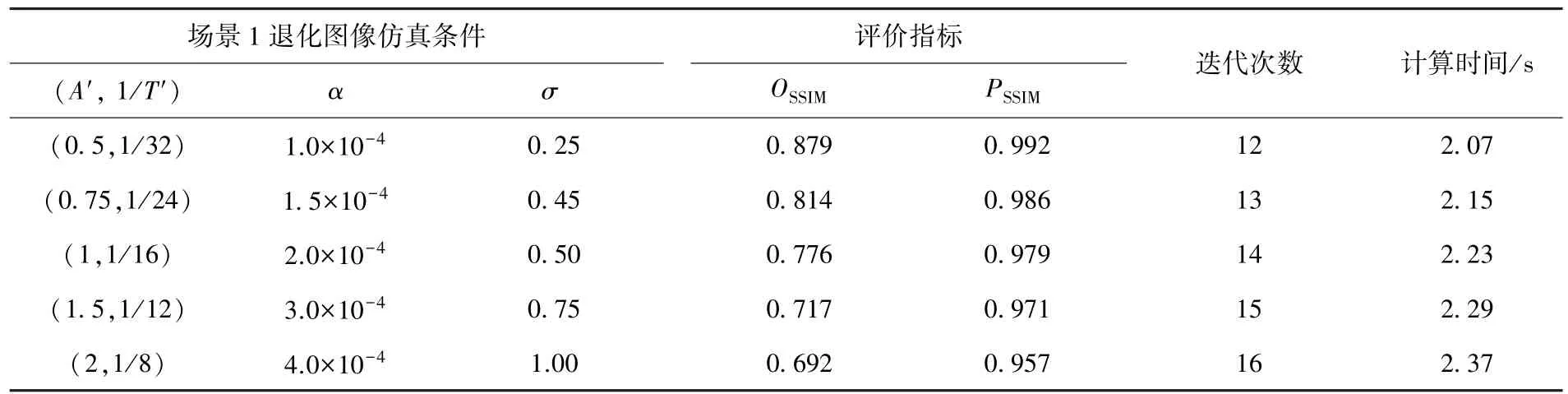
表1 场景1退化图像的仿真条件与复原结果

表2 场景2退化图像的仿真条件与复原结果

由表1～2可见，对存在不同程度模糊、非规则性几何变形和噪声的仿真退化图像，复原算法均能够有效提升SSIM，甚至在严重模糊、几何变形和高噪声水平的条件下，复原后的图像与标准场景图像（理想图像）的SSIM值仍优于0.93.并且，当图像大小为512×512时，复原算法能够通过20次左右迭代，在数秒内达到最优解，实现非规则采样退化图像的复原处理，具有较高的运算效率.

4 结 论

1）分析了卫星振动导致的TDICCD相机非规则采样对几何成像质量的影响规律，并通过基于非均匀快速傅里叶变换的频域插值对其建模引入遥感图像退化过程，从而建立了更为完善的非规则采样遥感图像退化模型，在此基础上提出了一种更适合于航天TDICCD相机振动降质图像处理的复原方法.

2）利用非均匀快速傅里叶变换的频域插值特性构造了具有特定结构的循环矩阵，将退化模型逆求解过程转换为Toeplitz矩阵线性方程求解问题，从而基于Toeplitz矩阵系统方程理论，给出了模型逆求解的快速运算方法，使复原算法具有较高的运算效率.

3）对不同场景类型和降质条件的遥感退化图像复原结果进行了比较评价，结果表明本文提出的复原方法既能够有效的去除图像的模糊，也能够对振动所致非规则采样引起的几何降质进行较好处理，在严重模糊、几何变形和高噪声水平的条件下，复原后的图像与理想图像的SSIM值仍优于0.93.并且，复原算法具有较高的处理速度.

［1］HADAR O，DROR I，KOPEIKA N S.Numerical calculation of imagemotion and vibrationmodulation transfer functions-a new method［C］／／International Society for Optics and Photonics.San Diego，CA:［s.n.］，1991:61-74.

［2］STERN A，KOPEIKA N S.Analyticalmethod to calculate optical transfer functions for image motion and its implementation in vibrated image restoration［C］／／Nineteenth Convention of Electrical and Electronics Engineers in Israel，1996.Piscataway:IEEE，1996: 379-382.

［3］STERN A，KOPEIKA N S.Optical transfer function analysis of images blurred by non-harmonic vibrations characterized by their power spectrum density［J］. Journal of the Optical Society of America A:Optics Image Science and Vision，1999，16（9）:2200-2208.

［4］YANG H L，HUANG P H，LAISH.A novel gradient attenuation Richardson-Lucy algorithm for image motion deblurring［J］.Signal Processing，2014（103）:399-414.

［5］耿文豹，翟林培，丁亚林.振动对光学成像系统传递函数影响的分析［J］.光学精密工程，2009，17（2）: 314-320.

［6］GRÖCHENIG K，STROHMER T.Numerical and theoretical aspects of nonuniform sampling of band-limited images［J］. Nonuniform Sampling，Information Technology:Transmission，Processing，and Storage.Berlin:Springer，2001:283-324.

［7］CHEN H C，WANGW J.Locally edge-adapted distance for image interpolation based on genetic fuzzy system［J］.Expert Systems with Applications，2010，37（1）: 288-297.

［8］Le FLOCH H，LABIT C.Irregular image sub-sampling and reconstruction by adaptive sampling［C］／／International Conference on Image Processing. Piscataway:IEEE，1996，3:379-382.

［9］KEYW R.Cubic convolution interpolation for digital image processing［J］.Acoustics，Speech and Signal Processing，1981，29（6）:1153-1160.

［10］VAZQUEZC，DUBOISE，KONRAD J.Reconstruction of nonuniformly sampled images in spline spaces［J］. IEEE Transactions on Image Processing，2005，14（6）: 713-725.

［11］TAM W S，KOK C W，SIU W C.Modified edgedirected interpolation for images［J］.Electronic Imaging，2010，19（1）:013011-1-013011-20.

［12］HOLST G C.Electro-optical imaging system performance［M］.Bellingham，Washington:Winter Park，Florida and SPIE press，2003.

［13］FIETE R D，TANTALO TA.Image quality of increased along-scan sampling for remote sensing systems［J］. Optical Engineering，1999，38（5）:815-820.

［14］ANDREWSH C，HUNT B R.Digital image restoration［M］.Englewood Cliffs，NJ:Prentice-Hall，1977.

［15］CHAMBOLLE A.An algorithm for total variation minimization and applications［J］.Journal of Mathematical Imaging and Vision，2004，20（1／2）:89-97.

［16］BEYLKIN G.On the fast Fourier transform of functions with singularities［J］.Applied and Computational Harmonic Analysis，1995，2（4）:363-381.

［17］POTTSD，STEIDLG，TASCHEM.Fast fourier transforms for nonequispaced aata:a tutorial［M］.Boston: Birkhäuser，2001:247-274.

［18］BRENT R P，GUSTAVSON F G，YUN D Y.Fast solution of Toeplitz systems of equations and computation of Padéapproximants［J］.Journal of Algorithms，1980，1（3）:259-295.

［19］WANG Z，BOVIK A C，SHEIKH H R.Image quality assessment:from error visibility to structural similarity［J］.Image Processing，2004，13（4）:600-612.

［20］LIC，BOVIK A C.Three-componentweighted structural similarity index［C］／／IS＆T／SPIE Electronic Imaging，International Society for Optics and Photonics. Bellingham WA:SPIE，2009:72420Q-1-72420Q-9.

（编辑张 宏）

Restoration of irregularly sampled image degradation due to satellite vibrations

ZHIXiyang，ZHANGWei，LILiyuan，SUN Xuan

（Research Center for Space Optical Engineering，Harbin Institute of Technology，150001 Harbin，China）

A new method is proposed to solve a problem of image restoration which would be degraded by TDICCD irregular sampling process owning to satellite vibrations.Firstly，the rules of image geometric quality degradation ismathematicallymodeled using unequally spaced fast Fourier transform（USFFT）interpolation，and then a full image degradation model is developed combined with the blurred degradation process. Subsequently，the inverse solution problem of the model equations is transformed into a system of linear equationswith a Toeplitzmatrix as system matrix on the basis of the USFFT interpolation characteristics.And then the equations can be sovled efficiently.Then，a new method of image restoration is presented，which can implement not only deblurring but also irregular to regular sampling.Finally，the method is verified using simulated standard pattern and real remote sensing images.Experimental results indicate that the proposed method is able to improve the irregularly sampled image effectively，and ithas fast computation.The Structural Similarity index between the restored and ideal images is no less than 0.93 in the case of seriously blurred，irregularly sampled and noisy images.The proposed approach can be applied to restore the irregular sampling images owning to on-orbit vibrations effectively.

satellite vibrations；irregular sampling；geometric degradation；degradationmodel；image restoration

TP751.1

A

0367-6234（2014）09-0009-06

2013-10-22.

国家自然科学基金资助项目（61007008）.

智喜洋（1982—），男，讲师；张 伟（1962—），男，教授，博士生导师.

张 伟，wzheng5＠hit.edu.cn.