基于矩阵重构的功率倒置算法研究

任 远 刘 翔 罗丁利

(西安电子工程研究所 西安 710100)

0 引言

GPS(Global Position System)是美国在1973年开始研制的卫星导航与定位系统，具有高精度、全天候、全球覆盖、方便灵活等特点。时至今日，GPS系统已广泛应用在军事、航天、航空、测绘、通讯等各个行业，为美国带来了巨大的经济和军事效益，也引起了世界各国对全球定位导航系统的密切关注;憧憬于非常广阔的应用前景和巨大的商业市场，中国、俄罗斯、欧盟、日本都在发展自己的卫星定位导航系统。采用码分多址的GPS信号具有一定的抗干扰能力，但是由于 GPS卫星距离地球表面大约20000km，加之信号发射功率低，GPS接收机天线接收到的GPS信号强度低于环境热噪声基底大约为20dB［1］。面对日益复杂的电磁环境，干扰抑制处理的重要性日趋突出。

目前研究中常见的干扰抑制技术有时域，空域和空时域三大类。基于功率倒置(Power Inversion，PI)算法的自适应调零天线被证明是一种简单有效的空域滤波干扰抑制技术。该算法在不要求期望信号的波达方向等先验信息的情况下使天线阵列方向图在干扰入射方向形成零陷，而且干扰强度越大，对应零陷越深［2-3］。在不改变GPS接收机原有结构的前提下，将接收机天线更换为PI天线阵列系统，显著增强了接收机的抗干扰能力，易于工程实现。但是功率倒置算法对弱干扰进行抑制时，天线阵列方向图对应零陷深度不够，干扰抑制效果不理想。

本文以等距线阵为例，详细阐述了PI算法的基本原理，并且通过公式推导揭示了PI算法的本质，针对弱干扰抑制能力不足的缺点提出一种基于矩阵重构的PI改进算法。

1 PI算法［4］

PI阵列如图1所示。N为阵列阵元数目，阵元间距d=λ/2，λ为GPS信号L1载频所对应的波长(0.19m)。阵列的输入信号

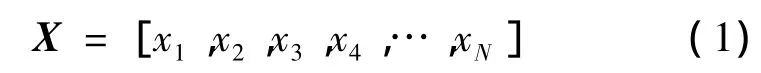
阵列自适应加权矢量

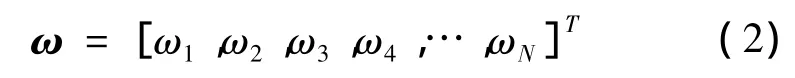
输出信号

输出信号功率

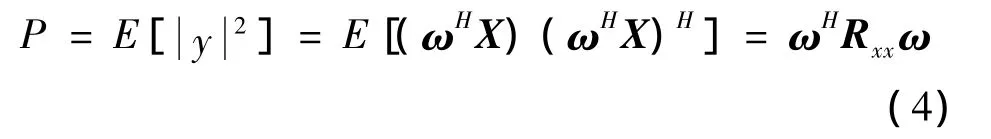
PI算法求得阵列权值矢量ω，使得输出信号功率P最小，即代价函数为:

式中Rxx为输入信号X的自相关矩阵。为了防止求得无意义解

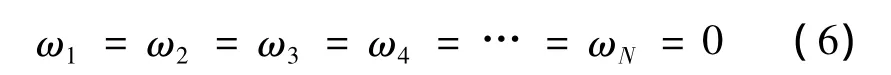
添加一个约束条件:第一个阵元上的加权值固定为1。

由拉格朗日函数求得最佳权值矢量为:

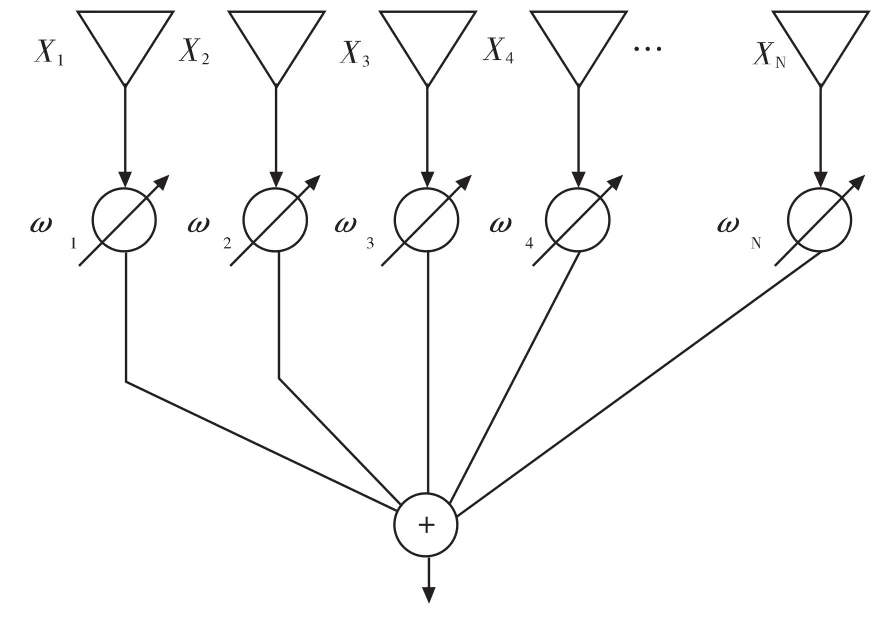
图1 功率倒置阵列示意图

约束条件保证第一阵元支路输出功率恒定，调整其他阵元加权值使得整个阵列输出功率最小，其物理意义在于PI算法不区分期望信号和干扰信号，只保证将阵列输出功率最小。通常干扰信号往往大大强于热噪声，而期望信号功率低于环境热噪声基底近20dB，所以PI算法对干扰信号的抑制要远远强于对期望信号的抑制。这种强信号大衰减，弱信号小衰减的过程提高了阵列的输出信号干扰噪声比，有利于后续的捕获跟踪和定位导航解算过程。

以8阵元的等距线阵为例，约定阵列法线方向为0°，顺时针方向为正角度方向，逆时针方向为负角度方向。有用信号使用L1载频的扩频信号，入射方向为0°;干扰信号为与GPS信号同载频的连续波干扰，入射角度为 45°，信号干扰功率比 SIR=-50dB;仿真中引入信号噪声功率比SNR=-20dB的高斯白噪声，各阵元通道噪声与干扰互不相关。仿真快拍数为2046，取1000次独立仿真平均结果。PI算法形成的阵列方向图如图2所示，在45°干扰入射方向形成深度约为-80dB的零陷，对干扰有很好的抑制效果。

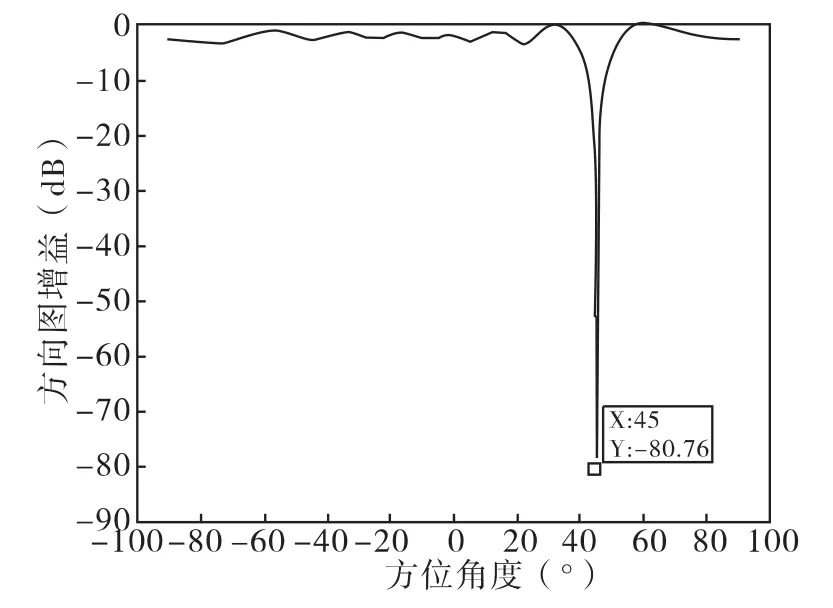
图2 PI算法8元阵方向图

图3为PI算法形成的零陷深度随输入干扰噪声功率比JNR变化曲线。由图3可以看出干扰强度越强，零陷深度越深。另外，输入JNR＜20dB时，PI算法阵列方向图在干扰方向上形成的零陷深度不够，导致干扰抑制效果不佳。

图3 零陷深度随输入JNR变化曲线

2 基于矩阵重构的PI改进算法

2.1 算法原理

对输入信号X的自相关矩阵Rxx进行特征值分解

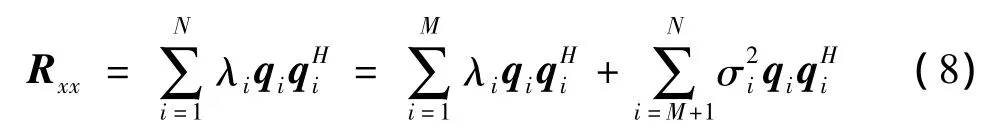
式中M为干扰信号个数，λi为Rxx的第i个特征值，qi为该特征值对应的特征向量，σi2为噪声功率。Rxx为N阶Hermite矩阵，不同特征值对应的特征向量相互正交，则有噪声特征向量与干扰特征向量正交。对Rxx求逆得

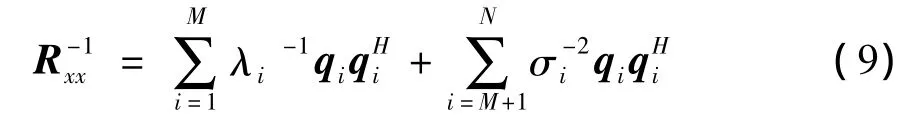
将(9)式代入(7)式可得

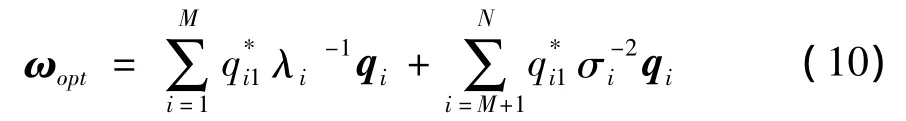
由(10)式可知，PI算法最优权值矢量为干扰特征向量和噪声特征向量的加权和，前一项为干扰信号特征向量加权和，后一项为噪声特征向量加权和。干扰特征向量与干扰信号导向矢量张成同一子空间，则干扰信号导向矢量为干扰信号特征向量的线性组合。强干扰环境下干扰特征值较大，对ωopt的影响反而小，可以认为ωopt位于噪声子空间，即ωopt是噪声特征向量的线性组合，因此ωopt与干扰信号导向矢量正交，在干扰方向上形成较深的零陷，而弱干扰环境下干扰特征值较小，与噪声特征值接近，对ωopt的影响反而大，因此在干扰方向上无法形成较深零陷［5］。增大弱干扰特征值可以减小ωopt中弱干扰特征向量的权重比例，从而加深在弱干扰方向上形成的零陷深度。接收信号自相关矩阵的特征值由两部分组成:前M个特征值等于干扰功率Pi与噪声功率σi2之和，后N-M个特征值全部等于噪声功率［6］。当JNR达到一定值时，干扰方向上零陷深度足够，此时接收信号自相关矩阵Rxx的干扰特征值与噪声特征值的比值为ρ。

基于矩阵重构的PI算法(以下简称改进算法)就是基于上述的分析，针对弱干扰源，先将接收信号自相关矩阵Rxx进行特征值分解，保持干扰特征向量、噪声特征值和噪声特征向量不变，增大干扰特征值，使其与噪声特征值比值保持ρ，然后重新构成新的接收信号自相关矩阵，最后根据(7)式求得阵列最优权值矢量ωopt。

2.2 算法仿真与分析

由图3可知，当输入干扰噪声功率比JNR为20dB，零陷深度大约为-60dB，干扰抑制效果良好，阵列输出信号干扰噪声功率比得到改善，此时干扰特征值与噪声特征值比值约为20dB。因此针对干扰噪声功率比JNR＜20dB的弱干扰，改进算法增大干扰特征值，使其与噪声特征值比值为20dB。

以8阵元的等距线阵为例，分析基于矩阵重构的PI改进算法的抗干扰性能。干扰噪声功率比JNR=0dB的干扰信号从45°入射，其余采用与上节中相同的仿真条件。

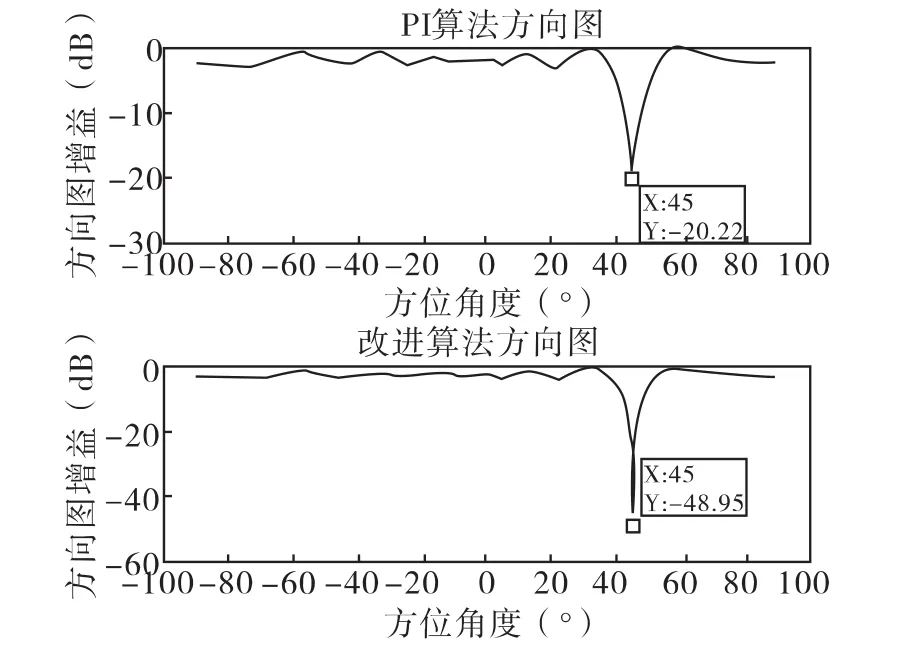
图4 PI算法和改进算法的方向图

图4分别示出JNR=0dB的干扰下PI算法和改进算法的方向图。可见，两种算法都准确地在干扰方向形成零陷，改进算法零陷深度加深约30dB，说明改进算法较PI算法有更强的弱干扰抑制能力。

图5示出两种算法在干扰方向零陷深度随输入JNR的变化情况。由图5可以看出，当JNR＜20dB时，改进算法零陷深度明显深于PI算法零陷深度，且两者零陷深度随着干扰噪声功率比JNR的增大而逐渐接近。

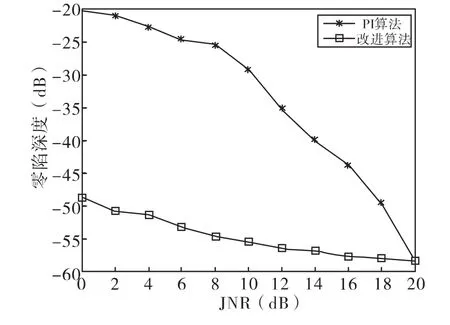
图5 零陷深度随输入SIR变化情况

对于多个干扰同时存在的情况，改进算法依然适用。先将接收信号自相关矩阵Rxx进行特征值分解，对各干扰特征值与噪声特征值比值进行判断，比值小于20dB则按照2．1节方法增大该干扰特征值，使比值增大到20dB;比值大于20dB则不做处理。此过程中保持干扰特征向量、噪声特征值和噪声特征向量不变，然后重构Rxx，通过(7)式求解最优权值矢量 ωopt。

假设干扰噪声功率比JNR=0dB的干扰信号J1从45°入射，干扰噪声功率比JNR=30dB的干扰信号J2从-45°入射，其余采用与上节中相同的仿真条件。

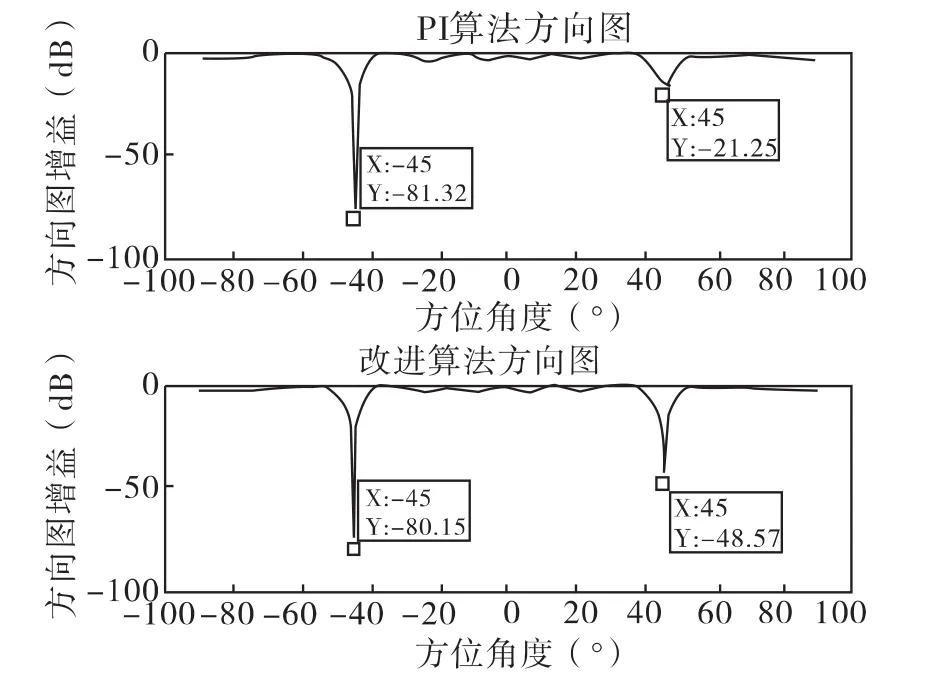
图6 PI算法和改进算法的方向图

图6中分别示出存在干扰信号J1和干扰信号J2情况下PI算法和改进算法的方向图。从图中可见，两种算法在干扰信号J2入射方向形成零陷基本相同，而干扰信号J1入射方向上，改进算法零陷深度比PI算法零陷大约有30dB的改善。由此可得，改进算法不仅适用于弱干扰存在的情况，也适用于强干扰和弱干扰同时存在的情况，比PI算法有更好的适应性。

3 结论

本文详细分析了PI算法的原理和干扰抑制性能，从公式推导的角度揭示PI算法针对弱干扰时零陷深度较浅的原因，并在此基础上并提出基于矩阵重构的PI改进算法。通过仿真实验证明了改进算法行之有效。本文算法不仅适用于GPS接收机，还可以应用在“北斗”二代等全球定位导航系统接收机。

［1］谢钢.GPS原理与接收机设计［M］.北京:电子工业出版社，2009.

［2］冯起，吕波，朱畅，袁乃昌.功率倒置自适应阵抗干扰特性研究［J］.微波学报，2009，25(3):87-91.

［3］何永前，李建璞.GPS抗干扰接收机自适应天线阵功率倒置算法研究［J］.舰船电子工程，2012，32(6):61-63.

［4］张文明.卫星导航系统干扰抑制技术［D］.长沙:国防科学技术大学，2002.

［5］王永良，丁前军，李荣峰.自适应阵列处理［M］。北京:清华大学出版社，2009.

［6］ 张贤达.现代信号处理［M］.第2版.北京:清华大学出版社，2002.