基于Ansoft软件的牵引用直线感应电机的有限元分析＊

李 霄 陶彩霞

（兰州交通大学自动化与电气工程学院，730070，兰州∥第一作者，硕士研究生）

城市的发展对新建城市轨道交通线路的制约条件越来越多，人们对轨道交通的要求也越来越高。直线感应电机轨道系统比传统感应电机轨道交通系统拥有更小的曲线半径、更强的爬坡能力，易在复杂的城市环境中运行，已成为多种城市轨道交通系统中的一员。广州地铁4号线、5号线和6号线，以及北京轨道交通首都国际机场线，都选择了这种城市轨道交通系统。然而，对于直线感应电机而言，存在道岔处感应板不连续、气隙值大、边端效应等问题［1－3］。本文利用 Ansoft软件的 Transient模块，采用有限元方法对直线感应电机在起动、稳态运行及经过道岔处的动态性能进行了分析。

1 牵引用直线感应电机的原理及特性

轨道交通一般采用短初级、复合感应板的单边型直线感应电机，其工作原理与旋转感应电机相同（如图1所示）。初级绕组被安装在列车底部，次级感应板铺设在轨道中心。由于初级绕组的开断，形成了两个边端。为了确保运行的安全，初级与次级感应极之间的间隙远远大于旋转电动机的气隙，因此体现出了多种特性。

图1 短初级单边型直线感应电机

直线感应电机不同于旋转感应电机的最大特点就是存在边端效应。边端效应可分为静态横向边端效应、动态横向边端效应、静态纵向边端效应和动态纵向边端效应。在直线感应电机轨道交通系统中，静态横向边端效应的本质是空载气隙磁场的横向扩散。当初级铁心叠片厚度小于次级感应板宽度时，这种效应对电机的影响往往可以忽略。动态横向边端效应与次级感应板横向超出初级绕组的长度和极距的比值相关：比值越大，动态横向边端效应对电机的影响就越小。通常比值大于0.4时，动态横向边端效应的影响会极大地削弱。增加电机的极数会减小互感之间的不对称。当极数增加到6以上时动态横向边端效应的影响可以忽略。纵向动态边端效应对牵引用直线感应电机的影响最大，需对其电磁特性进行分析，并在电机的设计和控制上进行完善。纵向动态边端效应所带来的影响是牵引用直线感应电机要解决的主要问题之一［1］。

2 直线感应电机的磁场基本方程

直线感应电机因其特有的边端效应，需利用麦克斯韦方程组计算其特性。麦克斯韦方程组需要作一些修改才能应用于直线感应电机。因为在交变磁场中导电媒质除因磁场随时间发生变化而产生感应电场外，还因磁场与导电媒质之间的相对运动而产生的速度电场。这两种电场在导电媒质中共同引起了感应电流。另外，直线感应电机的激励频率较低，所以位移电流可以忽略不计［4］。经过修改后，用于直线感应电机的基本电磁场方程为：

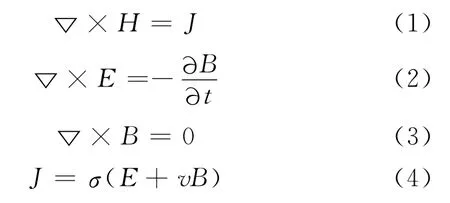
式中：

H——磁场强度；

E——电场强度；

B——磁感应强度（磁通密度）；

J——电流密度；

σ——电导率；

t——时间；

v——电荷在磁场中的运动速度。

为了估算磁场作用下所产生的力F，采用麦克斯韦应力张量是一种有效的方法。式（5）通过对一个包含初级绕组的封闭曲面进行面积分，来估算F

式中：

n——封闭曲面上的单位法向量；

B——磁感应强度矢量；

S——封闭曲面的面积。

那么磁场产生的推力和垂向力分别是力F的x和y向的分量，可分别表示为：

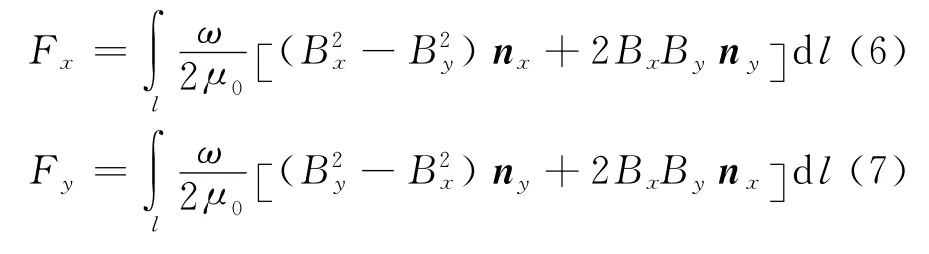
式中：

Bx——磁感应强度的x向分量；

By——磁感应强度的y向分量；

nx——封闭曲面上x向的单位正交矢量；

ny——封闭曲面上y向的单位正交矢量；

μ0——真空磁导率；

ω——初级铁心的宽度；

l——在二维分析中的围绕初级绕组区域的一条闭合线［5］。

3 牵引用直线感应电机的有限元仿真分析

3.1 有限元分析模型

通过Ansoft Maxwell 2D软件的Transient求解器，采用运动表面算法对做平移运动的直线感应电机进行瞬态仿真。忽略直线感应电机的横向边端效应，考虑道岔处感应板不连续的情况，对牵引用直线感应电机进行建模。电机主要参数见表1。

表1 牵引用直线感应电机主要参数表［6］

建模过程主要分为：生成几何模型，选定材料，设定激励源和边界条件，定义执行参数和定义求解选项［7］。其中，定义求解选项时需设置一个运动区域。该区域将运动的初级绕组和静止不动的次级感应板分开，做平移运动的初级绕组必须始终在运动区域中，并按照时间步长和速度值的设定做时步位移运动。为了使初级绕组在模拟运动中有足够的运动空间，运动区域要设置得足够长。物理模型如图2所示。对模型的气隙部分进行了细致剖分，以得到磁场产生的推力、垂向力和气隙磁场的精确计算结果。网络剖分如图3所示。

图2 直线感应电机物理模型图

图3 直线感应电机网络剖分图

3.2 动态性能分析

采用二维时步有限元分析法，通过后处理可以得到磁场产生的推力、垂向力、速度、位移及气隙中的磁通分布曲线［8］。

当直线感应电机空载运行、初速度为零、t＝0.01s时，磁力线分布如图4所示。从图中可以看出，磁通线由电机轭、电机齿进入空气隙后穿入次级感应板；再从另一个电机齿进入电机轭，形成一个极的闭合磁通线。由于电机两端存在半填充槽，利用率低，从而产生漏磁通。如图4所示电机含有6个极，其中5个完整的极和1个两端分开的极，两端磁通线通过空气闭合［9］。

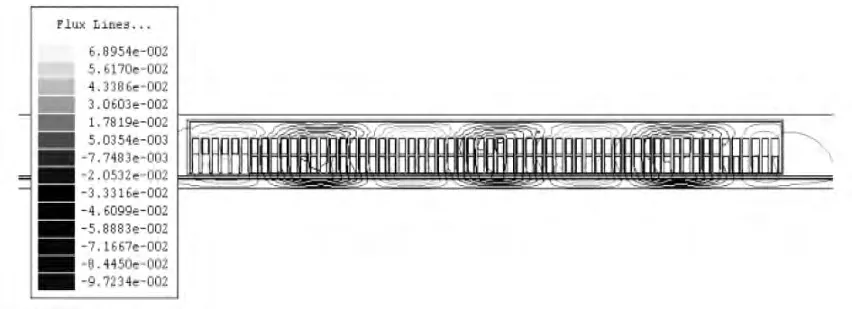
图4 直线感应电机磁力线分布仿真图（t＝0.01s）

图5～图8为不同时刻直线感应电机运行位置与气隙磁场密度分布图。t＝1.1s时，电机运行至图5－a）所示的位置，初级绕组的入端部分已和次级感应板脱离；此时气隙磁场密度分布如图5－b）所示，入端无次级感应板区域的气隙磁场分布相对平缓，没有电机极的体现，相当于电机极数减少，牵引能力随之减弱。t＝1.5s时，电机运行至图6－a）所示的位置，初级绕组和次级感应板完全脱离，气隙磁场密度分布如图6－b）所示；两者的电磁感应作用消失，磁通密度集中分布在同一区域。t＝2s时，电机运行至图7－a）所示的位置，初级绕组的入端部分驶出道岔，重新和次级感应板作用；此时气隙磁场密度分布如图7－b）所示，随着电机的继续运行，相当于极数随之增加，电机逐渐恢复正常运行状态。t＝2.3s时，电机运行至图8－a）所示的位置，次级感应板完全覆盖初级绕组；此时气隙磁场密度分布如图8－b）所示，可明显看到纵向边端效应的影响，而入端气隙磁场密度小于出端气隙磁场密度。

图9为直线感应电机的推力随时间变化的曲线。当电机为空载运行时，推力在初期处于震荡状态，0.52s后转为稳态，实际推力方向与软件中定义的推力方向相同，因此推力为正值；在0.78s后电机运动到感应板的边缘位置，进入无感应板的道岔区域，推力开始下降直到为零；当电机移出道岔重新和感应板相作用时，推力开始回升至稳态。图10为直线感应电机的垂向力随时间变化的曲线，其变化规律同推力曲线大致相同。稳态的垂向力为正值，表现为吸引力。当电机在道岔区域时垂向力为零，吸力消失，影响电机的稳定运行。

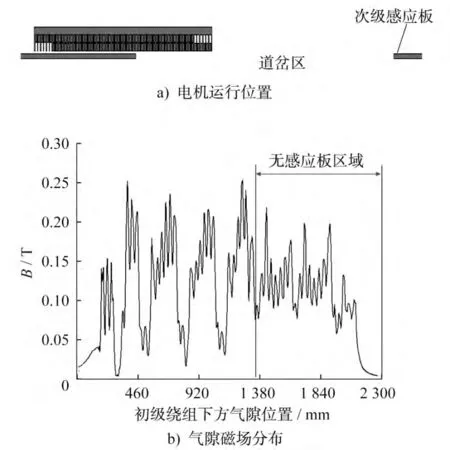
图5 直线感应电机运行位置与气隙磁场分布图（t＝1.1s）

图6 直线感应电机运行位置与气隙磁场分布图（t＝1.5s）

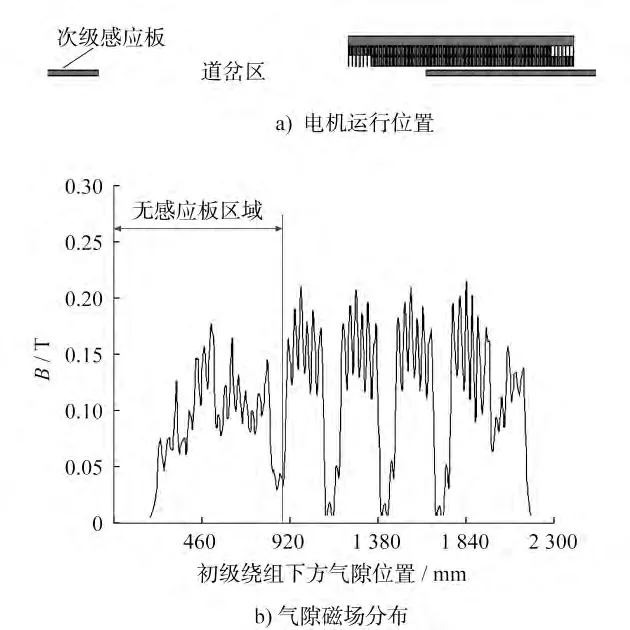
图7 电机运行位置与气隙磁场分布图（t＝2s）

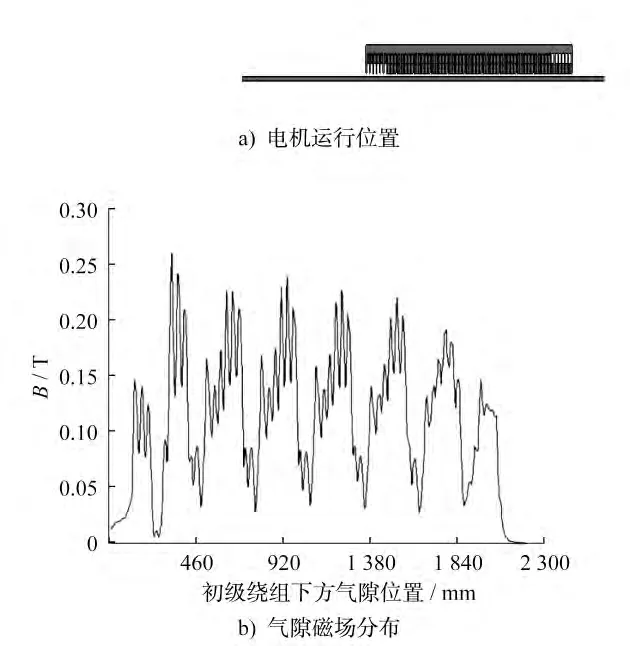
图8 电机运行位置与气隙磁场分布图（t＝2.3s）

4 结论

图9 直线感应电机的推力随时间变化曲线

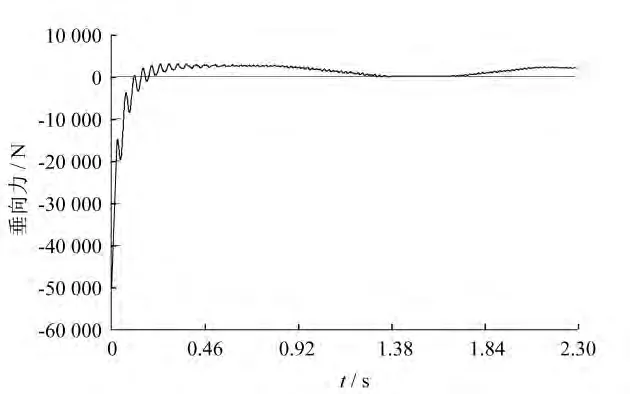
图10 直线感应电机的垂向力随时间变化曲线

本文简析了直线感应电机在轨道交通中的特性，运用有限元方法，忽略横向边端效应，并考虑道岔处感应板不连续的情况，建立了牵引用直线感应电机的二维瞬态电磁场模型；得到并分析了牵引用直线感应电机的磁力线、推力、垂向力和气隙磁场的特性曲线。仿真结果描述了直线感应电机运行至道岔区域时的变化规律，为牵引用直线感应电机的电磁设计与控制方法的优化提供了参考。

［1］郑琼林，赵佳，樊嘉峰.直线电机轨道交通牵引传动系统［M］.北京：中国科学技术出版社，2009：1.

［2］刘智成.直线电机运载技术在广州地铁的应用［J］.世界轨道交通，2005（3）：52.

［3］魏庆朝，蔡昌俊，龙许友.直线电机轨道交通概论［M］.北京：中国科学技术出版社，2009：8.

［4］龙遐令.直线感应电动机的理论和电磁设计方法［M］.北京：科学出版社，2006：22.

［5］Im Dal－Ho，Kim Chang－Eob.Finite element force calculation of a linear induction motor taking account of the movement［J］.IEEE Transactions on Magnetics，1994，30（5）：3495.

［6］Nonaka S，Higuchi T.Design of single－sided linear induction motors for urban transit［J］.IEEE Transactions on Vehicular Technology，1988，37（3）：167.

［7］赵博，张洪亮.ansoft12在工程电磁场中的应用［M］.北京：中国水利水电出版社.2010：130.

［8］郭明珠，方进，李永亮，等.基于ANSYS的高温超导直线感应电机仿真分析［J］.超导技术，2008，36（3）：23.

［9］裘昌利，张红梅，刘少克.基于Ansoft的直线感应电机性能分析［J］.微特电机，2006（12）：22.