稀疏微波成像研究进展(科普类)

吴一戎 洪 文 张冰尘 蒋成龙③ 张 柘③ 赵 曜

①(微波成像技术重点实验室 北京 100190)

②(中国科学院电子学研究所 北京 100190)

③(中国科学院大学 北京 100190)

1 引言

微波成像是一种不可或缺的遥感技术，它在农林监测、海洋监测、测绘制图、军事侦察等领域有着广泛的应用。现代高分辨率微波成像技术以合成孔径雷达(Synthetic Aperture Radar, SAR)为主，其特点为将雷达设备置于载机或卫星等运载平台上，运载平台相对于地面场景运动的同时，发射并接收电磁波。所获得的回波经过复杂的2维信号处理后，得到高分辨率的雷达图像。

SAR技术的出现始于上世纪50年代，由美国Goodyear公司的科学家Wiley提出，其在方位向利用合成孔径技术得到高分辨能力，因而得名合成孔径雷达。上世纪50年代到70年代是SAR系统发展的早期阶段，此间的SAR多为机载系统。1978年美国SEASAT发射，成为SAR发展史上的一个里程碑。SEASAT系统在典型模式下分辨率为25 m，测绘带宽为 100 km。其后数十年中，SAR技术在系统性能、应用范围等方面都得到长足发展，并具有极化SAR、干涉SAR、以及3维SAR等模式。1995年加拿大发射的 RadarSat-1系统在典型模式下分辨率为30 m，测绘带宽为100 km; 2007年德国发射的TerraSAR-X系统典型分辨率为3 m，测绘带宽则为30 km。随着SAR系统的发展，分辨率、测绘带宽等性能指标不断提升，其系统复杂度也不可避免地越来越高[1]。

回顾 SAR技术的发展史，两个基本因素决定了 SAR系统的性能：微波成像理论和电子学器件性能。微波成像理论在50年代就已出现，在随后的半个多世纪中，其理论虽不断完善，却没有出现革命性的创新。实际上，支撑SAR系统性能数十年的快速发展的，是在摩尔定律下飞速发展的电子学材料与器件。然而电子器件的性能提高不是无限的，摩尔定律虽然带来了电子产业数十年的繁荣，如今却面临瓶颈：由于量子效应的显现，人们在硅芯片性能的进一步提高上已经面临极限。此外，随着系统性能的提高而不断增加的雷达系统复杂度，也为SAR系统的设计和实现带来了越来越大的难度。但是，对高性能的SAR系统的需求却不会停止，面对着系统复杂度的瓶颈，另外的办法就是“另辟蹊径”在微波成像的理论上寻求突破[2]。

在微波成像理论中，雷达系统的复杂度由两个基本的理论决定：雷达分辨理论和奈奎斯特采样定理。根据雷达分辨理论，SAR系统分辨率上限由雷达信号的带宽决定。而根据奈奎斯特采样定理，系统的实采样频率必须至少为两倍的雷达信号带宽。这就是说，为了得到更高的SAR系统分辨率，就必须提高信号带宽，系统采样率也必须相应提高，这就意味着更高的数据率和更复杂的系统设计，从而使得SAR系统的设计与实现面临困难。无论是雷达分辨理论、还是奈奎斯特采样定理，都是普适性的理论，是不能违背的。唯一可行的办法，是从微波成像的特殊性入手，寄期望于微波成像的某些特殊性质可以突破传统雷达成像理论，建立新的微波成像理论并实现系统的简化。雷达场景和图像在很多情况下是具有明显稀疏性的，场景中只存在少数较强散射点，如图1所示。从数学角度看，这是一种典型的稀疏信号，即数学中描述大部分分量都是 0的信号。从上世纪90年代至今，数学中已经发展出了一套处理稀疏信号的理论，可以针对高维稀疏信号进行降维采样并实现稀疏重建。于是，利用一些典型雷达场景的稀疏性，将稀疏信号处理理论引入微波成像中，就成为了非常自然的思路。

稀疏信号处理理论至今仍在不断发展、完善中，是近年来数学界和工程界的一个研究热点，但是其基本思想却有着很久远的历史，可以追溯到古老的“奥卡姆剃刀”原理：若无必要，勿增实体。根据稀疏信号处理理论，若一个信号在某种变换域中是稀疏的，那么这个信号可以用一组数据量远小于原信号量的观测值加以描述。在稀疏信号处理领域的一个重要进展是由数学家 Donoho, Candes和 Tao等人提出的压缩感知(Compressive Sensing, CS)理论[3,4]。根据 CS理论，在采样系统满足某些要求的前提下，若信号是稀疏的，那么该信号可以由远低于奈奎斯特采样定理要求的采样率加以采样，并从采样值得到完美的重建。

图1 典型稀疏场景的雷达图像Fig.1 Typical sparse scene of SAR

稀疏微波成像是指将稀疏信号处理理论系统性地引入微波成像并有机结合形成的微波成像新理论、新体制和新方法[2]，即通过寻找被观测对象的稀疏表征域，在空间、时间、频谱或极化域稀疏采样获取被观测对象的稀疏微波信号，经信号处理和信息提取，获取被观测对象的空间位置、散射特征和运动特性等几何与物理特征。和传统的SAR相比，稀疏微波成像系统在降低数据率、降低系统复杂度并提升系统成像性能等方面有着潜在的优势，也是近年来微波成像理论界一个研究前沿与热点。

近年来，国内外有一批研究机构和科学家开展了将稀疏信号处理理论引入雷达成像的研究。Baraniuk等人首次提出可将压缩感知理论引入雷达成像中[5]。Potter等人研究了在雷达成像处理中采用稀疏重建算法以及随机采样策略[6]。Ender等人从现有雷达系统的框架出发，提出了基于压缩感知的雷达系统从理论到实用所面临的一些问题[7]。有关稀疏信号处理理论在SAR成像、目标检测以及3维成像等SAR应用中的研究也相应开展[8－11]。目前，从公开发表的文献中看，国外研究机构在相关领域尚未开展系统性研究。

国内，中国科学院电子学研究所、北京航空航天大学、西安电子科技大学、清华大学、国防科技大学、电子科技大学等单位开展了相关的研究工作。2010年，中国科学院电子学研究所在国家重点基础研究计划(973计划)的支持下，联合国内优势单位组织开展“稀疏微波成像的理论、体制和方法研究”项目。该项目围绕微波成像稀疏表征与变换域映射、微波成像稀疏观测约束、稀疏微波成像非模糊重建等难点问题，研究稀疏微波成像的基础理论、数据获取、信号处理、数据压缩与特征理解等内容，在稀疏微波成像系统的概念和理论框架、体制、算法、原理性验证方面取得原创性成果。在此基础上，构建基于航空和地面平台的稀疏微波成像实验验证系统，获取稀疏微波成像体制雷达的实验数据，完成稀疏微波成像的原理性验证。

2 关键科学问题

稀疏信号处理是本世纪信号处理领域最活跃的分支之一。该分支的研究目标是从原始信号中提取尽可能少的观测数据，同时最大限度地保留原始信号中所含信息，对原始信号进行有效的逼近和恢复。压缩感知是稀疏信号处理近年来一个重要的理论突破，它的本质是求解欠定方程的问题(如图2所示)。一般来讲，方程中未知数的个数大于方程的个数，方程有无穷多个解。然而根据压缩感知理论，当方程解的非零元个数很少，也就是说，方程解具有稀疏特性，并且方程组满足某种条件时，方程可以利用稀疏重构方法求解[3,4]。

稀疏微波成像数据采集过程可以用一个线性系统的传递函数表示，可以将回波采样数据用观测对象数据线性表出，即

其中，Y为回波采样数据，X为稀疏微波观测对象，这里Y的维数小于X的维数，H为微波成像系统观测矩阵，N为系统观测噪声。如图3所示，成像过程即是通过正则化算法[12]等稀疏重构方法利用回波采样数据Y对X进行估计。

将稀疏信号处理引入微波成像中主要存在以下难点[2]：

(1) 微波成像稀疏表征与变换域映射

稀疏微波成像要求观测对象具有稀疏特性，或者存在一个由稀疏基构成的稀疏变换矩阵，使得地面场景在该矩阵下的系数为稀疏向量。微波成像所观测的对象，通常是地面场景或目标，它们本身往往具有较强的相关性，即存在信息冗余，所以具有稀疏性。稀疏微波成像表征与变换域映射针对稀疏度不同的观测场景，寻找相应的稀疏变换矩阵，使被观测对象在此稀疏基张成的空间中可稀疏表征，建立一般性稀疏表征规律和映射关系。

(2) 微波成像稀疏观测约束

图2 稀疏信号处理观测模型Fig.2 Measurement model of sparse signal processing

图3 稀疏微波成像模型示意图[2]Fig.3 Diagram of sparse microwave imaging model, figure cited from Ref.[2]

微波成像过程是在对回波数据进行相干积累的基础上，恢复出被观测对象的微波图像，其稀疏微波成像系统观测矩阵由稀疏矩阵和微波成像系统观测矩阵共同决定。因此，稀疏微波成像系统观测矩阵的构建必须考虑成像雷达观测系统及其约束条件。为实现稀疏微波成像，必须在微波成像的稀疏观测约束条件的基础上，利用其在空间、时间、频谱、极化、或者多维度联合稀疏特性，研究基于稀疏微波成像系统观测矩阵的数据获取方法。

(3) 稀疏微波成像非模糊重建

稀疏微波成像非模糊重建需要在建立稀疏成像算子的同时，建立全采样微波成像算子和稀疏成像算子的对应关系。由于观测过程的线性降维，使得稀疏成像算子的构建存在困难，属于“不适定”问题。同时，微波成像系统误差、回波散射调制、噪声等引起稀疏微波成像系统观测过程的模型偏差，需解决这些因素对算法稳健性的影响。此外，微波成像中海量数据获取、凸优化高维迭代带来的大尺度稀疏微波成像优化问题数值求解难题。

另外，稀疏微波成像的性能评估也是一个难点。需要结合稀疏微波成像的特点，研究能有效衡量稀疏化成像质量的方法，实现对稀疏微波成像定量分析和评估。

3 稀疏微波成像主要研究进展

稀疏成像的研究结果表明：利用稀疏微波成像的信号处理方法可应用于现有雷达数据并提高其图像质量；利用稀疏微波成像的工作原理可以设计性能更优的成像雷系统；另外，利用分布式压缩感知技术可以进一步降低多通道雷达的数据量及系统复杂度。

(1) 稀疏微波成像信号处理方法应用于现有雷达数据并提高其图像质量。

中国科学院电子学研究所提出直接从原始数据域进行稀疏微波成像框架，如图 4(a)所示，直接从原始数据域进行稀疏微波成像可以对满/降采样的雷达回波数据进行非模糊重建，才能真正降低微波成像系统的复杂度。而基于距离向压缩后数据域的压缩感知成像方法，如图4(b)所示，需要对满采样的雷达回波数据进行预处理，如距离压缩、距离徙动校正等，两维解耦后再进行重建，增加了系统复杂度。

直接从原始数据域利用稀疏微波成像算法进行场景重建面临计算量大的困难。针对该问题提出了基于回波模拟算子的稀疏微波成像算法快速实现[13,14]。该算法对回波数据进行 2维解耦，使计算效率由提高至，其计算量与现有雷达成像算法计算量相当，从而使稀疏微波成像算法应用于现有雷达数据处理成为可能。

利用稀疏微波成像算法不但可以在降采样的条件下重建稀疏目标场景，如图5所示，也可以在满采样的条件下重建非稀疏目标场景，如图6所示。与传统基于匹配滤波算法的成像结果相比，抑制了强目标的旁瓣，改善了目标的分辨能力，提高图像质量。

利用稀疏微波成像算法还可以解决传统成像中不可避免的模糊问题，减少虚假目标出现概率，有助于雷达图像的目标解译。该方法是通过结合天线方向图信息构造观测模型，并且利用稀疏微波重构算法实现对目标场景的模糊抑制成像，如图7所示。

(2) 稀疏微波成像原理设计性能更优的成像雷系统

海洋目标观测是稀疏微波成像应用的一个典型例子，海面场景目标可认为具备稀疏特性，在这种条件下，利用稀疏微波成像原理可以设计更高分辨能力和更宽测绘带宽的雷达系统，以满足应用需求。

(3) 分布式压缩感知技术进一步降低多通道雷达的数据量及系统复杂度。

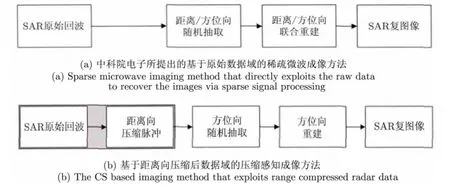
图4 稀疏微波成像方法流程示意图Fig.4 Flowcharts of the sparse microwave imaging methods

图5 典型舰船目标的不同成像方法结果对比图[2]，原始数据来自于RadarSat-1[17]Fig.5 Reconstruction of a typical sparse scene based on RadarSat-1 data[17], figure cited from Ref.[2]

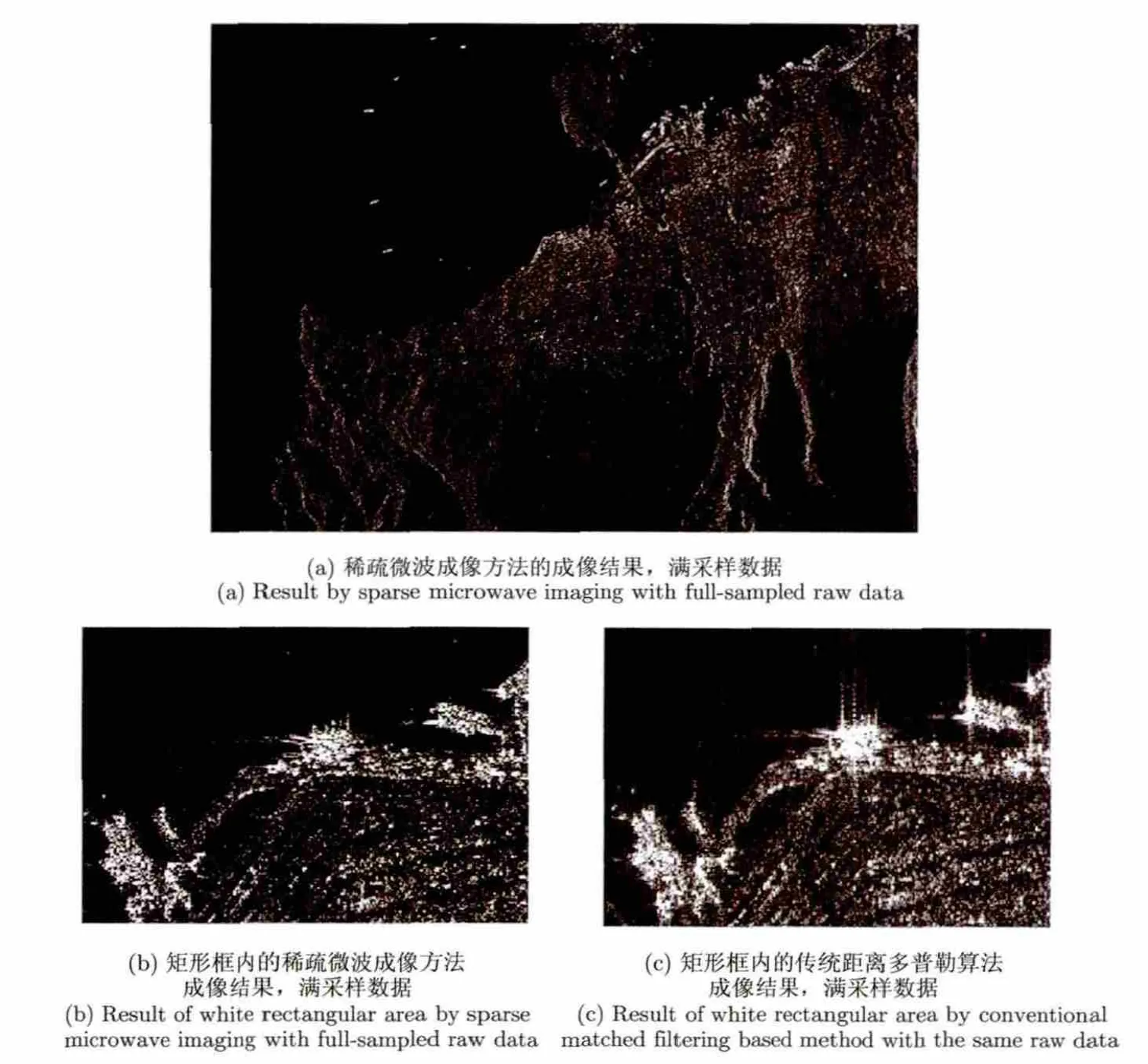
图6 典型复杂场景的不同成像方法结果对比示意图[2]，原始数据来自于RadarSat-1[17]Fig.6 Reconstruction of a typical non-sparse scene based on RadarSat-1 data[17], figure cited from Ref.[2]

分布式压缩感知技术可应用于存在信息冗余的多通道雷达系统，如多通道运动目标检测，目标变化检测等。在场景变化检测中，多次观测的数据等效形成多通道信号，若场景变化较少，则通道间信号的更新分量就是稀疏的，利用分布式压缩感知可以采集更少的数据实现场景重建和目标变化检测[15]。在顺轨干涉运动目标检测中，若运动目标作为更新分量是稀疏的，则分布式压缩感知运动目标检测技术能够利用更少的采样数，获得与满采样传统技术相同的结果[16]。中科院电子所地基实验平台基于稀疏微波成像的场景变化检测实验结果表明，在同样降采样比的条件下，利用分布式压缩感知技术可以获得更好的变化检测效果，如图8所示。

4 稀疏微波成像机载飞行实验

稀疏微波成像机载实验验证的主要内容包括两个部分。一是设计和研制稀疏微波成像机载原理样机；二是开展机载飞行实验，通过实验结果验证稀疏微波成像在数据获取体制、信号处理方法等方面的可行性。

4.1 机载原理样机设计

图7 稀疏微波成像方位模糊抑制示意图[2]Fig.7 Numerical simulation of ambiguity suppression by the sparse microwave imaging method on point target with full under-sampled data, figure cited from Ref.[2]

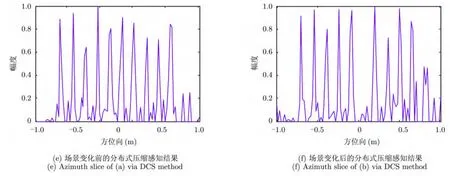
图8 基于稀疏微波成像的场景变化检测示意图[15]，45%降采样数据，原始数据来自中科院电子所地基实验平台Fig.8 Results of multi-temporal scene change detection experiment with 45%under-sampled raw data of IECAS GBSAR, figure cited from Ref.[15]

稀疏微波成像雷达原理样机的设计重点在于稀疏采样的设计，同时需要考虑信噪比等系统雷达参数[2,18]。在观测目标可被稀疏表征的情况下，稀疏微波成像雷达可以使用比传统系统更少的数据。为达到优化的系统性能，在原理样机的设计中稀疏采样策略采用了“抖动采样”方式，如图9所示。在降采样的同时，限制系统瞬时脉冲重复间隔，从而保证系统测绘带宽的要求。

稀疏微波成像系统的性能相变图可以用相变图来综合分析和评估稀疏微波成像系统的性能，为稀疏微波成像雷达原理样机提供设计工具[2]。相变图来源于物理学中的热力学，稀疏微波成像中的相变图是3维的，具有稀疏度、欠采样比、信噪比3个变量轴，如图10所示。借用相变边界曲线来精细刻画稀疏微波成像雷达中稀疏度、采样比、信噪比与准确重建概率的等价性条件分析稀疏微波成像雷达性能。

4.2 飞行实验验证

2013年9月，中国科学院电子学研究所在天津滨海地区开展了稀疏微波成像原理样机的飞行试验。通过该实验验证了稀疏微波成像原理和方法的可行性，并针对典型稀疏场景(如图11所示)验证了利用相变图评估系统信噪比、降采样等参数设计准则的有效性。在相同的降采样率下，非均匀采样的性能高于均匀采样，如图12所示；在相同的采样方式下，降采样程度越高，成像效果越差，如图13所示，这也符合人们的直观判断。

该飞行实验系首次开展系统性的稀疏微波成像雷达可行性验证，重点评估了参数设计准则的有效性，实验结果达到了预期目的，为稀疏微波成像雷达系统的后续研制工作奠定基础。

5 稀疏微波成像相关应用

近年来，国内外单位对稀疏信号处理在雷达相关技术中的应用开展了广泛的研究，研究领域包括：3维 SAR、逆 SAR、探地/穿墙雷达、宽角/圆迹SAR、动目标检测、MIMO雷达等。

(1) 3维SAR

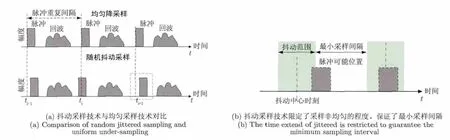
图9 随机抖动采样方式示意图Fig.9 Illustration of random jittered sampling

3维 SAR (3D-SAR)，也被称为层析 SAR(Tomographic SAR, TomoSAR)，它将传统的2维成像SAR扩展到了3维。在实际3维SAR应用中，其高程维分辨率远低于另外两个维度的分辨率，影响了3维图像效果。由于目标散射特性在高程维是稀疏的，因此稀疏信号处理理论可应用于高程向的超分辨成像。目前，国内外研究机构将这种超分辨成像方法成功应用在 TerraSAR-X[8], COSMOSkyMed[19], ERS1/2, GOTCHA和地基等数据集上。图14所示的是利用稀疏信号处理获得的星载SAR层析成像结果。

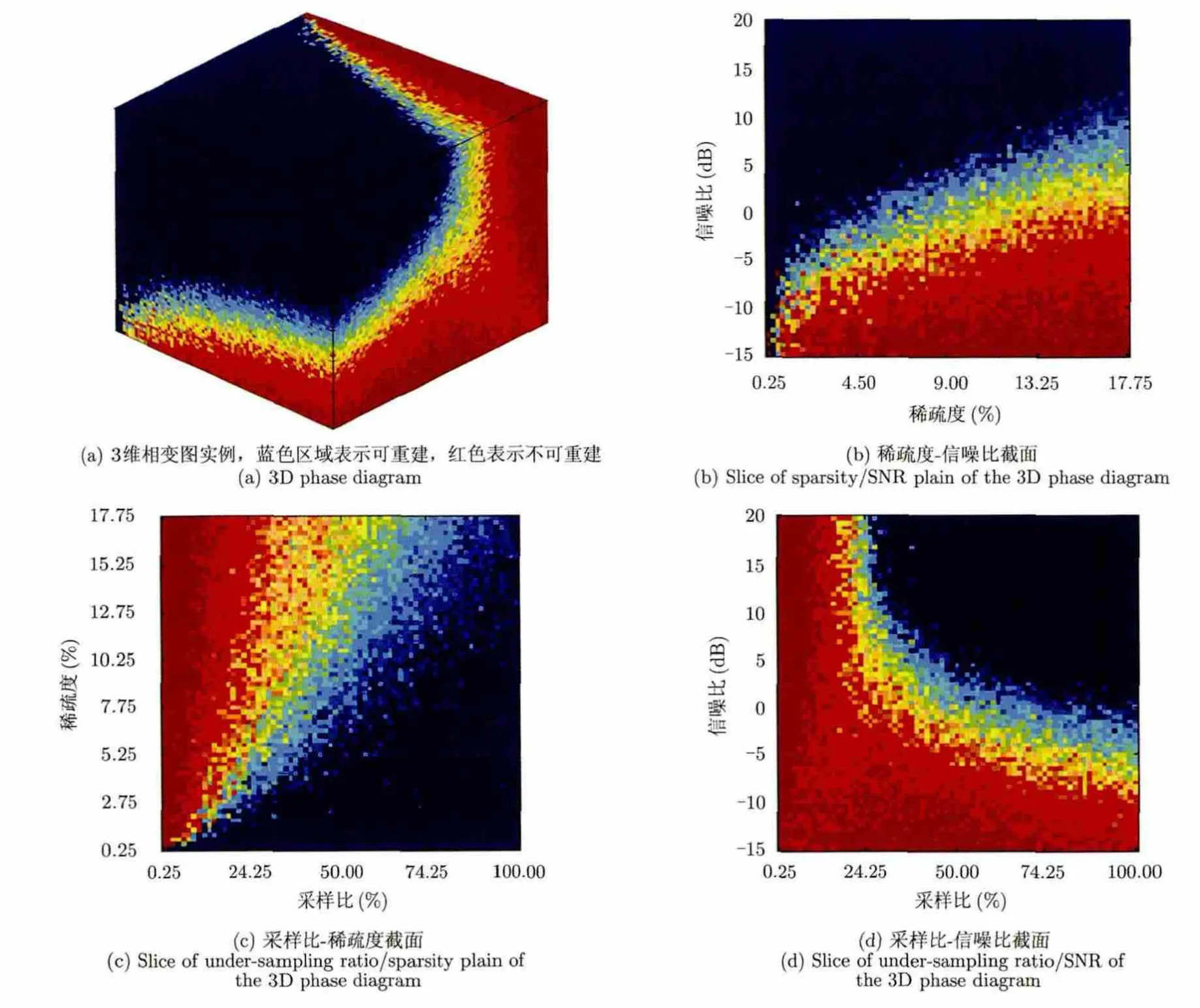
图10 稀疏微波成像雷达相变图示意图Fig.10 A 3D phase diagram and 2D slices.The colors of points in the 3D phase diagram exhibit the success rates for each combination,where red means the recovery fails, deep blue means the recovery succeeds, figure cited from Ref.[2]

图11 盐田光学图像，图像来源于谷歌地球Fig.11 Optical images of salt pan, copyright by google earth

图12 典型稀疏目标稀疏微波成像结果，验证不同采样方式，稀疏度约4.5%，采样比60%Fig.12 Imaging results and phase transit diagram of different sampling schemes, with 4.5% sparsity and 60% under-sampling rate Green circle is the point that represents the experiment condition

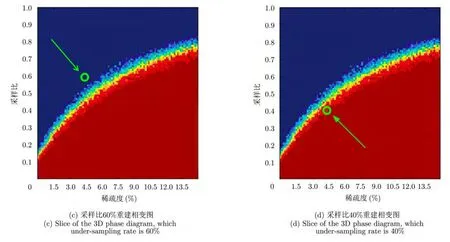
图13 典型稀疏目标稀疏微波成像结果，验证不同采样比，稀疏度约4.5%，随机抖动采样Fig.13 Imaging results and phase transit diagram of different under-sampling rate, with 4.5% sparsity, non-uniform sampling Green circle is the point that represents the experiment condition

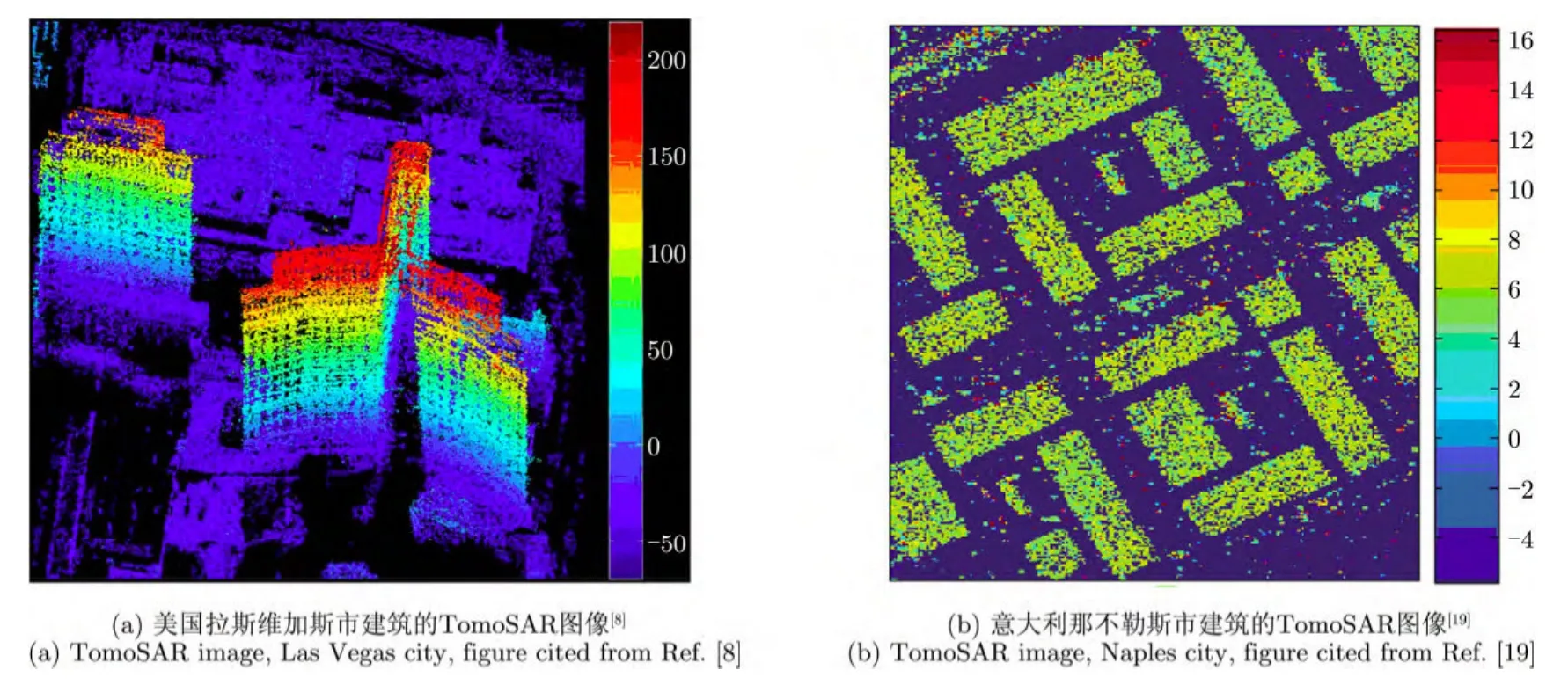
图14 TomoSAR稀疏成像结果Fig.14 Illustrations of imaging results of TomoSAR

(2) 逆SAR

逆SAR(Inverse SAR, ISAR)在观测过程中，雷达平台固定，而被观测的目标运动，它常用于观测天空目标如飞机、海洋目标如舰船等。这些目标相对于背景具有天然的稀疏性，因此稀疏信号处理理论可以很自然地应用于ISAR成像[7,20]，图15所示的是实测数据成像结果。

(3) 探地/穿墙雷达

探地雷达(Ground Penetrating Radar, GPR)是一种地下目标高分辨率无损伤探测技术，主要用于检测并定位地球表面下或一个不透明实体内的目标或介面。在地下目标稀疏的条件下，可以将稀疏信号处理理论引入到探地雷达成像，且可抑制杂波。穿墙雷达(Through-the-Wall Radar Imaging,TWRI)在原理上和探地雷达颇为接近，因此稀疏信号处理理论同样可应用于该领域[9,21]，图 16(a)和图16(b)所示的分别是探地雷达和穿墙雷达的成像结果。

(4) 宽角/圆迹SAR

宽角SAR (Wide Angle SAR, WASAR)是指在数据采集过程中雷达在方位向跨越一个很宽的角度范围，以获得更高的方位向分辨率以及更多的目标方位角散射信息。由于实际目标后向散射系数通常是各向异性的，传统的SAR成像方法并不适合对宽角 SAR进行成像。稀疏微波成像理论可以为这一问题提供解决思路[22]。作为宽角SAR的一种变形，圆迹SAR(Circular SAR, CSAR)的雷达平台相对观测目标作圆周运动，雷达波束始终照射目标场景区域，从而形成目标的2维孔径，实现对目标的3维观测。圆迹SAR也可以结合稀疏信号处理方法进行成像[10]，图 17(a)和图 17(b)所示的分别是宽角SAR和圆迹SAR的成像结果。

(5) 动目标检测

动目标检测是一种区分运动目标和静止背景的一种雷达模式。运动目标在速度/位置域具有稀疏性。因而稀疏微波成像也适用于这个领域[11,23]，图18(a)和图18(b)分别是实测以及仿真数据的成像结果。

(6) MIMO雷达

多输入多输出雷达(Multiple Input Multiple Output Radar, MIMO Radar)是指雷达通过多个发射天线发射相互正交的信号，并由多个接收天线同时接收回波信号。由于相互独立回波能够增加雷达的接收增益，MIMO技术被用到雷达中用来增加雷达的分辨力与目标识别能力。当目标满足稀疏性时，压缩感知技术也可以被应用到MIMO雷达中。

6 展望

稀疏微波成像作为微波成像中的新概念和新体制，在遥感应用中已经取得了重要的进展。目前稀疏微波成像仍在不断发展完善中，亟待解决在误差理论分析、观测矩阵优化等方面的技术难题。随着稀疏信号处理理论和方法的逐步完善，稀疏微波成像将逐步走向实用化和工程化，将在宽幅海洋稀疏目标雷达成像、3维SAR、逆SAR、被动雷达目标探测、运动目标检测、探地/穿墙雷达、宽角/圆迹 SAR、特征提取、数据压缩等相关领域获得巨大的应用。

图15 ISAR稀疏成像结果Fig.15 Illustrations of imaging results of ISAR

图17 宽角SAR和圆迹SAR稀疏成像结果Fig.17 Illustrations of imaging results of WASAR and CSAR

图18 动目标稀疏成像结果示意图Fig.18 Illustrations of imaging results of moving targets

[1]Curlander John C and Robert N McDonough.Synthetic Aperture Radar[M].New York: John Wiley & Sons, 1991.

[2]Zhang Bing-chen, Hong Wen, and Wu Yi-rong.Sparse microwave imaging: Principles and applications[J].SCIENCE CHINA Information Sciences, 2012, 55(8): 1722-1754.

[3]Donoho D L.Compressed sensing[J].IEEE Transactions on Information Theory, 2006, 52(4): 1289-1306.

[4]Candes E J and Tao T.Near-optimal signal recovery from random projections: universal encoding strategies?[J].IEEE Transactions on Information Theory, 2006, 52(12):5406-5425.

[5]Baraniuk R and Steeghs P.Compressive radar imaging[C].2007 IEEE Radar Conference, 2007: 128-133.

[6]Potter L C, Ertin E, Parker J T, et al..Sparsity and compressed sensing in radar imaging[J].Proceedings of the IEEE, 2010, 98(6): 1006-1020.

[7]Joachim H G Ender.On compressive sensing applied to radar[J].Signal Processing, 2010, 90(5): 1402-1414.

[8]Zhu Xiao-xiang and Bamler R.Demonstration of super-resolution for tomographic SAR imaging in urban environment[J].IEEE Transactions on Geoscience and Remote Sensing, 2012, 50(8): 3150-3157.

[9]Gurbuz A C, McClellan J H, and Scott W R.A compressive sensing data acquisition and imaging method for stepped frequency GPRs[J].IEEE Transactions on Signal Processing,2009, 57(7): 2640-2650.

[10]Austin Christian Ertin D E, and Moses R L.Sparse signal methods for 3-D radar imaging[J].IEE E Journal of Selected Topics in Signal Processing, 2011, 5(3): 408-423.

[11]Prunte L.GMTI from multichannel SAR images using compressed sensing[C].9th European Conference on Synthetic Aperture Radar, 2012, EUSAR, 2012: 199-202.

[12]XU Zong-ben, GUO Hai-liang, WANG Yao, et al..Representative of L1/2Regularization among Lq(0

[13]Fang Jian, Xu Zong-ben, Zhang Bing-chen, et al..Fast compressed sensing SAR imaging based on approximated observation[J].IEEE Selected Topics in Applied Earth Observations and Remote Sensing, 2014, 7(1): 352-363.

[14]Jiang C L, Zhang B C, Fang J, et al..Efficient ℓqregularisation algorithm with range-azimuth decoupled for SAR imaging[J].Electronics Letters, 2014, 50(3): 204-205.

[15]Lin Yue-guan, Zhang Bing-chen, Jiang Hai, et al..Multichannel SAR imaging based on distributed compressive sensing[J].SCIENCE CHINA Information Sciences, 2012,55(2): 245-259.

[16]Lin Y G, Zhang B C, Hong W, et al..Along-track interferometric SAR imaging based on distributed compressedsensing[J].Electronics Letters, 2010, 46(12): 858-860.

[17]Cumming I G, and Wong F H.Digital Processing of Synthetic Aperture Radar Data: Algorithms and Implementation[M].Boston: Artech House, 2005.

[18]Hong Wen, Zhang Bing-chen, Zhang Zhe, et al..Radar imaging with sparse constraint: principle and initial experiment[C].Processings of 10th European Conference on Synthetic Aperture Radar, EUSAR 2014, Berlin, Germany.

[19]Domenico B, Budillon A, and Schirinzi G.Compressive sampling in SAR tomography: Results on COSMO-skymed data[C].2012 IEEE International Conference in Geoscience and Remote Sensing Symposium (IGARSS), 2012: 475-478.

[20]Zhang Lei, Qiao Zhi-jun, Xing Meng-dao, et al..Highresolution ISAR imaging by exploiting sparse apertures[J].IEE E Transactions on Antennas and Propagation, 2012, 60(2): 997-1008.

[21]屈乐乐, 方广有, 杨天虹.压缩感知理论在频率步进探地雷达偏移成像中的应用[J].电子与信息学报, 2011, 33(1): 21-26.Qu Le-le, Fang Guang-you, and Yang Tian-hong.The application of compressed sensing to stepped-frequency ground penetrating radar migration imaging[J].Journal of Electronics & Information Technology, 2011, 33(1): 21-26.

[22]Moses R L, Potter L C, and Cetin M.Wide-angle SAR imaging[C].Conference on Algorithms for Syntheic Aperature Radar Imagery Ⅺ, Bellingham, 2004: 164-175.

[23]马泽强, 王希勤, 刘一民, 等.基于稀疏恢复的空时二维自适应处理技术研究现状[J].雷达学报, 2014, 3(2): 217-228.Ma Ze-qiang, Wang Xi-qin, Liu Yi-min, et al..An overview on sparse recovery-based STAP[J].Journal of Radars, 2014, 3(2):217-228.