基于效用函数的装备保障效能评估方法
王琴琴,宋太亮,汤伟达,赵潇逸
(1.装甲兵工程学院,北京 100072;2.解放军72726部队,济南 250023;3.中国国防科技信息中心,北京 100072;4.烟台警备区保障部,山东 烟台 264000;5.装备学院,北京 101416)
基于效用函数的装备保障效能评估方法
王琴琴1,2,宋太亮3,汤伟达4,赵潇逸5
(1.装甲兵工程学院,北京 100072;2.解放军72726部队,济南 250023;3.中国国防科技信息中心,北京 100072;4.烟台警备区保障部,山东 烟台 264000;5.装备学院,北京 101416)
论述了保障效能及其评估的内涵,按照能力-性能-特性的思路,建立了科学合理的装备保障效能评估指标体系,给出了定量定性指标构建效用函数的方法,建立出装备保障效能评估的数学模型,并应用具体实例进行了验证。
装备保障,效用函数,效能评估
引言
装备在完成某一具体作战任务时的能力,称为任务效能,从保障角度讲,可以称为执行该项任务的保障效能。保障效能描述了一定条件下,装备系统被用来完成保障任务所能达到预期目标的程度[1]。保障效能的评估通常采用建模仿真的方法,然而这种仿真的可信度主要依靠建模的准确度,目前的建模技术下,人机交互以及交互带来的复杂变化无法准确建模,因此,这种仿真推演方法不具备实际应用基础。
与其他综合评估方法相比较,效用函数评估法的最大优点是:评估模型既具有主观性又具有客观性,且评估结论具有直观性和通俗性。特别是评估过程中各环节之间没有信息传递,而且每个环节都有许多的方法可供选择和组合[2]。因此,本文给出了不同指标效用函数的构造方法,建立了装备保障效能评估模型。
1 保障效能评估总体思路
保障是为作战服务的,保障效能的好坏是在执行任务的整个过程中体现出来的。因此,要想评估保障效能,首先应对所执行的任务需求进行分析,按照任务前、任务中、任务后,以时序将作战使用流程和工作内容描述清楚。其次,根据作战任务要求,分析为完成任务的每个阶段所需要的保障能力要求,涉及所需装备总数、人员配备及训练方案情况、备件及消耗品、保障设备等物资资源、保障程序和方法,以及保障指挥及信息保证情况等方面。
通常对保障能力可以提出以下几类要求:
(1)接到任务后能够快速出动的能力;
(2)执行任务过程中能够持续执行任务的能力;
(3)执行任务过程中装备故障或战损后能够得快速修复的能力;
(4)接到新任务或任务转场时能够具有快速重新部署的能力;
(5)执行任务过程中信息获取分发及时准确的能力。
这些能力对不同的装备有所不同,对同一装备执行不同的任务也有所不同。这个时候的保障能力要求是目标性的且比较粗略的,还需要进一步分解和细化成保障性能要求,保障性能要求进一步分解成保障特性要求,其中保障特性要求包括保障性设计要求及保障资源要求,经过层层分解,最终形成具体、好理解、可操作的评估指标体系。具体过程如图1所示。

图1 能力-性能-特性指标映射模型
为了计算出装备的总体保障效能(TSE),需要根据每一保障特性指标的重要程度,确定每一保障特性指标的权重,通过效能值乘以权重逐层累加,就可以计算装备的总体保障效能。由于每个特性有不同的量纲,需要采用特性指标的效用函数(效用函数表征了特性指标与效能值之间的映射关系)。对每一项特性指标画出效用函数曲线,0.6对应的是特性指标的门限值,1对应的是特性指标的目标值,通过建立特性指标与效能的映射关系,用特性指标实际达到的数值计算其效能值,这样也可以解决特性指标数值量纲不一致的情况。
2 基于效用函数的保障效能评估方法
2.1 保障效能评估指标体系的建立和权重的确定
根据装备保障效能的实际情况,按照能力-性能-特性的思路,层层分解细化,确定对应的指标,并且采用德尔菲法确定各指标的权重,形成如图2所示的指标体系。

图2 保障效能评估指标体系及权重
2.2 单指标效用函数构建
评价指标分为定量指标和定性指标,在单指标效用函数的构建中,对于不同的指标,采用不同的构建方法。
2.2.1 定量指标效用函数
在装备保障效能评估中,根据定量指标的性质,将效用函数大致分为两类:极大值型和极小值型效用函数。极大值型效用函数曲线通常有5种典型形状,如图2中的曲线A、B、C、D、E极小值型效用函数曲线通常也有5种。效用函数表征了指标值与效能值之间的映射关系。其中,效能值与具体任务相关,由(0~1.0)之间的单一数值进行表示。如图3所示。

图3 定量指标效用函数图
(1)绘制效用函数曲线
对于定量指标,规定其门限值对应效能值为0.6,目标值对应效能值为1.0,当指标值大于目标值时,对应效用值为1.0,当指标值小于门限值时,对于规范有最低要求的指标或部分关键性指标效用值取0,其他指标可在0~0.6之间取值。
令门限值为x1,目标值为x3,则u(x1)=0.6,u(x3)=1.0,为了测定基准效用值,各以0.5的概率取门限值x1和目标值x3,构成简单事态体,并用标准效用测定法[3],得到事态体的确定当量x2,使得:
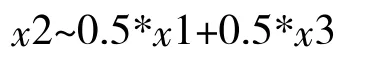
即以1的概率取x2的效用和以0.5的概率取门限值及目标值的效用是一样的。则由效用函数的定义可知:
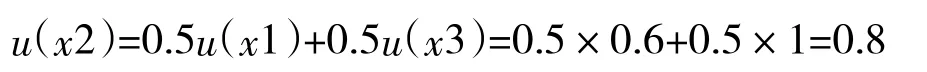
于是,就得到效用函数曲线上的3个点(x1,0.6)(x2,0.8)(x3,1.0)。
按照同样的思路,各以0.5的概率取x1和x2,得到一个新的当量x4使

于是又得到效用函数上的一个点(x4,0.7),以此类推,得到效用函数曲线上的其他点,根据得到的这些散点,大致绘出效用函数曲线的形状。
(2)拟合效用函数曲线
根据效用函数曲线的形状,选择合适的多项式回归方法进行曲线拟合。例如,如果曲线形状为A、E、F、J形,则可选择二次或三次多项式进行拟合,S形曲线则可以选择三次或三次以上的多项式进行拟合。本文中利用MATLAB,直接调用命令polyfit(x,y,n)实现最小二乘多项式曲线拟合。对于拟合后的曲线采用重点数据法进行检验,即给出另外一个或一组数据,代入拟合的曲线,计算其误差,如果误差在合理范围内,则接受拟合的曲线;如果误差过大,则采用更高阶次的多项式进行重新拟合,或加入更多的数据进行重新拟合,直到误差可接受。
(3)求出效能值
根据统计试验或演示实验或实际测量等手段,得出每个指标的具体值,然后利用构造出的效用函数,即可求出与该指标相对应的效能值。
2.2.2 定性指标效用函数构建
定性指标无法直接获得具体数值,因此,采用标度法进行定性指标的度量,首先将定性指标依据问题的性质划分为若干个等级,确定相应标准,再分别赋予0~1.0之间的量值,评估时对应所划分等级和标准给定各定性指标的效能值。各定性指标等级划分及定义见表1。

表1 定性指标等级划分表
定性指标的效能值为:

其中,N为专家人数,xi表示第i个专家对指标X的评估值。
2.2.3 总效能值计算方法
多属性效用函数型态是一种组合法则,一般可分为两种:一是加法模式,包括线性加法模式、高阶加法模式、交互作用加法模式等;二为相乘模式,包括联合模式、解离模式等。典型加法模式两属性效用函数形式如下所示:
K1、K2分别为x1、x2的权重,当x1、x2相互独立时:

在此,认为各个指标相互独立,则效能值可表达为:

上一层次指标的效能值等于与其对应的所有下一层次指标的权重乘以各自的效能值,用相同的方法进行逐层计算,得到最后的总保障效能值。
3 数值仿真实例
本文以某型装甲车辆快速出动能力评估为例,说明用效用函数模型评估装备保障效能的过程。
3.1 保障资源配置效用函数
保障资源配置情况是一个定性指标,则可以采用前面介绍的定性指标效用函数的求法,邀请10位专家对其按照表1的标准进行打分,分数为(0.85,0.8,0.83,0.75,0.7,0.75,0.8,0.75,0.78,0.8),根据式(1)计算,则该参数的效能值为y4=0.781。
3.2 平均故障间隔时间效用函数
平均故障间隔时间门限值为160 km,对应效能值为0.6;目标值为500 km,对应效能值为1.0。通过前面介绍的标准效用测定法,得到曲线上的其他点(240,0.65)(280,0.675)(300,0.7)(335,0.725)(350,0.75)(400,0.8)(450,0.9)(480,0.95),调用MATLAB7.0绘制出效用曲线的大致形状,如图4所示。
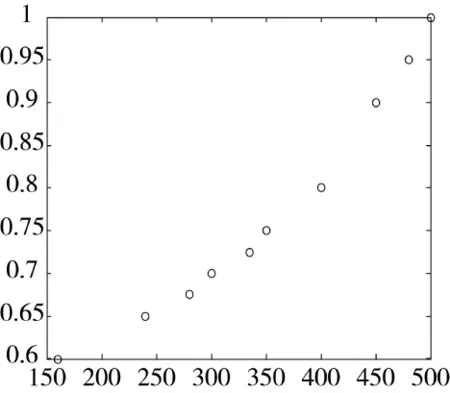
图4 效用函数曲线散点图

图5 拟合后的曲线和原数据点图
然后,调用polyfit(x,y,n)函数进行二次拟合,得到的曲线拟合函数为y1=0.000 002 617x12-0.000 59x1+ 0.633 4,拟合后的曲线和原数据点如图5所示。
单纯从图上来看,拟合的很好,但为准确起见,还是要进行误差分析。在指标值为500时,利用拟合曲线函数计算出的效能值为0.992 55,误差为0.00745,误差很小,可以接受,故平均故障间隔时间指标的效用曲线函数为y1=0.000 002 617x12-0.000 59x1+ 0.633 4。
最后,通过实际验证,得到平均故障间隔时间指标的真实值后,则可代入该曲线函数,得到该指标的效能值为0.718 1。
3.3 平均修复时间的效用函数
目前,平均修复时间门限值为2 h,对应效能值为0.6;目标值为0.5 h,对应效能值为1.0。平均修复时间为4 h时,效能值为0。在2 h~4 h之间时0~0.6线性插值,小于0.5 h时效能值为1.0。则它的效用函数曲线为线性。利用MATLAB拟合后的曲线及原有数据如图6所示。拟合曲线函数为y2=-0.286 5x2+ 1.154 1。通过实际验证,得到平均修复时间指标的真实值后,代入该曲线函数,得到该指标的效能值为0.922 0。
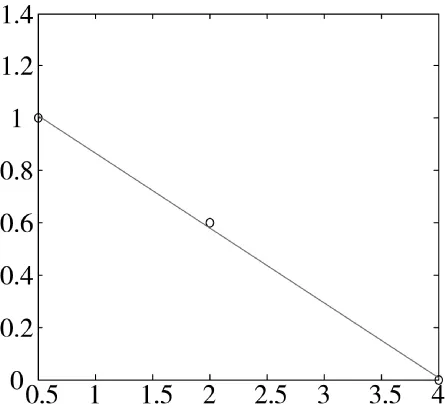
图6 拟合后的曲线和原数据点图(1)
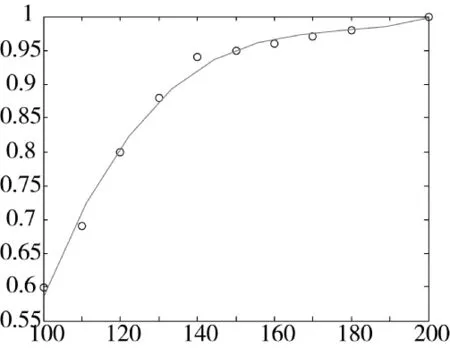
图7 拟合后的曲线和原数据点图(2)
3.4 受油速率的效用函数
目前,受油速率门限值为100 L/min,对应效能值为0.6;目标值为200 L/min,对应效能值为1.0。通过前面介绍的标准效用测定法,得到曲线上的其他点 (110,0.69)(120,0.8)(130,0.88)(140,0.94)(150,0.95)(160,0.96)(170,0.97)(180,0.98)。调用polyfit(x,y,n)函数进行3次拟合,得到的曲线拟合函数为:
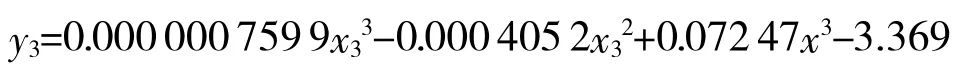
拟合后的曲线和原数据点如图7所示。
在指标值为200时,利用拟合曲线函数计算出的效能值为0.997 9,误差为0.002 1,拟合曲线可以接受,通过实际验证受油速率的真实值后,它对应的效用值为0.936 5。
3.5 快速出动能力的评估
根据式(3)可知:

则

3.6 灵敏度分析
根据得到的各指标的权重值,以及保障资源配置y4、平均故障间隔时间x1、平均修复时间x2、受油速率x34个指标的效用曲线函数,可得出快速出动能力的拟合函数为:
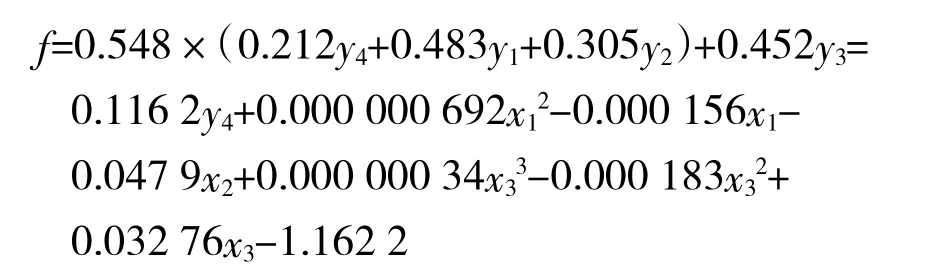
当4个指标各增加1%时,考察快速出动能力的变化情况,进行灵敏度分析,可得表2结果:

表2 灵敏度分析表
对于平均修复时间来说,指标值越小越好,所以当指标值增加1%时,快速出动能力的值是减少的,符合实际情况。通过灵敏度分析,可以看出,当受油速率增加1%时,快速出动能力的变化率最大;其次是平均故障间隔时间和保障资源配置情况,而平均修复时间增长时,快速出动能力变化不是很大。
4 结 论
装备保障效能的评估非常复杂。本文建立了装备保障效能评估指标体系,给出了定量定性指标构建效用函数的方法,并用线性加权法逐层合成总保障效能。通过对装备保障效能的评估,可以找出其中的薄弱环节,为装备优化提供了一定得科学依据。同时本文中的方法,还可以进行多个设计方案、保障方案的权衡分析,从中选出满足作战任务的最佳设计方案和与之相配套的保障方案。
[1]郑金忠,陆四海,李友虎.基于效用函数的航材保障效能评估[J].物流技术,2007,26(8):246-249.
[2]胡 杰,刘晓东.效用函数的装备保障效能分析与评估[J].火力与指挥控制,2012,37(1):100-106.
[3]郭天虎,张笃涛.基于粗糙集的后勤装备保障效能评估指标体系的简化[J].四川兵工学报,2009,30(6):122-124.
[4]岳超源.决策理论与方法[M].北京:科学出版社,2003:112-121.
Evaluation of Equipment Support Efficiency Based on Theory of Utility Function
WANG Qin-qin1,2,SONG Tai-liang3,TANG Wei-da4,ZHAO Xiao-yi5
(1.Academy of Armored Forces Engineering,Beijing 100072,China;2.Unit 72726 of PLA,Jinan 250023,China;
3.China Defense Science Technology Information Center,Beijing 100072,China;
4.Support office of Yantai Guard Section,Yantai 264000,China;5.Academy of Equipment,Beijing 101416,China)
In this paper,the meaning of equipment support efficiency and its evaluation are demonstrated.According to the thinking of capability-performance-characteristics,the paper builds a scientific and rational equipment support efficiency evaluation indexes system,gives the way of building utility function for quantitative and qualitative index,builds the equipment support efficiency evaluation model and demonstrates its validity by means of example.
equipment support,utility function,efficiency evaluation
E92
A
1002-0640(2014)11-0076-04
2013-09-05
2013-11-25
王琴琴(1985- ),女,山东济宁人,博士生。研究方向:保障性评价。

