变分不等式与非扩张映像不动点的迭代逼近问题

洪 泽，郝 彦

（浙江海洋学院数理与信息学院，浙江舟山 316022）

1 引言和预备知识

设H是实Hilbert空间,C是H的非空闭凸子集.S:C→C是非线性映像,T:C→H是非线性映像.用F(S)表示S的不动点集.

若‖Sx-Sy‖≤‖x-y‖,∀x,y∈C,称S是非扩张映像.

若〈Tx-Ty,x-y〉≥0,∀x,y∈C,称T是单调的.

若存在常数 t＞0,满足〈Tx-Ty,x-y〉≥t‖x-y‖2,∀x,y∈C,称 T 是强单调的.

若存在常数t＞0,满足〈Tx-Ty,x-y〉≥t‖Tx-Ty‖2,∀x,y∈C,称T是逆强单调的,也称为t逆强单调的.

变分不等式的求解是最优化方法的一个重要分支.人们对变分不等式的兴趣始于对力学问题的研究.到了上个世纪60年代,变分不等式才作为一门数学学科被人们广泛研究.

经典变分不等式问题是求u∈C,满足〈Tu,v-u〉≥0,∀v∈C(1.1).本文,用VI(C,T)表示问题(1.1)的解集.显然,变分不等式问题等价于不动点问题.u∈C是问题(1.1)的解,当且仅当u是映像PC(I-λ)T的不动点,其中λ>0.

最近,许多专家学者对变分不等式问题(1.1)的解集和Hilbert空间中的非扩张映像不动点解集的公共元进行了广泛研究,详见参考文献[1-3].

令A,B:C→H是两个非线性映像,求（x*,y*）∈C×C,满足

其中λ,η是常数.

2008年,CENG等[2]研究了变分不等式(1.2)的迭代逼近问题,建立了问题(1.2)和一个非扩张映像不动点问题的强收敛定理.

本文受CENG等的启发,研究变分不等式与非扩张映像不动点的迭代逼近问题.

为了证明本文的主要结论,我们需要以下引理.

引理1.1[2]给定x*,y*∈C,其中y*=PC(x*-ηBx*),(x*,y*)是问题（1.2）的解当且仅当x*是映像D:C→C的一个不动点,其中 D(x)=PC[PC(x-ηBx)-λAPC(x-ηBx)].

引理1.2[4]设｛xn｝｛,yn｝是Banach空间X的有界序列,｛βn｝是[0,1]上的序列且假设对于所有正整数

引理1.3[5]假设｛αn｝是非负实数序列,满足 αn+1≤(1-γn)αn+δn,其中｛γn｝是(0,1)中的序列,当｛γn｝｛,δn｝满足如下条件时

引理1.4[5]令C是严格凸Banach空间E的闭凸子集,｛Tn｝是C上的非扩张映像.的,正数序列｛λn｝满足则对于是有定义的,非扩张的且

2 主要结论

定理2.1设C是实Hilbert空间H的一个非空闭凸子集,T,A:C→H分别是t,a的逆强单调映像.令S:C→C是具不动点的非扩张映像.假设Ω∶VI(C,T)∩F(S)∩F(D)≠φ,其中映像D由引理1.1定义.令u∈C,x1∈C,序列｛xn｝由下式生成

其中｛αn｝,｛βn｝,｛γn｝是[0,1]上的序列,μ1,μ2,μ3∈[0,1]满足μ1+μ2+μ3=1,λ∈[0,2a],η∈[0,2b],r∈[0,2t].当上述序列满足以下条件

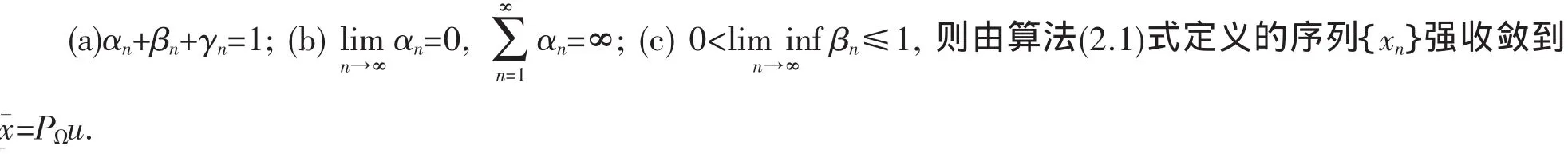
因为A是a逆强单调映像,于是对于任意的x,y∈C,有

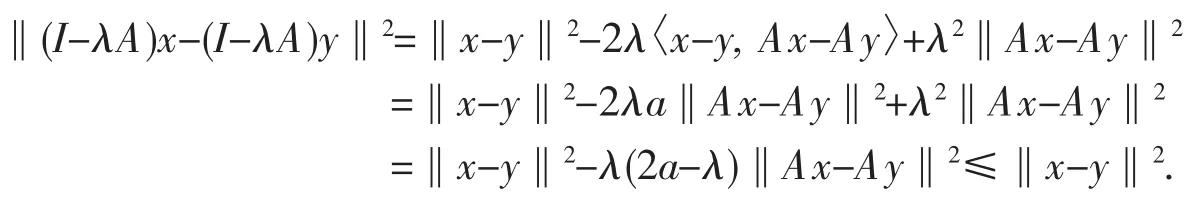
因此I-λA是非扩张映像.同理可证I-ηA,I-rT也是非扩张映像.

因VI(C,T)=F(PC(I-rT)),PC(I-rT)是非扩张映像可得FP(F,T)是闭凸的.

由引理1.1知D=PC[PC(I-ηA)-λAPC(I-ηA)]=PC(I-ηA)PC(I-ηA).则映像D是非扩张映像,即F(D)是闭凸的,于是PΩu有定义.

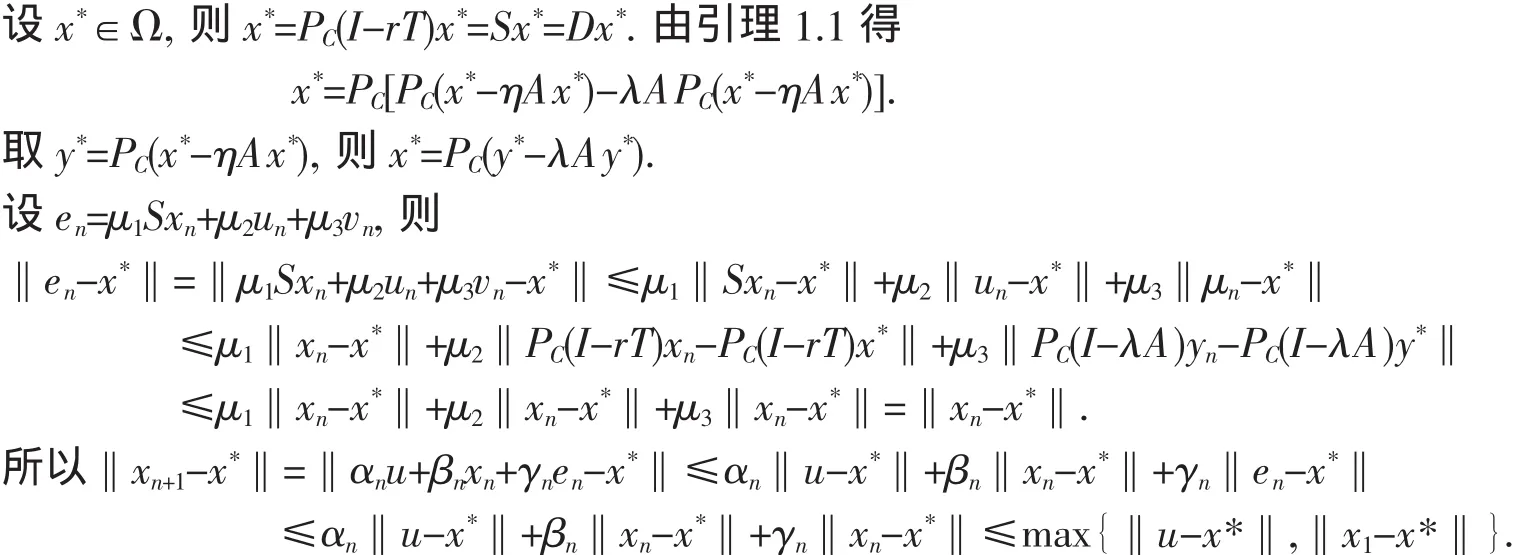
即｛xn｝是有界的.同理可证｛un｝,｛vn｝,｛yn｝有界.

由(2.1)式有

因为｛xni｝有界,则存在｛xni｝的子序列｛xnij｝弱收敛至ξ.不失一般性,不妨设ξ.

定义映像 Q：C→C 满足 Qx=μ1Sx+μ2Trx+μ3PC(I-λA)PC(I-μA)x,∀x∈C.

由引理1.4可知Q是非扩张映像,满足

最后注意到

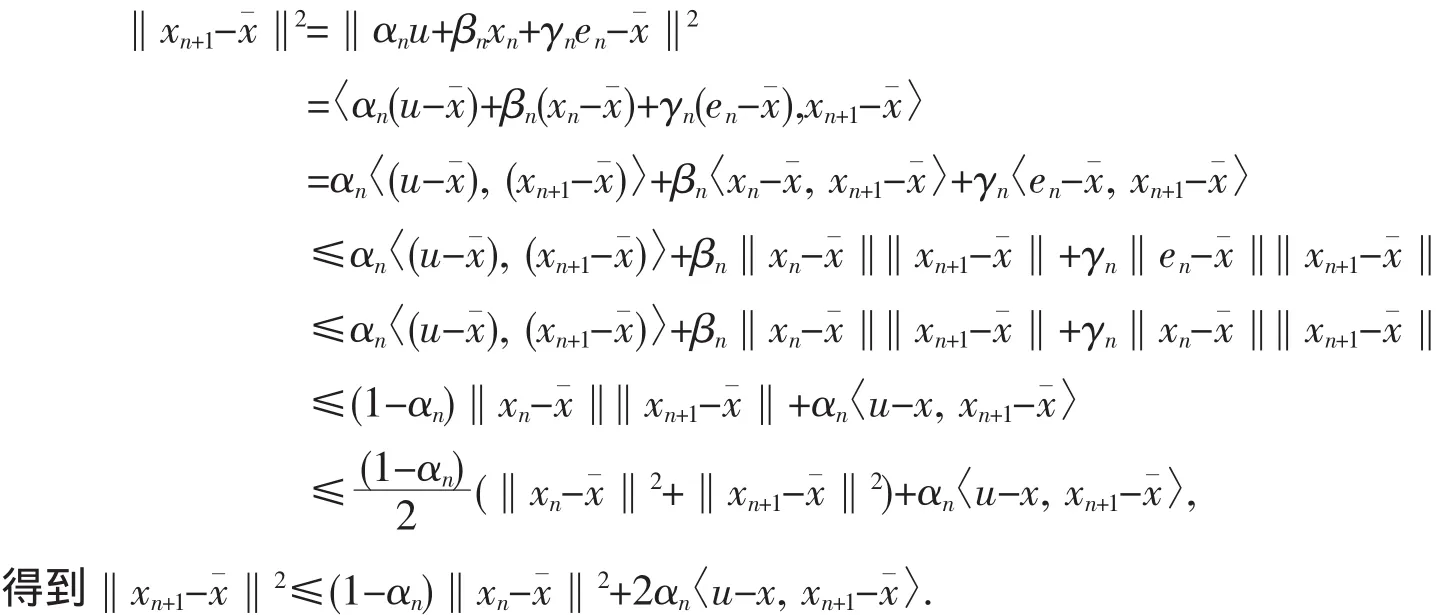
[1]CENG L C,YAO J C.Relaxed viscosity approximation methods for fixed point problem and variational inequality problems[J].Nonlinear Anal,2008,69:3 299-3 309.

[2]CENG L C,WANG C Y,YAO J C.Strong convergence theorems by a relaxed extragradient method for a general system of variational inequalities,Math[J].Methods Oper Res,2008,67:375-390.

[3]IIDUKA H,TAKAHASHi W.Strong convergence theorems for nonexpansive mappings and inverse-strongly monotone mappings[J].Nonlinear Anal,2005,61:341-350.

[4]SUZUKI T.Strong convergence of Krasnoselskii and Mann′s type sequences for one-parameter nonexpansive semigroups without Bochne integrals[J].J Math Anal,2005,305:227-239.

[5]XU H K.Iterative algorithms for nonlinear operators[J].J London Math Soc,2002,66:240-256.