高校师生博弈——基于教学过程的视角

牟勇，董丰，周国苗，黄秀峰

（安徽理工大学经济管理学院，安徽淮南 232001）

高校师生博弈
——基于教学过程的视角

牟勇，董丰，周国苗，黄秀峰

（安徽理工大学经济管理学院，安徽淮南 232001）

建立教学过程中师生的课堂博弈、考试博弈和综合测评博弈模型，求解出模型的纳什均衡，得出结论：（1）在课堂博弈中，当信息完全时，学生努力，老师认真，信息不完全时，老师不认真的概率远大于认真的概率；（2）在考试博弈中均衡为学生作弊，教师监考不严格；（3）在综合测评中均衡结果为学生作业认真，老师不严格。据此提出五点建议来提高教学质量：（1）建立合理的听课打分制度，（2）建立教考分离制度，（3）建立透明的信息体制，（4）实行教学内容的标准化，（5）建立合理的师生奖惩机制。

师生博弈；纳什均衡；教学质量；教学过程

一、引言

近年来，高等教育质量引起全社会的高度关注。教育质量的贡献者主要是教师和学生，而高校师生关系是一个比较复杂的体系，教学过程中高校师生之间的问题广泛存在，主要表现在教学过程中高校师生缺乏交流、关系冷淡以及责任意识淡薄，进而导致高等教育质量堪忧，师生满意度均不高。本文在众多学者的研究基础上，试图从教学过程的视角对师生博弈进行分析，期望能提出提高教学质量的一些建议。

二、高校师生博弈

（一）高校师生博弈的基本假设

（1）假设师生都是理性人，即师生双方都追求自身收益最大化。师生的行为只受收益的影响，不受道德、情感等社会因素的影响。这个假设标准非常高，不一定能满足。但该假设可以让我们得出除道德外的因素是如何影响师生的行动的，这正符合我们的研究目的，因为我们不能把教学质量的提高寄托在道德和情感上。

（2）假设老师认真相对于不认真时要付出一定的成本，但成本较小。该假设用于确定老师在不同情况下的收益。

（3）假设学生的综合测评（包括考试成绩，作业认真情况等）综合为学生作业认真与否，学生不存在智力问题，认真则学生综合测评通过。该假设用于确定学生在不同情况下的收益。

（4）假设整个教学过程中老师知道学生的全部信息，而学生不一定知道老师的信息。该假定非常符合现实，因为老师是知道教学的全过程的，但学生可能不知道全过程。

（5）在整个过程中假设作业认真与努力是一致的，即平时努力的学生的作业也认真。

（二）高校师生博弈

基于教学过程的视角，把师生博弈划分成课堂博弈、考试博弈和综合测评博弈三个相互关联的阶段。课堂博弈是整个教学过程中的核心，在课堂教学中，老师可以通过各方面了解学生的信息，但学生不一定完全了解老师，所以师生博弈可能是完全信息博弈，也可能是不完全信息博弈。

1、课堂博弈

在课堂博弈中，参与人为学生和任课老师，学生有努力与不努力两种行动，老师有认真和不认真两种行动。表1是参与人选择不同策略的收益矩阵。

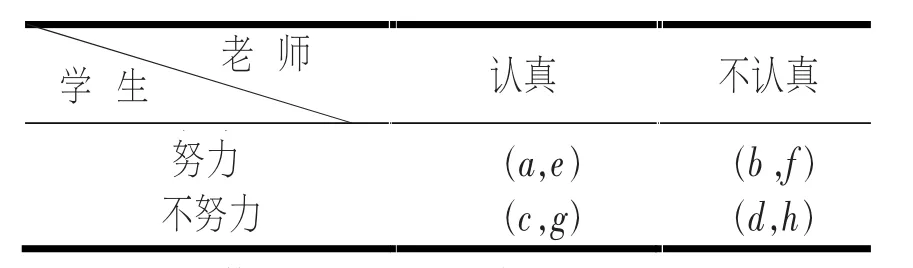
表1 课堂博弈

（1）完全信息下的课堂博弈

信息完全时，努力的学生的收益受老师的影响较小，不努力的学生受老师的影响大；而学生努力与否对老师的收益影响不大。

学生努力时，老师认真学生的收益a大于老师不认真学生的收益b，即a＞b；学生不努力时，老师认真则学生的综合测评很难通过，老师不认真时则易通过，所以收益d＞c。学生努力的收益比同等条件下不努力的收益大，所以b＞d，a＞c。综合得：a＞b＞d＞c。

老师认真时，若学生努力老师的成就感和满足感较大，即e＞g；当老师不认真时，学生努力与否并不对老师的收益构成影响，此时老师既没有对努力学生的满足感也没有对不努力学生感到愤怒，所以，f=h。综合得：e＞f=h＞g。

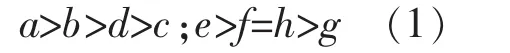
根据下划线法，该博弈的唯一纯战略纳什均衡为（努力，认真）。

（2）不完全信息下的课堂博弈

此处的信息不完全是指学生不了解老师，老师了解学生，与完全信息相比，老师的收益不发生改变。如果学生不了解教学过程和监考、综合评分的公正性，认为老师权力很大，则其感觉到自己的努力也不会有高收益，即相对于努力，不努力的收益更大，d＞b。综合可得：

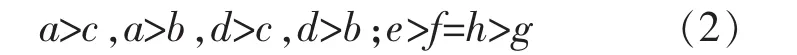
根据下划线法，该博弈存在两个纯策略纳什均衡：（努力，认真）和（不努力，不认真）。由奇数定理（Wilson 1971），一定存在一个混合策略纳什均衡。

设学生努力的概率为α，则学生不努力的概率为（1-α）；老师认真的概率为β，则老师不认真的概率为（1-β）。老师和学生的收益期望表示为（3）。

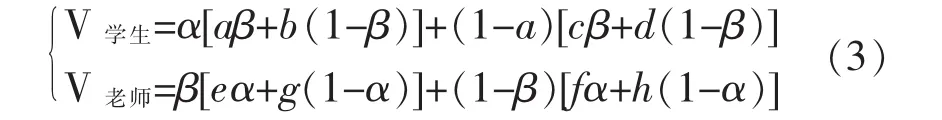
对学生和老师的收益期望求最大值，得一阶条件（4）。

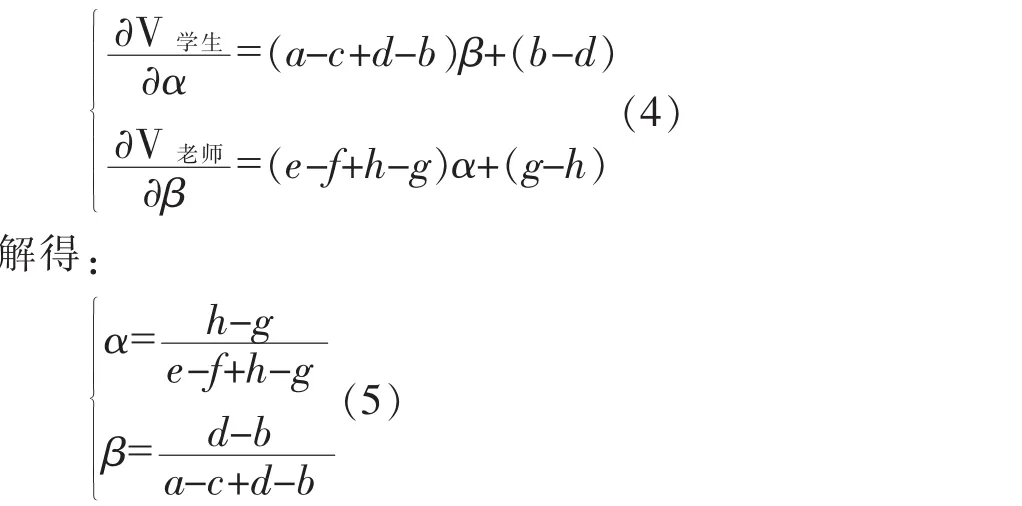
由于d-b＞0、a-c＞0、h-g＞0和e-f＞0，利用函数单调性可知α是（h-g）的增函数和（e-f）的减函数，β是（d-b）的增函数和（a-c）的减函数。

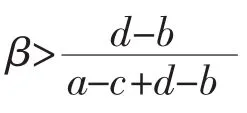
2、考试博弈

在考试博弈中参与人是学生和监考老师（最好不要是任课教师），参与人的行动是：学生有作弊与不作弊两种行动，老师有严格和不严格两种行动。参与人的收益在算例（见表4）中分析。

3、综合测评博弈

在综合测评博弈中参与人为学生和任课老师，参与人的策略为：学生有作业认真与作业不认真两种行动，老师有负责和不负责两种行动。参与人的收益在算例（见表5）中分析。

（三）博弈的算例

取学生或老师的收益范围在0-10之间选择，收益越大，满足程度越高。10表示参与人的收益达到最大，而0表示参与人没有取得收益，6表示“及格”或者不受外界影响。读者可以在下面的例子中取不同的值，做类似的计算。

1、课堂博弈

在完全信息下，由（1）可取学生的各收益分别为a=10、b=7、c=4和d=6；老师的各收益分别为e=9、f=8、g=7和h=8，得表2。

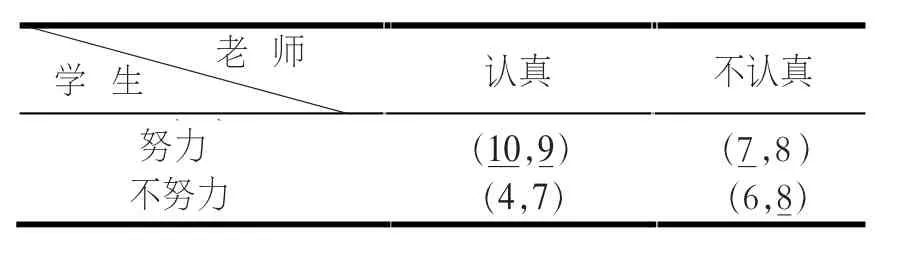
表2 完全信息课堂博弈

由表2可知，该课堂博弈存在唯一的纯战略纳什均衡（努力，认真）。均衡下双方收益为（10，9）。

在不完全信息下，d与b的大小关系发生改变，学生的收益要满足（2），可取d=8，其余不变，得表3。

表3 不完全信息课堂博弈

由表3可知，该博弈存在两个纯战略纳什均衡（努力，认真）和（不努力，不认真），还存在一个混合战略纳什均衡。将表3中的数据带入（5）中得α= 0.5、β=0.14，即在均衡情况下，学生各以0.5的概率选择努力和不努力，老师以0.14的概率选择认真，以0.86的概率选择不认真，这就是混合战略纳什均衡。只要老师认真的概率大于0.14，学生的最优选择就是努力。

2、考试博弈

在考试博弈中，老师严格时的收益要比不严格小。老师严格时，学生作弊则会被抓，导致不及格，收益为0，而老师须为监考严格付出成本，收益取为7；学生不作弊，发挥正常水平，收益取为6，老师严格，学生不作弊，老师监考时相对轻松，其收益为8；老师不严格时，学生不作弊时发挥正常水平，收益为6，学生作弊很难被抓住，而且可以因作弊获得更高分数，收益取为8；如果老师监考不严格，则无论学生作弊与否，由于其不必付出精力，其收益为9。收益矩阵如表4。

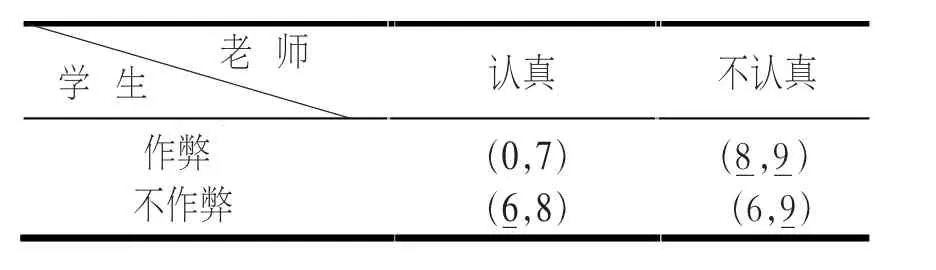
表4 考试博弈

由表4可知该考试博弈中存在唯一的纯战略纳什均衡（作弊，不严格）。该均衡下师生双方的收益为（8，9）。

3、综合测评博弈

在综合测评博弈中，老师负责时，学生作业认真则正常通过，学生的收益取为8，老师负责付出成本，但同时也因学生努力得到满足感和成就感，老师的收益取为8；若学生作业不认真，很可能会导致测评不及格，学生的收益为0，老师并未得到满足感和成就感，收益下降为7；老师不负责时，收益不受学生的行动影响，不必为负责付出成本，老师的收益上升，取为9；若学生作业认真，正常通过测评，收益为7；学生作业不认真仍然会因为老师的松懈而勉强通过测评，收益为6。收益矩阵如表5。

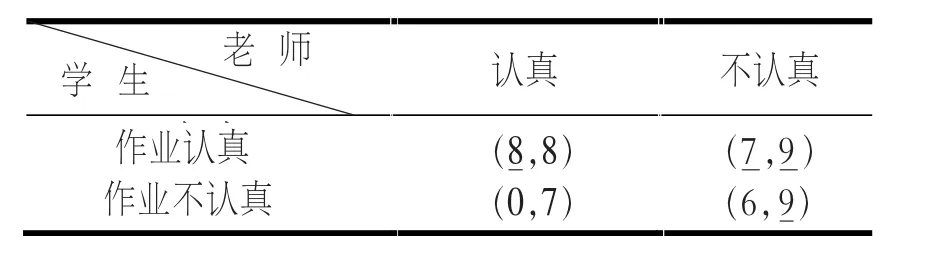
表5 综合测评博弈

由上述收益矩阵可知，该综合考评博弈中存在唯一的纯战略纳什均衡（作业认真，不负责），该均衡下师生双方的收益为（7，9）。

三、结论

由以上博弈算例的均衡结果可得以下结论：

（1）在课堂博弈中，当信息完全时，均衡结果为（努力，认真）；一旦信息不完全，学生不了解教学的全过程，则（努力，认真）和（不努力，不认真）为纯战略均衡。在算例中，混合战略纳什均衡时学生选择努力与否的概率相等，但是老师选择不认真的概率远大于认真的概率。所以，可能状态是，学生不努力，老师不认真。老师认真的概率稍微大一点点（在算例中是0.14），学生就会选择努力，这说明老师的教学态度非常影响学生的行动。

（2）在考试博弈中均衡结果为（作弊，不严格），老师选择不严格的收益优于选择严格时的收益，学生冒着作弊被惩罚的风险选择作弊。常见的现象可能学生作弊，老师不严格考风考纪。

（3）在综合测评中均衡结果为（作业认真，不认真）。常见的现象可能是学生努力作业，老师以不负责的态度批改或点评。

（4）在考试和综合测评博弈中，老师的最优策略都是消极的（不严格或不负责），在课堂博弈中，信息完全时，老师的最优选择是认真，但是在信息不完全的课堂博弈中，博弈的均衡仍然是老师选择消极的策略，教学过程中老师消极行为可能出现。

四、建议

（一）建立合理的听课打分制度

针对结论（1）中师生整体消极的行为，由于目前很多高校仍然不以教学作为评价教师的主要标准，老师不重视课堂授课的重要性，学生深受其害，学习积极性下降。建立科学合理的听课打分制度可以提高老师对教学的重视程度。具体措施可以由教学督导组进行不定期听课，每学期进行学生评教。

（二）建立教考分离制度，加强巡考力度

针对结论（2），首先要加强考场管理、教考分离，避免一些考试中老师发现学生作弊而“手下留情”的现象；其次要加强巡考力度，稳定考试环境，通过巡考制度对老师监考情况进行监督；最后应该确立严明的考规考纪，规范学生考试行为与老师监考行为。

（三）建立透明的信息体制，减少学生与老师之间的信息不对称

学生在不完全的信息下对综合测评结果产生怀疑，学生的行为很可能会偏离理性的选择。因此，确保所有学生清楚地了解综合测评成绩得出的全过程就显得非常重要了。信息透明会减少学生对老师的猜测和怀疑，提高学生努力的积极性，让学生明白，学生的成绩不是取决于老师，而是取决于学生自身。如此可以增加师生之间的信任感，和谐师生关系，提高教学效果。

（四）实行教学内容的标准化政策

由于课时短，老师的性格和专业背景等众多原因，存在授课内容主观化和自由化的问题，使得教学效果差，内容不全，学生也缺乏对授课内容的预习，长期积累的结果便是很多学生对课程内容缺乏系统的掌握。教学内容标准化可以解决这个问题。教学内容标准化主要包括：以备课小组的形式明确每门课程的教学大纲、可选教材及参考资料。通过教学内容的标准化，确定教学范围和教学任务，这样既保证老师完成核心教学任务，又可以结合老师的研究特长对教学内容创新，实行教学内容标准化是一个非常有意义的尝试。

（五）建立合理的师生奖惩体制

根据以上博弈分析可知，老师和学生的最优策略都有可能偏向消极的策略，应加大对师生选择消极态度的惩罚力度，建立师生选择积极态度的激励机制。在考试过程中老师需对学生作弊负主要责任，一旦加大惩罚力度，老师选择倾向于严格，学生不敢冒风险；在综合测评博弈中应对学生成绩的公正评定给予制度上的保证，确定老师在评定成绩过程中的责任。如果学生了解到教学的全部过程以及考试过程、综合测评等的全部信息，学生的理性选择是积极的，而不是消极的。要通过制度使学生成为学习上的主动者，教师成为认真负责的教师！

[1]张维迎.博弈论与信息经济学[M].上海：上海人民出版社，2007

[2]RobertWilson.Computing Equilibria of N-Person Games[J].Society for Industrial and Applied Mathematics，Jul.1971

[3]陆苏华，汪福俊.高校学生考试作弊博弈研究[J].科教视点，2010，（7）

[4]沈智祥，陈晨.经济学视角下大学生逃课的博弈分析[J].社会视野，2008，（5）

[5]林志宏.博弈论视野下的和谐师生关系构建[J].浙江师范大学学报（社会科学版），2011，（1）

[6]周娟娟，王玉萍.学分制模式下大学生综合测评优化分析[J].今日南国，2010，（6）

[7]诸濛.浅析成绩考核方式与教学效果的博弈[J].江西青年职业学院学报，2009，（3）

[8]黄蓓.考试作弊行为的博弈分析及对策[J].湖北经济学院学报（人文社会科学版），2009，（12）

[9]林天伦，陈国香.基于博弈论的师生冲突分析[J].教育科学研究，2010，（4）

[10]姚俊廷.高校师生关系的新特点及其成因[J].太原师范学院学报，2009，（7）

G642

A

1009-9530（2014）01-0145-04

2013-11-26

安徽省大学生创新创业训练计划项目（201210361129）

牟勇（1980-），男，安徽理工大学讲师，研究方向：宏观经济，应用计量经济学。董丰（1990-），男，安徽理工大学信息管理2011级学生。周国苗（1993-），安徽理工大学信息管理2011级学生。黄秀峰（1989-），安徽理工大学信息管理2010级学生。