圆柱体与棱柱体混凝土动弹性模量转换关系

何继炜 李福海

（1.同济大学建筑工程系，上海200092；2.西南交通大学土木工程学院，成都610031）

圆柱体与棱柱体混凝土动弹性模量转换关系

何继炜1，2，*李福海2

（1.同济大学建筑工程系，上海200092；2.西南交通大学土木工程学院，成都610031）

共振法测量混凝土动弹性模量是一种非破损检查方法，对于持续的化学侵蚀及反复的冻融循环等导致的混凝土动弹性模量变化的检测非常有效。使用动弹仪测得不同龄期、不同强度等级的棱柱体混凝土试件和圆柱体混凝土试件的基振频率，通过基振频率计算动弹性模量，提出圆柱体混凝土动弹性模量的计算公式。结果表明：混凝土动弹性模量随强度等级的提高而增大，随含水率的减小而降低。棱柱体混凝土试件与圆柱体混凝土试件之间动弹性模量存在相关关系，并建立了计算公式，可供有关规范、标准修订时参考。

共振法，动弹性模量，圆柱体混凝土，龄期，相关关系

1 引 言

混凝土动弹性模量通常用以检验混凝土在经受冻融或其他侵蚀作用后遭受破坏的程度，并以此来评定其耐久性能。本试验测量混凝土动弹性模量的原理是基于共振法。通过共振法测得材料的基频，就可以推知材料的弹性模量，为区别于常规的静力法得到的弹性模量，故称为动弹性模量［1］。该方法具有测量精度高、试验方便等特点。

目前国内规范中只规定了棱柱体混凝土动弹性模量的计算方法和试验方案［1，2］，文献资料中对圆柱体混凝土动弹性模量的研究以及考虑试件形状、大小对混凝土动弹性模量影响的研究很少。工程中，试件制备或者是钻芯取样进行动弹性模量分析时，很多时候要用到圆柱体试件。由几何学可知，在高度相同的情况下，不同截面形状的混凝土体积一般不相等。体积小的试件形成大孔隙的概率相对较低，结构更密实［3］。所以体积小的试件动弹性模量相对较高，这与其他条件相同的情况下，小试件强度高、大试件强度低的原理是一致的。因此，研究圆柱体混凝土动弹性模量的计算方法以及棱柱体混凝土与圆柱体混凝土之间动弹性模量的转换关系非常有必要。

笔者通过对不同强度等级的棱柱体混凝土试件和圆柱体混凝土试件在不同龄期下的动弹性模量进行测定，分析了动弹性模量随龄期和强度等级的变化规律，并发现100 mm×100 mm× 400 mm的棱柱体混凝土和φ100 mm×400 mm的圆柱体混凝土之间的动弹性模量采用线性模型进行回归分析的精度和稳定性最优，并建立了计算公式。

2 试验原理

纵向尺寸L远大于横向尺寸的细长结构，作微小横振动（弯曲振动），满足动力学方程（横振动方程）为

棒的轴线沿x方向，式中y为棒上距左端x处截面的y方向位移，E为动弹性模量，ρ为材料密度，S为截面积，J为某一截面的转动惯量。

用分离变量法求解方程式（1），令y（x，t）＝X（x）T（t），对于等截面的情况，可以求得结构的自振频率为

式中，β为常数。

在自由端边界条件下，棒的两端（x＝0，L）既不受弯矩也不受剪力。根据边界条件可以得到超越方程

解超越方程式（3）得：βnL＝0，4.73，…其中β1L＝4.73。对应的结构振动频率称为基振频率（基频）。将β1L＝4.73代入式（2）中可以得到

式中，f为基振频率。

如果试样不能满足纵向长度远远大于横向长度，就应该乘以一个修正系数T1，即

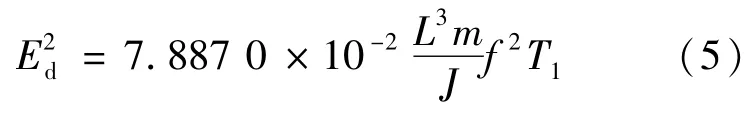
参照《普通混凝土长期性能和耐久性能试验方法标准》（GB／T 50082—2009）中测量混凝土动弹性模量对试件尺寸的要求，当试件为100 mm× 100 mm×400 mm的棱柱体混凝土时，由式（6）可以得到T1＝1.4。将T1＝1.4带入式（5）中，并考虑到J＝a4／12，可以得到棱柱体试件的动弹性模量

《金属材料杨氏模量切变模量及泊松比测量方法（动力学法）》（GB／T 2105—91）中对修正系数T1作了定义。该标准中指出该方法除了适用于金属外，还适用于其他均质体。如果不发生分层离析，混凝土从宏观上讲可以看作均质体，因此该标准适用于混凝土动弹性模量的计算。

对于截面边长为a、长度为L的棱柱体混凝土（泊松比取0.2）试件修正系数

单位为GPa。上述计算公式同《普通混凝土长期性能和耐久性能试验方法标准》（GB／T 50082—2009），《公路工程水泥及水泥混凝土试验规程》（JTGE 30—2005）中对100 mm×100 mm×400 mm的棱柱体混凝土试件动弹性模量的计算规定完全相同。验证了混凝土动弹性模量计算中引入《金属材料杨氏模量切变模量及泊松比测量方法（动力学法）》（GB／T 2105—91）中修正系数T1的正确性。

虽然规范中没有对圆柱体混凝土动弹性模量计算作定义，但是根据上述方法同样可以推导。对于截面直径为d、长度为L的圆柱体混凝土（泊松比取0.2）试件修正系数

由式（8）可以得到几种常用尺寸试件的修正系数，该修正系数可以为相关规范和计算提供参考，见表1。

由表1可知，当试件为φ100mm×400mm的圆柱体混凝土时，T1＝1.3。将T1＝1.3带入式（5）中，并考虑到J＝πd4／64，可以得到圆柱体试件的动弹性模量

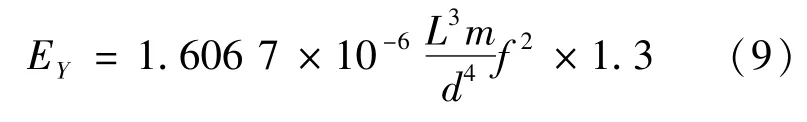
单位为GPa。在高度相同的情况下，不同截面形状的混凝土体积一般不相等，动弹性模量也不相同。体积较小的试件动弹性模量高，体积较大的试件动弹性模量低，这是因为大试件容易形成大孔隙，而小试件形成大孔隙的概率相对较低（假设材料或多或少都存在一定量的孔隙或缺陷）［3］。因此小试件一般要比大试件密实，那么小试件的弹性模量就要高些。这与小试件强度高，大试件强度低的原理相一致。对比式（7）和式（9），对于100 mm×100 mm×400 mm的棱柱体混凝土试件和φ100 mm×400 mm的圆柱体混凝土试件，尺寸已定好，为常数，动弹性模量和质量与基频平方的乘积有关系（质量和基频正好和孔隙、缺陷等有一定的关系），所以要通过试验测得试件的质量和频率，从而计算出动弹性模量，然后用不同的回归曲线对测试结果进行拟合，确定最优拟合曲线，以反映出棱柱体和圆柱体动弹性模量的转换关系。

表1 几种常用圆柱体混凝土试件的修正系数Table 1 Coefficient of correction for common concrete cylinder specimens

3 试验概况

3.1 试件制备

原材料情况如下：水泥为四川金顶（集团）股份有限公司生产的峨眉山牌普通硅酸盐水泥P·O42.5R，密度为2.912 g／cm3；粗骨料来自四川广汉，表观密度为2 719 kg／m3，公称粒径5～20 mm的连续级配碎石；细骨料为广汉河砂，细度模数为2.77，表观密度为2 632 kg／m3，堆积密度为1 630 kg／m3；粉煤灰为遂宁热电厂生产的Ⅰ级粉煤灰，密度为2.059 g／cm3；矿粉为成都混凝土新建材有限责任公司生产的S95级矿粉；减水剂为四川巨星新型材料有限公司生产的JXGBNH1／1型聚羧酸高效减水剂；拌和水为普通自来水，试件制备如图1所示。具体配合比见表2。

表2 混凝土配合比Table 2 M ix proportion of concrete

根据《普通混凝土长期性能和耐久性能试验方法标准》（GB／T 50082—2009）的规定，按上述原材料和配合比制备混凝土试件，按强度等级（C25，C35，C50）划分棱柱体混凝土（100 mm× 100 mm×400 mm）与圆柱体混凝土（φ100 mm× 400 mm）各3组，每组均为3个试件，共计18个。试件分组见表3。

表3 试件分组Table 3 Sam ple grouping

3.2 试验方案

基于共振法，采用型号为DT-10W的动弹性模量仪对每组试件的基频进行测定，通过测得的基频算出动弹性模量。根据《普通混凝土长期性能和耐久性能试验方法标准》（GB／T 50082—2009）的规定，每次测量中，每组测试结果取该组三个试件动弹模的均值。例如某一龄期下C25棱柱体混凝土试件的动弹模等于L25-1到L25-3试件动弹模的平均值：

测试时间从混凝土龄期28 d开始，每隔28 d测量一次，一共测5次。0～56 d混凝土试件在标准养护室进行养护，56 d以后将混凝土试件从养护房取出，置于室外干燥环境中。试件制备与试件测量如图1所示。

图1 混凝土试件制备与测量Fig.1 Preparation and measurement of concrete specimens

4 试验结果与分析

4.1 不同强度等级的混凝土动弹性模量随龄期的变化

将测得的基频通过式（7）和式（9）计算得出各试件的动弹性模量，并求出每组三个试件的动弹性模量在该龄期下的平均值，见表4和表5。

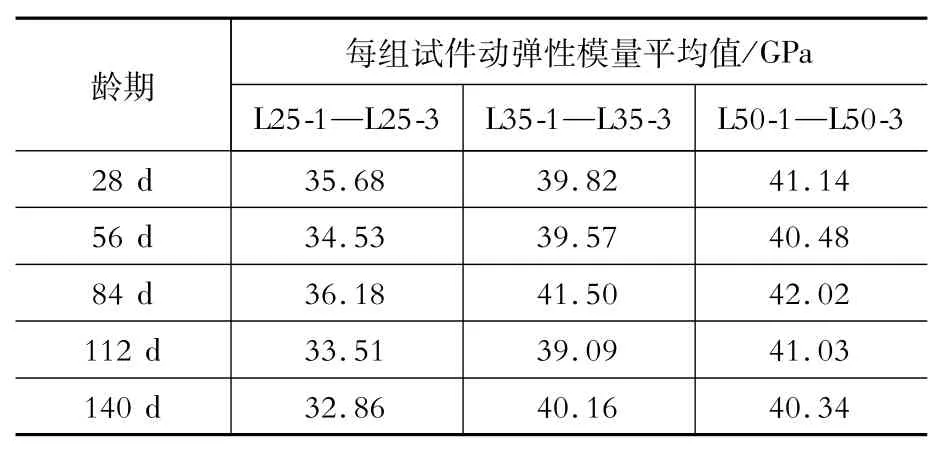
表4 棱柱体动弹性模量数据Table 4 Data of dynam ic elastic modulus for prism

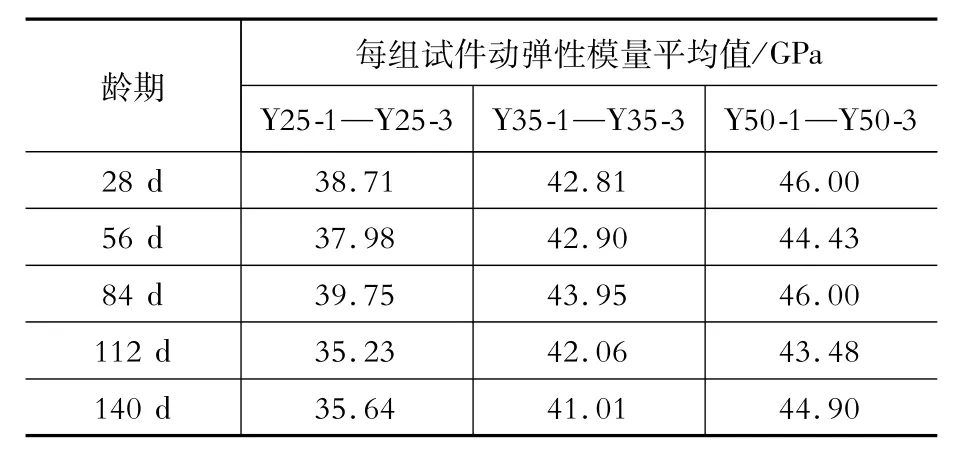
表5 圆柱体动弹性模量数据Table 5 Data of dynam ic elastic m odulus for cylinder

从表4和表5中可以看出，在同一龄期、同一强度等级的条件下，圆柱体混凝土要比棱柱体混凝土的动弹性模量略微大些。这是因为φ100 mm×400 mm的圆柱体混凝土体积小于100 mm ×100 mm×400 mm的棱柱体混凝土（约为79%），所以圆柱体混凝土产生大孔隙和缺陷的概率较小，混凝土结构相对密实，弹性模量较大。

为了便于分析，根据以上数据，分别绘制棱柱体混凝土试件和圆柱体混凝土试件的动弹性模量随龄期的变化规律曲线，见图2和图3。

从图2和图3中可以看出，动弹性模量随着强度等级的提高而增大。这是因为混凝土强度等级越高，水灰比越小，混凝土就越密实，因此弹性模量也就越大。

图2 不同强度等级棱柱体混凝土动弹性模量随时间变化规律Fig.2 Viaration of dynamic elastic modulus for prism concrete under different strength grade and age

图3 不同强度等级圆柱体混凝土动弹性模量随时间变化规律Fig.3 Viaration of dynamic elasticmodulus for cylinder concrete under different strength grade and age

通过对比观察图2和图3中的总共6条曲线，动弹性模量随龄期变化规律具有相似性，相互之间证实了试验结果的可靠性。总体变化规律为：对于某一强度等级的混凝土的动弹性模量，在28～56 d的龄期内变化不大，在56～84 d的龄期内有略微的提高，在84～140 d的龄期内逐渐降低。动弹性模量的这种变化规律和下述两种因素的作用有关：一是在标准养护的条件下，湿度较大，游离水进入水泥混凝土的毛细孔，在试件干燥过程中，由于温度升高，未完全水化的水泥颗粒在游离水存在的条件下继续水化，生成水化硅酸钙和水化铝酸钙，填充了混凝土的毛细孔［3］，增加了混凝土的密实性，此时试件的动弹性模量增加；二是在室内干燥的条件下多余的游离水蒸发会给水泥混凝土带来更多的毛细孔和微裂缝［5］，尤其在水泥水化反应基本结束之后，此原因会占到主导地位，表现为试样动弹性模量的降低。试件在56 d龄期的时候，从标准养护房中取出放入干燥的室内，所以水泥颗粒继续水化，动弹性模量有略微增高。84 d以后水化反应基本完成，游离水蒸发占主导地位，因此动弹性模量逐渐降低。

4.2 棱柱体混凝土与圆柱体混凝土动弹性模量关系

用动弹仪测得不同强度等级（C25，C35，C50）的混凝土试件（100 mm×100 mm×400 mm和Φ100 mm×400 mm）在不同龄期的自振频率，用式（7）与式（9）分别计算棱、圆柱体混凝土的动弹性模量。以每一龄期、每一强度等级下的棱柱体试件动弹性模量为横坐标，圆柱体试件动弹性模量为纵坐标绘出散点图，分别采用线性、抛物线、指数和幂函数四种回归模型，利用最小二乘法进行回归分析，得到4种回归方程和相应的拟合曲线图，如图4所示。

线性函数方程：

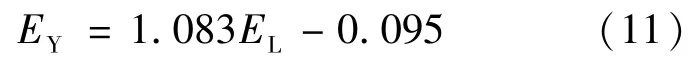
抛物线函数方程：

图4 棱、圆柱体动弹性模量散点图及拟合曲线Fig.4 Scatter diagram of dynamic elastic modulus for prism and cylinder concrete and the fitting line

幂函数方程：

指数函数方程：

式中，EY表示圆柱体混凝土动弹性模量；EL表示棱柱体混凝土动弹性模量。

对以上4类曲线进行拟合精度和稳定性的分析，需要计算出4种回归模型的以下参数。平均相对误差：

相对标准差：

剩余标准差：

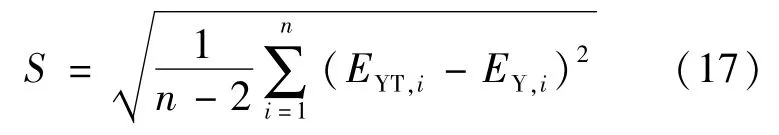
平均值：

回归变异系数：

式（15）—式（19）中EYT，i为第i个圆柱体动弹性模量测试值（取每组三个试件的平均值）；EY，i为第i个圆柱体动弹性模量按回归曲线的计算值；n为圆柱体动弹性模量测试值（取每组三个试件的平均值）的个数。

精度和稳定性计算结果见表6。

表6 精度和稳定性计算结果Table 6 Results of precision and stability

从表6中可以看出，4种回归模型的相关系数相差很小，都约等于0.96。通过对其余指标的比较，可发现采用直线拟合得到的平均相对误差、相对标准差和变异系数均最小，所以直线拟合的效果（精度和稳定性）最优，幂函数次之，抛物线稍差，而指数函数拟合的效果最差。因此，最终确定采用直线拟合的函数模型，即

式中，EY表示圆柱体混凝土动弹性模量；EL表示棱柱体混凝土动弹性模量（对于同一龄期、同一强度等级），适用范围C25—C50。

（1）回归相关系数检验。根据表6得到直线回归分析中，棱柱体与圆柱体动弹性模量的相关系数R＝0.958，当显著性水平α＝0.05时，r0.05＝0.532＜0.958，故相关系数满足要求。

（2）曲线精度检验。由于规范中没有对动弹性模量拟合曲线的精度的要求，所以适当参照测强曲线对平均相对误差和相对标准差的要求［6］：δ＜14%，er＜17%。由表6可知，线性回归模型的平均相对误差和相对标准差均远远小于限值，精度条件满足。

（3）动弹性模量区间预测。圆柱体混凝土动弹性模量概率为95%的近似区间可以取为［EY－2S，EY＋2S］。其中，S为剩余标准差，对于直线拟合模型S＝1.04。故圆柱体动弹性模量的预测区间为［EY－2.08，EY＋2.08］。

5 结 论

（1）建立了圆柱体混凝土动弹性模量的计算公式，得出几种常用尺寸下试件的修正系数，可供相关规范、标准修订时参考。

（2）混凝土强度等级越高，结构越密实，动弹性模量越大。混凝土动弹性模量随龄期变化规律和下述两种因素的作用有关：水化反应的进行程度和游离水的蒸发程度。水化反应的进行增加动弹性模量，游离水的蒸发减少动弹性模量。

（3）通过试验，得出了圆柱体与棱柱体混凝土动弹性模量之间的关系。相同龄期，相同强度等级的棱柱体（100 mm×100 mm×400 mm）和圆柱体（φ100 mm×400 mm）混凝土之间动弹性模量采用线性拟合模型得到的精度和稳定性最高。线性拟合公式为EY＝1.083EL－0.095，相关系数R＝0.958。平均相对误差δ＝1.8%，相对标准差er＝2.35%，变异系数Cv＝2.5%。

［1］ 中华人民共和国交通部.JTGE 30—2005公路工程水泥及水泥混凝土试验规程［S］.北京：人民交通出版社，2005.Ministry of Communications of the People’s Republic of China.JTGE 30—2005 Test methods of cement and concrete for highway engineering［S］.Beijing：China Communication Press，2005.（in Chinese）

［2］ 中华人民共和国建设部.GB／T 50082—2009普通混凝土长期性能和耐久性能试验方法标准［S］.北京：中国建筑工业出版社，2009.Ministry of Construction of the People’s Republic of China.GB／T 50082—2009 Standard for testmethods of long-term performance and durability of ordinary concrete［S］.Beijing：China Architecture and Building Press，2009.（in Chinese）

［3］ 杨彦克，叶跃忠，潘绍伟.建筑材料［M］.成都：西南交通大学出版社，2006.Yang Yanke，Ye Yuezhong，Pan Shaowei.Building Material［M］.Chengdu：Southwest Jiaotong University，2006.（in Chinese）

［4］ 国家技术监督局.GBT 2105—91金属材料杨氏模量切变模量及泊松比测量方法（动力学法）［S］.北京：中国标准出版社，1991.National Bureau of Technical Supervision.GBT 2105—91 Metallic material-standard test method for the Young’s modulus，shear modulus and poison’s ratio（dynamic method）［S］.Beijing：China Standard Press，1991.（in Chinese）

［5］ 乔红霞，周茗如，何忠茂，等.混凝土相对动弹性模量及微观机理研究［J］.粉煤灰综合利用，2009，5：6-10.Qiao Hongxia，Zhou Mingru，He Zhongmao，et al.The study on relative dynamic modulus of elasticity and microstructure of concrete［J］.Fly Ash Comprehensive Utilization，2009，5：6-10.（in Chinese）

［6］ 谢正良，陆洲导.逐层回弹法检测火灾后混凝土强度［J］.结构工程师，2006，22（4）：82-85.Xie Zhengliang，Lu Zhoudao.Layer-by-layer rebound method to access the strength of fire-damaged concrete［J］.Structural Engineers，2006，22（4）：82-85.（in Chinese）

Conversion Relationship of Dynam ic Elastic M odulus between Prism and Cylinder Concrete

HE Jiwei1，2，*LIFuhai2
（1.Department of Building Engineering，Tongji University，Shanghai200092，China；2.School of Civil Engineering，Southwest Jiaotong University，Chengdu 610031，China）

The resonancemethod is a nondestructivemethod tomeasure the dynamic elastic modulus of concrete，which is rather effective to measure the change ofmodulus caused by sustained chemical erosion，repeated freeze-thaw cycles and other factors.Fundamental frequencies of prism and cylinder concrete with different ages and strength grades were tested by using the dynamic modulus instrument.The dynamic modulus could be calculated by the fundamental frequency.Results show that the dynamic modulus increaseswith the improvement of strength grade and it decreases with the decrease ofmoisture content.There is a correlation between the dynamicmodulus of prism and cylinder specimens and a formula was proposed.The formulamay provide some reference for relative codes and criteria.

resonancemethod，dynamic elastic modulus，concrete cylinder，age，correlation

2013－05－14

铁道部科技研究开发计划重大课题（2008G032-5）*联系作者，Email：1130374hjw＠tongji.edu.cn