基于随机模拟的浑河冲洪积扇地区地下水压采风险预报
苏小四,杜守营,杜尚海,宋宪宗,邵广凯,王 璜
1.吉林大学地下水资源与环境教育部重点实验室,长春 130021
2.吉林大学水资源与环境研究所,长春 130021
0 引言
地下水数值模拟技术在地下水有关领域的广泛使用,使其在地下水资源评价、开发利用、管理和规划等方面起到了重要作用[1]。但地下水系统固有的随机性以及研究者主观认识的局限[2],使数值模拟采用的参数带有很大的不确定性,由此可导致模型计算结果的不确定性[3-4]。近年来考虑参数不确定性的地下水流数值模拟的研究,在国内外得到了较好的应用和发展[5],且通过对相关水文地质参数的不确定性分析,可在建立地下水流数值模型的基础上进行随机预报,预报结果可为地下水资源管理提供更可靠依据。
由于长期过量开采地下水,浑河冲洪积扇地区已形成了大面积地下水位降落漏斗,截止到2010年的统计数据表明,仅沈阳城区33m地下水等水位线圈闭的漏斗区面积已达到150km2[6]。为有效地缓解城市地下水超采区地下水位持续下降问题,防止地下水环境的进一步恶化,地下水压采成为解决该类问题的主要方案之一[7],准确预测不同压采方案下地下水水位的恢复情况对超采区地下水资源规划和管理具有重要的实际意义[8-9]。笔者以浑河冲洪积扇地区为研究区,在水文地质参数不确定性分析和地下水流数值模型的基础上,进行压采条件下地下水水位恢复效果的随机预报,并根据预报结果对地下水压采方案进行风险评价。
1 研究区概况
研究区位于浑河冲洪积扇上,地势由东北向西南逐渐降低,平均坡度7.5‰,海拔45~50m,如图1所示。区内地貌以冲洪积平原为主,东北及东南部属风积岗状与波状台地,除东部丘陵区外,均被第四系松散堆积物覆盖。多年平均降水量587.5 mm,多年平均蒸发量826.8mm。浑河是流经该区最大的河流,多年平均流量45.6m3/s,从浑河冲洪积扇的扇顶到扇缘,地表水与地下水转换频繁,在研究区内主要由地表水渗漏补给地下水,局部地段表现为地下水补给地表水。
区内地表为第四系黏性土和亚砂土,其下分别为:以第四系全新统砂砾石和卵石为主的孔隙潜水含水层(Q4)、第四系全新统砂卵石为主的孔隙微承压含水层(Q3)、第四系中、下更新统砂卵石为主的孔隙局部承压含水层(Q2+1)及第三系的风化基岩裂隙水(图2)。其中:孔隙潜水和孔隙微承压含水层在区域内大面积连续分布,且二者水力联系密切,因此将其进一步概化为潜水(微承压)含水层;第四系孔隙潜水(微承压水)和孔隙承压水水头近一致,两者之间是由黏土及亚黏土构成不连续的弱透水层,该弱透水层在区内大部分地段存在缺失;承压含水层底板为相对隔水的基岩;区域地下水流向从东北流向西南,在集中开采的中山、李官堡和竞赛等供水水源地附近存在多处地下水位降落漏斗。
2 研究方法
2.1 水文地质概念模型及数值模型
本次利用地下水模拟系统(groundwater modeling system,GMS)软件建立了研究区地下水流数值模型。在概化研究区水文地质概念模型的基础上建立地下水流数值模型,具体过程如下。
1)含水层系统概化:对区内的钻孔资料进行整理分析,查明上层孔隙潜水(微承压水)与下层孔隙局部承压含水层之间的亚黏土层不连续,且二者之间水头较为一致,存在较为密切的水力联系,因此本次将研究区第四系孔隙潜水(微承压水)含水层与孔隙承压含水层系统概化为一层。

图1 研究区位置及概念模型示意图Fig.1 Study area and conceptual model diagram
2)边界条件概化:水平方向上,模拟区东北及西南部地貌类型属风积岗状台地与风积波状台地,地下水位变化不大,侧向补给量较稳定,研究中确定为二类边界(图1);西部边界因其延伸方向与地下水流向近似平行,且多年变化不大,研究中确定为零流量边界;北部及东南部边界附近虽然地下水动态变化较大,但丰富的地下水水位动态监测数据可以较为精确地刻画边界附近水位的变化规律,研究中确定为一类边界;垂向上,含水层上部主要接受大气降水补给,为水量交换边界,下部因与相对隔水的黏土层、基岩接触,所以定为隔水边界。
3)源汇项概化:含水层的补给主要有降水入渗、河水入渗、地表灌溉回渗、渠系渗漏和地下水侧向径流等;地下水的排泄途径主要以人工开采和潜水蒸发为主,其中开采井通过调整过滤器的位置控制开采层位及开采量,蒸发排泄量通过潜水位与蒸发高程和极限蒸发深度的关系自动计算;河流入渗补给量则通过“River”模块处理成源汇项,根据浑河附近监测孔的地下水水位观测值、河床沉积物渗透系数和厚度等参数对河流属性赋值,由模型自动计算地下水与地表水之间的补排量[10]。
4)数值模型建立:研究区水力坡度平均小于1.0‰,地下水以水平运动为主,流速缓慢,渗流基本符合线性达西定律,且区内含水层的岩性和厚度均有不同程度变化,故模拟区地下水为非均质、各向同性的二维非稳定流,其数学表达式为

式中:K为潜水含水层渗透系数(m/d);H为潜水水位(m);z为含水层底板标高(m);Kz为河床沉积物的垂向渗透系数(m/d);dz为河床沉积物的厚度(m);Hz为河流的水位(m);Qr为补给强度(m/d);Qe蒸发排泄强度(m/d);Qi为开采强度(m/d);μ为潜水含水层给水度;H0为初始水位(m);H1为一类边界点的水位(m);q为二类边界单宽流量(m2/d);x、y为坐标(m);D为计算区范围;Γ1,Γ2分别为一、二类边界。
2.2 参数灵敏度分析
灵敏度是衡量地下水流数值模型对参数变化敏感程度的指标,可以反映一种因子的变化对另一因子的影响程度[11]。限于模型概化及调参阶段对水文地质条件认识的主观局限性,模型识别后的率定参数具有较大的不确定性。通过灵敏度分析可对数值模型各参数对地下水位变化的影响程度排序,定性或定量地评价参数不确定性对模拟结果的影响[12-13],识别出对系统总体输出和动态影响较大的参数,进而确定随机模型的变量参数。
灵敏度分析采用因子变换法,首先确定某一参数作为变量因子,同时保持其他参数不变,逐次运行模型后选定验证时段末刻,分别输出各个参数分区中典型观测井的地下水水位值Hi,作为灵敏度分析的评价指标[3,13]。当作为变量因子的参数由初值αk变为(αk+Δαk),相应地,因变量Hi(αk)变为Hi(αk+Δαk)时,单指标的参数灵敏度系数计算公式为

式中:βi,k为水位H对第k个参数在第i个观测点上的灵敏度系数;Hi为i点的水位;αk为第k个参数的初值。
为便于比较不同参数的灵敏度系数,需对式(2)求得的灵敏度系数进行无量纲处理:
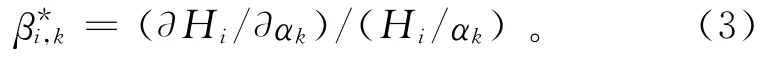
2.3 地下水流预报的随机模型
地下水流预报随机模型的建立调用了GMS软件中的“Stochastic Modeling”模块,参数随机化过程基于蒙特卡罗原理,其前提是假定渗透系数、给水度等随机变量符合一定的概率分布规律,例如渗透系数一般被认为符合对数正态分布,而给水度服从均匀分布[14]。在设置好各个参数概率分布的条件下,首先为每个参数指定均值、标准差、最大值和最小值作为其概率分布的统计特征,然后对参数做多次抽样试验,生成多组输入变量的随机组合,对应每组随机变量分别运行一次 MODFLOW,最后得到若干组水流模型的计算结果,由此获得区内任意点计算水位的统计值[15]。
考虑到随机因素的不确定性对预报结果可能产生波动性的影响,本次研究在参数灵敏度分析的基础上,建立了研究区地下水位预报的随机模型。预报结果不仅能够对压采方案下区域地下水位的动态变化趋势进行预测,还可以根据典型观测井水位的恢复效果对区域地下建筑工程的潜在风险进行评价。
3 结果与讨论
3.1 地下水流数值模拟结果分析
本次研究将浑河冲洪积扇地区剖分成5 025个有效单元格,平均每个单元格面积为0.2km2。模拟期时间步长为1个月。其中:2009年4月25日-2010年4月25日为识别期,以30d为1个应力期,共12个应力期;2010年4月25日-2011年10月25日为验证期,以30d为1个应力期,共18个应力期。
模型识别及验证期典型观测孔的计算水位与实测水位拟合效果如图3所示。可以看出,计算水位与实测水位拟合较好,拟合结果的平均误差为0.05 m,平均绝对误差为0.27m,平均方差为0.31,拟合误差小于0.50m的观测井占其总数的84.50%。由此可见,所建模型基本能正确地反映区内地下水流系统的渗流规律,可在此基础上对模型率定的水文地质参数进行敏感性分析。从计算结果还可以看出,现状开采条件下,在中山、于洪、竞赛、李官堡等水源地出现分散的地下水水位降落漏斗。
3.2 参数灵敏度分析
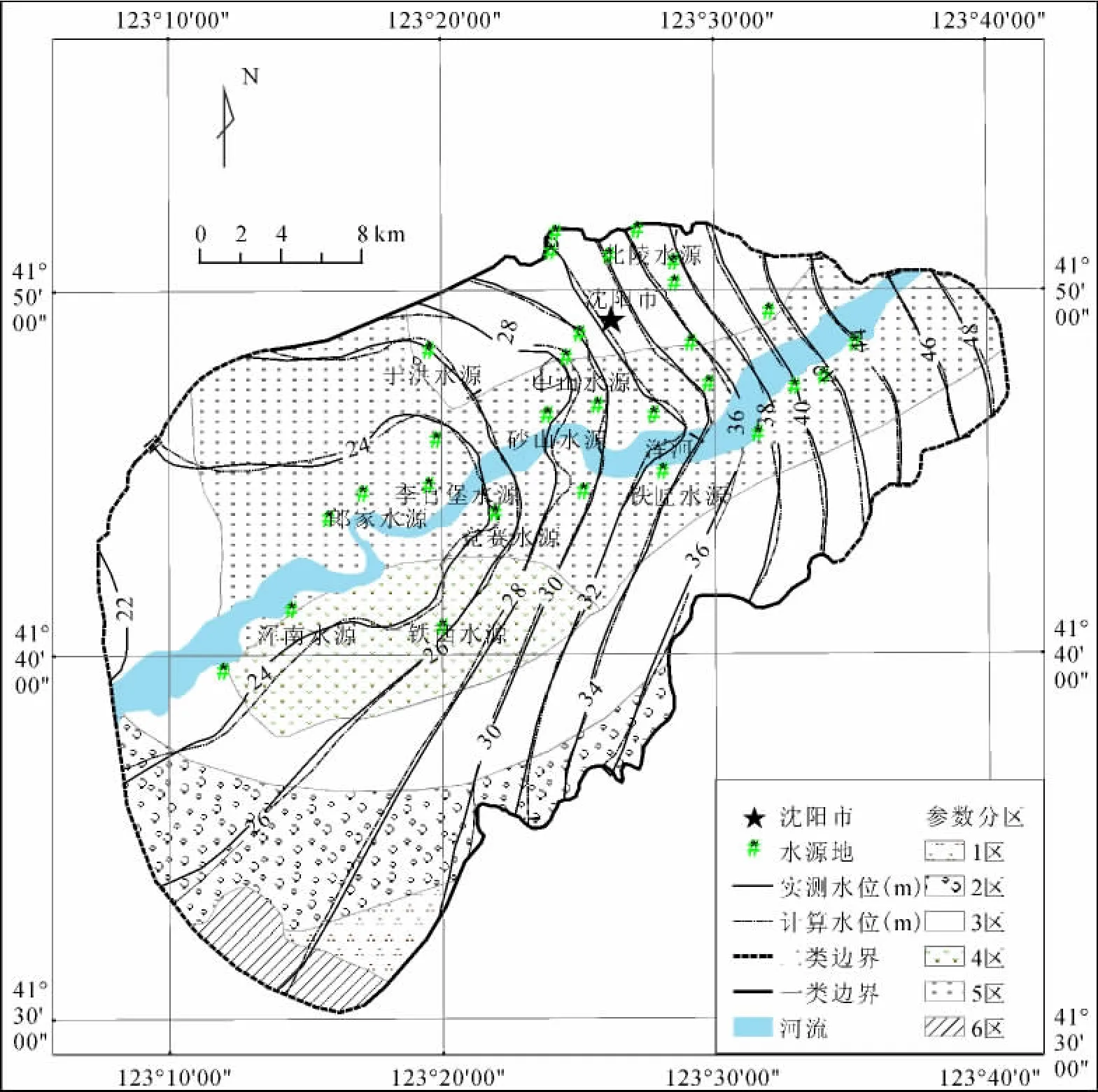
图3 验证期末刻(2011年10月25日)地下水流场拟合及水文地质参数分区图Fig.3 Fitting curve of groundwater flow field and hydrological parameters zoning at the end of the verification period(Oct.25,2011)
结合研究区水文地质条件,本次研究选取渗透系数、给水度、降水入渗补给系数及河床沉积物的渗透系数4个参数进行灵敏度分析。考虑到区内含水层岩性以粗砂和砾石为主,渗透系数应为20~150 m/d,给水度应为0.15~0.35[16];而验证后的渗透系数为33~121m/d,给水度为0.11~0.29,水文地质参数分区情况如图3所示。相对于渗透系数和给水度,河床沉积物的渗透系数和降水入渗补给系数无明显的制约条件;因此在保证渗透系数和给水度取值范围合理的前提下,确定各个参数的变化幅度在率定值的±30%之间。
根据研究区渗透系数分区和灵敏度计算方法,可以得到渗透系数的灵敏度计算结果(图4)。从图4可以看出,第5分区的渗透系数最为敏感,主要是因为该分区为浑河冲洪积扇的河漫滩,含水层岩性变异显著,其他3个参数的计算结果也显示第5分区的参数灵敏度系数比较大。因此本次研究对第5分区各个参数灵敏度分析结果做了对比分析,结果如图5所示。可以看出:地下水水位对含水层渗透系数的变化最敏感;其次是给水度,而对河床沉积物渗透系数和降雨入渗补给系数的灵敏性较差;渗透系数和给水度在其率定值附近对称性增加或减少时,灵敏度系数也呈现出对称性的变化规律,即参数变化幅度增大时,灵敏度系数随之增大。

图4 各分区渗透系数灵敏度对比Fig.4 Permeability coefficient sensitivity of each partition
3.3 地下水流随机预报结果分析
如果不考虑参数随机性,则预报模型中水文地质参数是确定的,因此其模拟结果相当于随机模拟的一个特例,不具有统计特征;而采用参数随机模型进行地下水位预报,能更真实地逼近客观的水文地质条件,统计结果能提高预测结果的精度,从而减少决策误差。本次研究在参数灵敏度分析的基础上,选取渗透系数和给水度作为随机变量,并确定随机变量的变化范围,其中渗透系数的变化范围为率定值的±30%之间,给水度的变化范围为率定值的±20%之间,再为每个随机变量指定初始值、最大值、最小值、均值及标准差,其中初始值取模型验证阶段得到的参数率定值,标准差取区间长度的20%,相关的随机参数设定如表1所示。

图5 第5区参数灵敏度分析结果Fig.5 Parameter sensitivity results of the fifth partition

表1 随机参数的输入设定Table 1 Random parameter settings
地下水流模型中一类边界的地下水位是由大气降水、蒸发等气象因素及人类活动(主要是地下水开采)对影响半径内各动态监测井的水位影响共同决定的,因此进行一类边界条件水位预测时,分别考虑了上述2种影响因素后复合叠加处理[17]。根据Theis公式近似计算出设计开采量在一类边界上各动态观测孔处引起的地下水位降深S[18],预报出各孔在人类活动影响后的末刻水位。大气降水量采用历史降水周期重现法进行预报[11],在对模拟区降水统计资料分析后,设定2006-2022年的降水量为1964-1980年之间降水量的历史重现,由此确定预报期内一类边界在自然和人类活动共同影响下的水位以及研究区内的降水量[7]。蒸发以及河流水位均取多年平均值。预报期地下水的设计开采量是根据研究区未来地下水资源规划方案、在现状开采量的基础上、调整开采量以每年5%的速度递减、以点状开采井的形式输入到模型中的。
地下水流预报模型以验证期末刻(2011年10月25日)的地下水位作为预报期的初始流场,预报时长为10a,在GMS软件中更改模型的运行方式为“Stochastic Simulation”,设置模拟次数为200,则相应地生成200组随机组合数并分别赋值到数值模型中。运行可得200组地下水随机流场,即模型中任意节点在模型末刻均可计算出200个随机水位。
考虑到本次地下水流预报是在限制地下水开采的条件下进行,因此选取以水源地为降落漏斗中心的观测井,将预报末刻(2022年10月25日)作为时间节点,分别输出中山水源地3#观测井和李官堡水源地9#观测井的随机预报水位。通过SPSS 15.0软件对输出结果进行统计,可得到置信区间为95%的条件下地下水位的平均值、最大值、最小值以及标准偏差等信息(图6)。从图6可以看出,受最敏感的渗透系数影响,随机模型的预报水位也基本符合正态分布规律。
选取预报期内每年10月25日作为时间节点,对第5分区部分水源地典型监测井的随机预报结果进行统计分析,可得到预报期内平均地下水位年际动态变化趋势(图7)。从图中可以看出:在地下水开采量以每年5%的速度压采下,相比于预报初始(2011年10月25日),区内地下水水位得到了显著恢复,平均上涨3.3m;地下水水位上升幅度最大的是中山水源地,说明地下水压采可以缓解区域地下水水位下降及降落漏斗扩大等问题。
从压采预报结果可以看出,虽然地下水压采可以有效缓解地下水位持续下降带来的环境问题,但当地下水水位恢复超过地下建筑工程安全设计水位时,地下建筑物的安全将会受到影响,因此需要对地下水压采给周边地下建筑带来的潜在风险进行评价。本次研究中的风险性分析是指地下水开采决策过程中,在系统输入有不确定因素的情况下,研究某一范围内地下水位(H)在一时间段内超过某给定安全水位(Hi)的可能性,即当H≥Hi时的概率P[19-20]。通过对随机预报结果进行统计,可以得到研究区任意一点在预报期内水位超过设计安全水位的概率,从而定量地评价给定的开采方案对地下水建筑安全的风险性。
以水位上升幅度最大的中山水源地为例,到预报末刻中山水源地3#观测井水位恢复情况如表2所示。可以看出:当中山水源地设计的安全水位是29.8m时,在预报期的第10年的渗水风险概率为1.5%,为小概率事件,发生的可能性较小;当该处设计的安全水位是28.8m时,在预报期的第6年(2018年)出现渗水风险的概率为6.5%,而第10年(2022年)发生渗水的风险概率为100.0%。由此可见,按照设计的压采方案对研究区地下水进行开采,未来地下水位的恢复会不同程度地对附近的地下建筑构成渗水威胁,设计安全水位Hi越低,风险出现的时间越早。因此,考虑参数随机性的地下水位风险预报结果能为区域地下水资源风险决策提供依据。
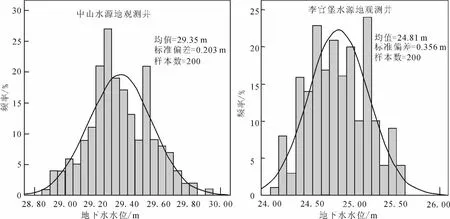

图7 预报期内地下水水位动态变化趋势Fig.7 Dynamic changing trends of groundwater level during the forecast period

表2 中山水源地预报期内不同安全水位对应的风险概率Table 2 Risk probability under different security groundwater levels during the forecast period of Zhongshan water source P/%
4 结论
1)参数灵敏度分析结果表明,地下水水位对含水层渗透系数的变化最敏感,其次是给水度,而对河床沉积物渗透系数和降雨入渗补给系数的灵敏性较差;渗透系数和给水度在其率定值附近增加或减少时,灵敏度系数随之增加或减小。
2)研究表明,压缩开采地下水资源能够有效缓解地下水水位下降带来的环境问题,地下水开采量以每年5%的速度压采时,区内地下水水位平均上涨3.3m,但水位恢复的同时也可能诱发局部地下工程渗水,且地下建筑物的设计安全水位越低,渗水风险越大。
(
):
[1]吴吉春,陆乐.地下水模拟不确定性分析[J].南京大学学报:自然科学,2011,41(3):227-234.
Wu Jichun,Lu Le. Uncertainty Analysis for Groundwater Modeling [J].Journal of Nanjing University:Natural Sciences,2011,41(3):227-234.
[2]束龙仓,朱元生.地下水资源评价中的不确定性因素分析[J].水文地质工程地质,2000(6):6-8.
Shu Longcang, Zhu Yuansheng. Analysis of Uncertainty Factors in Evaluation of Groundwater Resources[J].Hydrogeology & Engineering Geology,2000(6):6-8.
[3]刘佩贵,束龙仓.傍河水源地地下水水流数值模拟的不确定性[J].吉林大学学报:地球科学版,2008,38(4):639-643.
Liu Peigui,Shu Longcang.Uncertainty on Numerical Simulation of Groundwater Flow in the Riverside Well Field[J].Journal of Jilin University:Earth Science Edition,2008,38(4):639-643.
[4]黄修东,杜尚海,崔峻岭,等.平谷地下储水空间调蓄能力及不确定性计算[J].工程勘察,2013(7):35-39.
Huang Xiudong,Du Shanghai,Cui Junling,et al.Computation and Uncertainty Analysis of Groundwater Reservoir Regulation Capacity in Pingu Area[J].Geotechnical Inverstigation &Surveying,2013(7):35-39.
[5]杜守营,鹿帅,杜尚海.基于GMS的地下水流数值模拟及参数敏感性分析[J].中国农村水利水电,2013(8):77-80.
Du Shouying,Lu Shuai,Du Shanghai.Numerical Simulation of Groundwater and Sensitivity Analysis of Parameters Based on GMS[J].China Rural Water and Hydropower,2013(8):77-80.
[6]周浩,王殿武,孙才志,等.沈阳中心城区水源地漏斗恢复调蓄模拟研究[J].水文,2011,31(5):47-51.
Zhou Hao,Wang Dianwu,Sun Caizhi,et al.Numeric Simulation Research on the Recovery of Groundwater Funnel in Core Region of Shenyang City[J].Journal of China Hydrology,2011,31(5):47-51.
[7]杜守营,袁文真,杜尚海,等.压采条件下地下水位恢复对沈阳市地下工程安全影响分析[J].中国农村水利水电,2013(5):20-24.
Du Shouying,Yuan Wenzhen,Du Shanghai,et al.Impacts of Water Table Recovery by Reducing Groundwater Abstraction on Underground Project Safety in Shenyang City[J].China Rural Water and Hydropower,2013(5):20-24.
[8]杜尚海,苏小四,吕航.不同降水丰枯遭遇条件下滹沱河地下水库人工补给效果研究[J].吉林大学学报:地球科学版,2010,40(5):1011-1018.
Du Shanghai,Su Xiaosi,Lü Hang.The Artificial Recharge Effects of Groundwater Reservoir Under Different Precipitation Plentiful-Scanty Encounter in Hutuo River[J].Journal of Jilin University:Earth Science Edition,2010,40(5):1011-1018.
[9]Du Shanghai,Su Xiaosi,Zhang Wenjing.Effective Storage Rates Analysis of Groundwater Reservoir with Surplus Local and Transferred Water used in Shijiazhuang City,China[J].Water and Environment Journal,2013(27):157-169.
[10]曹广祝,强毅,李峰,等.李官堡水源地地下水流场数值模拟及预测[J].中国水能及电气化,2011(8):7-13.
Cao Guangzhu,Qiang Yi,Li Feng,et al.Prediction and Numerical Simulation of Groundwater Flow Field of Liguanpu Wells[J].China Water Power &Electrification,2011(8):7-13.
[11]翟远征,王金生,苏小四,等.地下水数值模拟中的参数敏感性分析[J].人民黄河,2010,32(12):99-101.
Zhai Yuanzheng,Wang Jinsheng,Su Xiaosi,et al.Parameter Sensitivity Analysis in Numerical Simulation of Groundwater[J].Yellow River,2010,32(12):99-101.
[12]李文运,崔亚莉,苏晨,等.天津市地下水流-地面沉降耦合模型[J].吉林大学学报:地球科学版,2012,42(3):806-813.
Li Wenyun,Cui Yali,Su Chen,et al.An Integrated Numerical Groundwater and Land Subsidence Model of Tianjin[J].Journal of Jilin University:Earth Science Edition,2012,42(3):806-813.
[13]束龙仓,王茂枚,刘瑞国,等.地下水数值模拟中的参数灵敏度分析[J].河海大学学报:自然科学版,2007,35(5):491-495.
Shu Longcang,Wang Maomei,Liu Ruiguo,et al.Sensitivity Analysis of Parameters in Numerical Simulation of Groundwater[J].Journal of Hohai University:Natural Sciences,2007,35(5):491-495.
[14]Freeze R A.A Stochastic Conceptual Analysis of Dimensional Groundwater Flow in Nonuiform Homogeneous Media [J]. Water Resources Research,1975,11(5):725-741.
[15]刘猛,束龙仓,刘波.地下水数值模拟中的参数随机模拟[J].水利水电科学进展,2005,25(6):25-27.
Liu Meng,Shu Longcang,Liu Bo.Stochastic Parameter Simulation in Numerical Simulation of Groundwater [J]. Advances in Science and Technology of Water Resources,2005,25(6):25-27.
[16]王大纯,张人权,史毅虹,等.水文地质学基础[M].北京:地质出版社,1995.
Wang Dachun,Zhang Renquan,Shi Yihong,et al.Hydrological Geology Basis[M].Beijing:Geological Publishing House,1995.
[17]卢文喜.地下水运动数值模拟过程中边界条件问题探讨[J].水利学报,2003(3):33-35.
Lu Wenxi.Approach on Boundary Condition in Numerical Simulation of Groundwater Flows[J].Journal of Hydraulic Engineering,2003(3):33-35.
[18]薛禹群,朱学愚,吴吉春,等.地下水动力学[M].北京:地质出版社,1997.
Xue Yuqun, Zhu Xueyu, Wu Jichun,et al.Groundwater Dynamics[M].Beijing: Geological Publishing House,1997.
[19]崔亚莉,王婉丽,杨广元.基于LHS方法的地下水随机模拟及开采量风险性评价[J].地学前缘,2010,17(6):134-139.
Cui Yali, Wang Wanli, Yang Guangyuan.The Parameter Stochastic Simulation and Exploitation Risk Analysis Based on LHS Method[J].Earth Science Frontiers,2010,17(6):134-139.
[20]陆乐,吴吉春.地下水数值模拟不确定性的贝叶斯分析[J].水利学报,2010,41(3):264-271.
Lu Le, Wu Jichun. Bayesian Analysis of Uncertainties in Groundwater Numerical Simulation[J].Journal of Hydraulic Engineering,2010,41(3):264-271.

