通量上边界与水头上边界方法的地下水流系统模拟对比

牛 宏，梁 杏，2，张人权

1.中国地质大学环境学院，武汉 430074

2.中国地质大学生物地质与环境地质国家重点实验室，武汉 430074

0 引言

1940年，Hubbert通过势的数学分析得出了具有上升和下降水流的河间地块示意流网图，打破了传统认为的河间地块地下水水平运动的定势，这是地下水流系统理论出现的雏形［1］。之后，Tóth在加拿大阿尔伯达中部地区观察到有别于Hubbert流网图的地下水流现象，通过分析Hubbert等前人的成果，在均质各向同性介质与严格假定的边界条件下，利用解析解绘制了潜水盆地中具有局部、中间及区域的嵌套式多级地下水流系统，创造性地建立了地下水流系统理论［2－7］，并且认为地形势是控制盆地地下水流系统的关键因素。张人权等［8－9］指出，地下水流系统理论是构建人和自然协调的、良性运转系统的理论基础和有效工具，地下水流系统理论是当代水文地质学的核心概念框架。侯光才［10］、陈蓓蓓［11］应用地下水流系统理论分析了鄂尔多斯白垩系盆地地下水流系统及北京市地下水流系统的演化，对该区各级水流系统特征有了初步的认识。

刘宇、梁杏等［12－13］在进一步开展地下水流系统模式研究时发现，在Tóth地形势控制的模型中，给定盆地上边界水头条件（简称水头法），虽然容易获得解析解，便于理想模型的精确求解，但当单独改变盆地的其他因素（渗透性、盆地深度等）时，盆地补给和排泄也发生变化，水头法不能很好地分析与理解单一因素对地下水流系统模式发育的影响；给定上边界水头固化了盆地的势源与势汇的位置及数目，这与实际盆地潜水面和势汇的变化不相符合，也限制了地下水流系统模式的转化研究。Haitjema和Mitchell-Bruker［14］对地形控制潜水地下水位提出了质疑，Mitchell-Bruker应用定流量上边界的边界元法，得出即使是复杂地形的盆地，改变入渗补给量，也可以出现与Tóth方法不同的水流模式，只有当入渗补给量对介质渗透性的比值较大时，地形才对地下水位起控制作用。为此，梁杏等［15－17］提出了通量上边界研究方法（简称通量法），并开展了相关的物理模拟和数值模拟。

水头法在进行水流系统研究中存在的问题究竟如何，与通量法偏差有多大，应用时限制条件如何，还没有定量的对比模拟分析报道。笔者旨在用数值法进行水头法和通量法的对比模拟，通过模拟结果的定量比较，具体指出水头法模拟的问题与局限性。

1 Tóth典型地下水流系统求解简介

Tóth分别采用一次函数和一次函数叠加正弦波函数，解析出简单与复杂盆地地下水流系统模式［2］。其中，采用一次函数叠加正弦波函数的水头法进行盆地二维流模型的数学方程如下：

式中：h为地下水水头；x、z分别代表以谷底左下方为起点到盆地地下水流动区域中任何一点的水平和垂直距离；Kx、Kz分别为x和z方向的渗透系数；Lx表示x方向总距离；Lz表示盆地底部到盆地最低排泄谷底的深度；h0为上边界定水头值；tanα为盆地谷翼平均坡角正切值（盆地地形斜率）；a为波幅；b＝2π/λ。Tóth利用上述模型，取Lx＝6 096.00 m，Lz＝3 048.00m，a＝15.24m，tanα＝0.02，计算出存在5个高地势和5个低地势的波状上边界；绘制了盆地多级地下水流系统图（图1）；认为在地形复杂的均质各向同性潜水盆地中，地下水流呈现多级次特点，并分别定义为局部的（local system，LS）、中间的 （mittle system，MS）及区域的 （regional system，RS）地下水流系统。

图1 地形复杂的均质各向同性盆地中的多级次水流系统Fig.1 Multilevel flow systems of homogeneous and isotropic basin in complex terrain

方程组（1）和图1显示，在Tóth的求解方法下，渗流区简化为矩形区域，采用水头法求解计算时潜水面、盆地势源与势汇的位置和数目不变；这样求解与实际盆地条件不相符合。实际盆地中，补给区和势汇位置已知时，潜水面（陡缓变化）受到补给量、盆地形态和介质等影响而变化，盆地渗流区仅与潜水面的变化保持一致。为克服解析解的局限性，笔者采用数值法，分别进行盆地水头法和通量法的Tóth典型地下水流模型和变条件模型的改进模拟计算，并对比分析了改进前后的水流系统特征。

2 Tóth典型地下水流系统的数值模拟

2.1 水头法的数值模拟

应用数值模拟软件采用加拿大Waterloo水文地质公司在Modflow的基础上应用现代可视化技术开发研制的Visual-Modflow，它是目前国际一致认可的三维地下水流和溶质运移模拟的标准可视化专业软件系统［18］。

数值模拟方法对Tóth典型模式的渗流区域进行改进，其数学模型类同方程组（1），唯一的区别是模型上部渗流区与上边界水头变化一致，而非Tóth求解时的z＝Lz的水平线。数值模拟取Kx＝Kz＝0.10m/d，有效孔隙度0.25，给水度0.20，总孔隙度0.30，Lx＝6 096.00m，最低谷底高程zmin＝3 048.00m，x方向均分为66列，z方向均分为50层，对上部渗流区进行加密，第一层再加密均分为3层，共52层。模拟得出水流模式如图2所示，采用水头法的数值模拟结果与Tóth解析解的求解结果（图1）基本一致，此时渗流区域最低排泄点为3 048.00m，潜水面最高水头为3 170.00m。在此基础上，笔者进行了通量法的模拟。

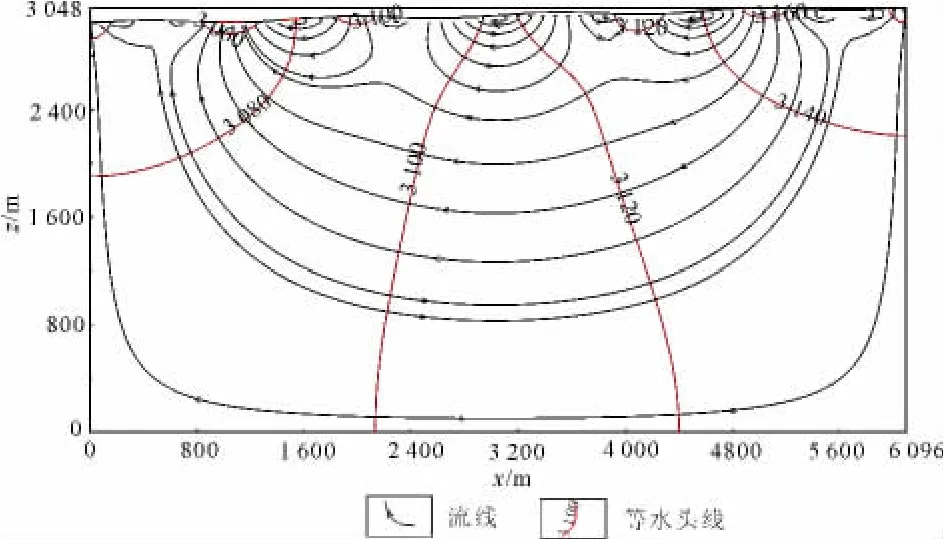
图2 Tóth典型模式（渗流区修正）的水头边界数值模拟结果Fig.2 Given head boundary numerical simulation results of Tóth’s typical model with seepage zone modified

2.2 通量法的数值模拟

通量法的数值模拟是在水头法基础上，将Tóth典型模式（图2）上边界5个补给区（图1中1、3、5、7、9势源区）的补给量转换成平均入渗补给量，在保持盆地补给条件一致的情况下，用通量上边界代替定水头上边界进行模拟。其中：排泄区按照Tóth典型模型的5个排泄点对应设置为5个排泄沟，x方向均分为66列；对5个排泄沟进行加密，每格加密均分成4格，共81列；z方向均分为50层，对上部渗流区进行加密，第一层加密均分为3层，共52层。通量法的模拟结果如图3所示，最低谷底排泄点水头为3 048.00m，潜水面最高水头为3 164.00 m，模拟的实际潜水面较水头法和缓些。对比水头法（图2）与通量法（图3）结果，尽管2种方法的水流模式相同，但通量法的潜水面是计算得出的，并非水头法给定的规则“正弦波”。

图3 通量上边界条件的Tóth典型水流模式数值模拟结果Fig.3 Numerical simulation results of Tóth’s typical model with flux upper boundary

2.3 Tóth典型模式的数值模拟结果对比

用数值法进行Tóth典型模式对比模拟遵循的基本原则是保持盆地水均衡的一致性。Tóth典型模式渗流区修正前后，得出的水流模式相同，修正后盆地水均衡量略大于Tóth解析解（表1）；这是由于此时渗流区与潜水面保持一致，实际渗流区域就会有所增大，在上边界定水头求解时，根据达西定律水均衡量相应增大，图2的补给强度较图1条件增大了4.3%。表1中补给强度为各区补给量除以各区长度所得的单位长度补给量。

表1 Tóth典型模式的渗流区修正前后补给区补给强度对比Table 1 Recharge contrast of Tóth’s typical model with seepage zone modified before and after

Tóth典型模式的水头法与通量法的数值模拟相比，在上边界补给强度相同的条件下，两者模拟的水流模式结果相同，即发育三级嵌套式水流系统（图2与图3对比）。并且通量法保持了5个补给区与水头法的对应关系。利用通量法求解模拟时，潜水面不再固定，而是随上边界入渗条件而形成，模拟结果既符合实际，也能满足改变盆地条件的水流系统模拟的要求。

3 Tóth模型变条件的通量上边界对比模拟

3.1 变条件的水头法模拟

Tóth在典型水流系统的基础上，进行了改变盆地条件（表2）的模拟，如变斜率（A-1与 A-2）、变波幅（A-2与 A-3）以及改变盆地深度（A-3与 A-4）的模拟［2］。Tóth变条件的模拟结果如表2和图4。

表2 Tóth定水头方法变条件的地下水流系统模拟结果Table 2 Groundwater flow-systems simulation results of Tóth’s given head boundary with factor changed

根据变条件求解结果 Tóth［3］指出，地形起伏（对应地下水位波动）是形成嵌套式多级次水流模式的主要因素。当保持地下水位局部波幅不变，各谷底基线的区域性斜率增大时，多个排泄点相对高差增大，指向最低河谷的区域水流系统的范围扩大，局部水流系统缩小退化为滞流带或者消失（图4a、b）；当区域性地形势斜率不变，增大局部波幅时，局部水流系统将增大直至到达盆地底界，区域水流系统消失（图4b、c）；其他条件不变，增加盆地深度（图4c、d），水流下切深度增大，可形成中间和区域水流系统，呈现局部、中间及区域三级水流系统。

Tóth通过上述方法得出了盆地水流模式与“地形势”和盆地深度的关系，从图4和表3可知：1）水头法的变条件模拟中，加大盆地上边界斜率和地形起伏（波幅），实质都是在加大盆地的入渗补给，水流模式都会发生变化；2）定水头条件，水流系统只能从局部系统转化为多级系统；3）加大盆地深度，水流系统也能够从局部系统转化为多级系统，但上边界入渗补给强度同时增加。也就是说，水头法在改变其他任意参数时，存在盆地补给强度同时发生变化的问题。为克服这一模拟问题，下面利用通量法进行对比分析。

图4 Tóth定水头方法在变条件下地下水流数值模拟结果Fig.4 Groundwater flow-systems simulation results of Tóth＇s given head boundary with factor changed

3.2 变条件的通量法模拟

3.2.1 变斜率的模拟条件与结果

变斜率的通量法模拟采用图4a计算的补给结果，在保持上边界补给不变的条件下，设计3组逐渐增大的势汇分布斜率，即调节5个势汇分布高程，进行通量上边界对比模拟，模拟结果如图5和表3。

表3 变斜率的地下水流系统模拟比较Table 3 Simulation comparison of groundwater flow-system with the slope changed

2种方法仅从水流模式上看，都是由一级LS转化成二级RS＋LS再转化成三级RS＋MS＋LS，但水头法在变斜率的同时，上边界补给也发生了改变；而通量法在保持上边界补给不变时，改变斜率即为潜水面发生变化，如果继续加大势汇分布斜率，部分高势汇将失去排泄能力，如图5c只有3个较低势汇起作用。说明存在多个势汇的盆地，除最低排泄区外，在没有进行模拟计算前其他势汇都只能称为潜在势汇，而采用定水头上边界求解时，固定了所有势汇。

3.2.2 变波幅的模拟条件与结果

水头法波幅加大，实质是上边界补给加大，所以变波幅的通量法模拟参考图4b条件采用3组变波幅的水头法补给结果，进行通量法对比模拟，模拟结果如图6和表4。

通量法与水头法变波幅（图6和表4）模拟结果表明：随波幅加大，水流系统模式发生同规律的改变，但通量上边界条件下，潜水面随补给强度和势汇位置自动形成；波幅减小到一定程度（相当于补给强度减小），部分高势汇将失去排泄能力，如图6a只有4个较低势汇起作用，同样也说明存在多个势汇的盆地；除最低排泄区外，在没有进行模拟计算前其他势汇都只能称为潜在势汇；而采用水头法求解时，固定了所有势汇。

图5 通量上边界方法变斜率的地下水流系统模拟结果Fig.5 Groundwater flow-system simulation results of flux upper boundary with the slope changed

图6 通量上边界方法变波幅的地下水流系统模拟结果Fig.6 Groundwater flow-system simulation results of flux upper boundary with the amplitude changed

3.2.3 变深度的模拟条件与结果

变深度的通量法模拟采用图4c计算的补给结果，保持上边界补给不变，设计3组增大盆地深度，进行通量法对比模拟，模拟结果如图7和表5。

从增大盆地深度模拟结果（图7和表5）可以看出：2种方法模拟时，水流模式可能相同也可能不同；水头法模拟，盆地深度增大的同时，盆地补给也增大；而通量法可以在保持上边界补给不变条件下，单一因素地分析盆地深度变化对水流模式的影响。图7结果表明，加大盆地深度，地下水流模式从简单LS水流系统向三级RS＋MS＋LS水流系统方向发育，同时潜水面降低，水面坡度变缓。

表4 变波幅的地下水流系统模拟比较Table 4 Simulation comparison of groundwater flow-system with the amplitude changed

表5 变深度的地下水流系统模拟比较Table 5 Simulation comparison of groundwater flow-system with the depth changed

3.2.4 变渗透系数的模拟条件与结果

为了探讨2种条件下渗透系数对水流系统模式的影响，笔者选取图4b，保持上边界补给不变，进行了一组改变盆地渗透系数的模拟，探讨水头法与通量法水流模式与渗透系数的关系。对比模拟结果如表6和图8。

表6 变渗透系数的地下水流系统模拟比较

Table 6 Smulation comparison of groundwater flow-system with the hydraulic conductivity changed

注：E-2与表2中A-2的模拟条件相同。

图7 通量上边界变深度的地下水流系统模拟结果Fig.7 Groundwater flow-system simulation results of flux upper boundary with the depth changed

图8 通量上边界变渗透系数的地下水流系统模拟结果Fig.8 Groundwater flow-system simulation results of flux upper boundary with the hydraulic conductivity changed

从模拟结果（图8）可以看出：盆地其他条件不变，不论渗透系数增大或减小，通量法的水流系统都会发生改变；而水头法由于固定了上边界水头，根据达西渗流定律可知，模拟计算的补给强度随渗透系数成比例增大（表6），两者比值没有变化，因此盆地水流模式不会发生改变［11］。所以，保持上边界补给不变的通量法，揭示了水流系统变化特征，即随渗透系数增大，潜水面将下降并趋于平缓，盆地部分较高势汇将失去排泄能力（图8c，a），即便是渗透系数极大的情况下，复杂盆地也将仅仅发育单级区域水流系统。

4 结论

1）Tóth利用规则的水头上边界条件，解析得出了典型地下水流模式。然而，水头法模拟固化了盆地势源与势汇的位置和数目，在改变盆地条件的模拟中，盆地潜水面不能随条件的改变而变化，这与实际不相符，也限制了地下水流模式的转化研究；通量法能得出Tóth典型地下水流模式，且潜水面自动形成，在改变盆地条件模拟时，潜水面也随条件而变化。

2）水头法在改变盆地条件（上边界水头分布斜率、局部水头变化波幅、盆地深度和渗透系数）的同时，上边界补给也发生了改变，得出的地下水流模式并不是某种单一因素的影响结果；通量法能保持上边界补给的一致，模拟分析单一因素对地下水流模式变化的影响。

3）基于通量法与水头法在地下水流系统模拟中的优势与不同，在进行盆地地下水流系统理论和实际研究时，应该综合2种方法的特点，结合实际资料条件进行方法的选取与应用。

（

）：

［1］Hubbert M K.The Theory of Ground-Water Motion［J］.The Journal of Geology，1940，48（8）：785-944.

［2］Tóth J.A Theoretical Analysis of Groundwater Flow in Small Drainage Basins［J］.Journal of Geophysical Research，1963，68（16）：4795-4812.

［3］Tóth J.Mapping and Interpretation of Field Phenomena for Groundwater Reconnaissance in a Prairie Environment，Alberta，Canada［J］. Hydrological Sciences Journal，1966，11（2）：20-68.

［4］Tóth J.Groundwater Discharge：A Common Generator of Diverse Geologic and Morphologic Phenomena［J］.Hydrological Sciences Journal，1971，16（1）：7-24.

［5］Tóth J.Gravity-Induced Cross-Formation Water Flow：Possible Mechanism for Transport and Accumulation of Petroleum［J］.American Association of Petroleum Geologists Bulletin，1978，62（3）：567-568.

［6］Tóth J.Patterns of Dynamic Pressure Increment of Formation-Fluid Flow in Large Drainage Basins，Exemplified by the Red Earth Region，Alberta，Canada［J］.Bulletin of Canadian Petroleum Geology，1979，27（1）：63-86.

［7］Tóth J.Cross-Formational Gravity-Flow of Groundwater：A Mechanism of the Transport and Accumulation of Petroleum：The Generalized Hydraulic Theory of Petroleum Migration ［J］.Problems of Petroleum Migration，1980，29：121-167.

［8］张人权，梁杏，靳孟贵，等.当代水文地质学发展趋势与对策［J］.水文地质工程地质，2005，32（1）：51-56.

Zhang Renquan，Liang Xing，Jin Menggui，et al.The Trends in Contemporary Hydrogeology ［J］.Hydrological and Engineering Geology，2005，32（1）：51-56.

［9］张人权，梁杏，靳孟贵，等.水文地质学基础［M］.6版.北京：地质出版社，2011.

Zhang Renquan，Liang Xing，Jin Menggui，et al.Fundamentals of Hydrogeology［M］.6nd ed.Beijing：Geological Publishing House，2011.

［10］侯光才，林学钰，苏小四，等.鄂尔多斯白垩系盆地地下水系统研究［J］.吉林大学学报：地球科学版，2006，36（3）：391-398.

Hou Guangcai， Lin Xueyu， Su Xiaosi，et al.Groundwater System in Ordos Cretaceous Artisan Basin（CAB）［J］.Journal of Jilin University：Earth Science Edition，2006，36（3）：391-398.

［11］陈蓓蓓，宫辉力，李小娟.北京地下水系统演化与地面沉降过程［J］.吉林大学学报：地球科学版，2012，42（1）：373-379.

Chen Beibei，Gong Huili，Li Xiaojuan.Groundwater System Evolution and Land Subsidence Process in Beijing［J］.Journal of Jilin University：Earth Science Edition，2012，42（1）：373-379.

［12］刘宇，贾静.基于 MATLAB小型潜水盆地地下水流动系统模拟研究［J］.地下水，2009（3）：1-3.

Liu Yu，Jia Jing.Study of Groundwater Flow Systems Simulation of Small Drainage Basin Based on Matlab［J］.Groundwater，2009（3）：1-3.

［13］梁杏，牛宏，张人权，等.盆地地下水流模式及其转化与控制因素［J］.地球科学：中国地质大学学报，2012，37（2）：269-275.

Liang Xing，Niu Hong，Zhang Renquan，et al.Basinal Groundwater Flow Patterns and Their Transformation and Dominant Factors［J］.Earth Sciences：Journal of China University of Geosciences，2012，37（2）：269-275.

［14］Haitjema H M，MitchellB S.Are Water Tables a Subdued Replica of the Topography？［J］.Ground Water，2005，43（6）：781-786.

［15］刘彦，梁杏，权董杰，等.改变入渗强度的地下水流模式实验［J］.地学前缘，2010，17（6）：111-116.

Liu Yan， Liang Xing， Quan Dongjie，et al.Experiments of Groundwater Flow Patterns Under Changes of Infiltration Intensity［J］.Earth Science Frontiers，2010，17（6）：111-116.

［16］权董杰.二维盆地地下水流模式与转化规律分析［D］.武汉：中国地质大学，2011.

Quan Dongjie. Analysis of Two-Dimension Groundwater Flow Patterns and Transformation Rules［D］.Wuhan：China university of geosciences，2011.

［17］Liang Xing，Quan Dongjie，Jin Menggui，et al.Numerical Simulation of Groundwater Flow Patterns Using Flux as Upper Boundary［J］.Hydrological Processes，2012.

［18］杨春玲，邢世录，韩爱中.地下水系统数值模拟的研究进展［J］.内蒙古科技与经济，2007（21）：305-307.

Yang Chunling，Xing Shilu，Han Aizhong.The Research Progress of Groundwater System Numerical Simulation［J］.Inner Mongolia Technology and Economy.2007（21）：305-207.