运用频率计算河川基流量方法研究
李计生,王 静
(甘肃省水文水资源勘测局,甘肃 兰州 730000)
基流是地下水和其他延迟的水资源补给河川径流的部分水量[1]。丘陵山区主要是基岩地下水分布区,由于基岩裂隙潜水的分水岭与地表水分水岭相一致,在评价其天然资源时,最宜按流域来进行,基岩风化带裂隙水最终排入地表水系,因此最宜采用河流流量过程线的切(分)割来推算排入河中的地下径流量(基流量)。目前,评价山丘区地下水资源的方法,可归纳为水文分割法、理化分析法和水文-水文地质法等。这些方法都有一个共同的特点,就是在每次评价计算时,都要重新计算分析,且根据个人经验和方法的不同,得出的结论不尽相同,如何建立河川基流量计算的简便实用方法,为准确地评价区域水资源,进行水资源的科学规划与合理配置,寻求一种经济适用又切合实际的河川基流量分割方法,是水利工程建设与国民经济发展的迫切需要。
1 河川基流切割的水文方法
利用实测水文河川径流,根据径流形成原理,把山丘区的河川径流人为地划分为地表径流和地下径流,这种方法称为水文分割法。倪雅茜 等对目前水文界运用的基流分割方法进行了深入的研究,并指出了其优缺点[2],通常用的方法有下列几种。
1.1 直线切割法
1.1.1 枯季最小流量法
用年内枯季最小流量乘以一年的时间(秒数)得出全年地下径流量。基流量因其值因没有包括全部基流而偏小,可作为河川基流量的下限,比较稳定。
1.1.2 枯季最小日平均流量法
选择年内最小日平均流量乘以一年的时间(秒数)得全年基流量。其值也因不能包括全部基流而偏小。1.1.3 枯季最小月平均流量法
以年内最小月平均流量乘上全年的秒数即得全年的基流量,其值比上述两法要大一些。
以上几种方法大同小异,相当于用不同的枯季最小流量作为基准的直线平割法,类似的方法还有枯季最小三个月(八个月)平均流量法、270 d保证流量法等。
1.2 直线斜割法
其做法为:在逐日河川径流过程线上分割河川径流量时,枯季无明显地表径流的河川径流量全部作为河川基流量(俗称清水流量);自洪峰起涨点至河川径流退水段转折点(又称拐点)以直线相连,该直线以下部分即为河川基流量。直线斜割法对于年河川径流过程属于单洪峰型或双洪峰型时特别适用。
1.3 加里宁试算法
加里宁(加里宁-阿巴里扬)试算法,是根据河川基流量一般由基岩裂隙地下水所补给的特点,并假定地下水含水层向河道排泄的水量(即河川基流量)与地表径流量(包括坡面漫流量和壤中流量)之间存在比例关系,利用试算法确定合理的比例系数,再通过对水均衡方程的反复演算得出年河川基流量。此法具有一定的理论基础,物理概念明确,但工作量大,费时费力。
1.4 滤波法
文献[3]所述:“因为没有实在的根据来区分河道中任何时刻的直接径流和地下径流,又因为这两个组成部分的定义是比较任意的,所以分割方法往往同样是任意的。”而滤波法为近年来国际上研究最为广泛的基流分割方法。其原理是从基流(低频信号)过滤地表径流(高频信号),与信号分析及处理中过滤高频信号是相似的,1979年Lyne等于提出该算法[4],Nathan等将其首先用于水文领域[5],Smakhtin等用该法对南非诸流域的日基流进行了分割[6]。滤波法的方程为:
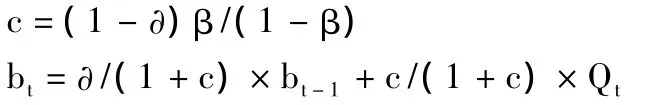
式中:Qt为第 t日的日平均流量(t=1,2,…,365);bt为基流;∂、β 为滤波参数(0p ∂p 1,0 pβp1)。
滤波算法是对径流数据进行多次滤波,符合地下水形成的机理,故本文的基流数据为滤波算法所切割。
2 存在的问题
无论是直线切割还是斜线切割,均忽略了汛期地下水受补给的径流变化过程,其结果是偏小的、不正确的,精度较低。要选用其中的某种方法,要经过分析比较,在对精度影响不大时可应用,成果仅作参考。且在逐日河川径流过程线上,洪峰起涨点比较明显和容易确定,而退水段的转折点往往不容易分辨,分割结果比较粗略。加里宁试算法由于试算量大,计算时段采用日、侯、旬的结果是不同的,一般时段愈长,结果愈大。理化分析法和水文-水文地质法由于成本大,推广起来有一定的难度。如何根据实测水文资料,建立河川基流量计算的简便实用方法,为准确地评价区域水资源,进行水资源的科学规划与合理配置,寻求一种经济适用又切合实际的河川基流量分割方法,是水利工程建设与国民经济发展的迫切需要。
3 年径流频率与基流
3.1 年径流频率与基流的计算
在山丘区可从径流过程中分析出地表径流、壤中流和地下径流3个部分的水资源量,地下径流量(基流量)是指河川径流量中由地下水渗透补给河水的部分,即河道对地下水的排泄量[7]。常年有水的河流切割地区,河水的补给来源有大气降水和地下水排泄。在枯水期,河水几乎全部由地下水的排泄来补给;洪水期间,河水则由大部分洪水和少部分地下水排泄量构成。因此,在河流流量过程线上将泄入河流的地下水量分割出来。作者采用滤波算法的计算机程序,分别计算了1981-2000年长江流域白龙江水系的舟曲和武都,黄河流域洮河水系的李家村、碌曲、岷县和红旗,内陆河流域黑河水系的札马什克、祁连和莺落峡等水文站的径流量频率及基流量,见表1。
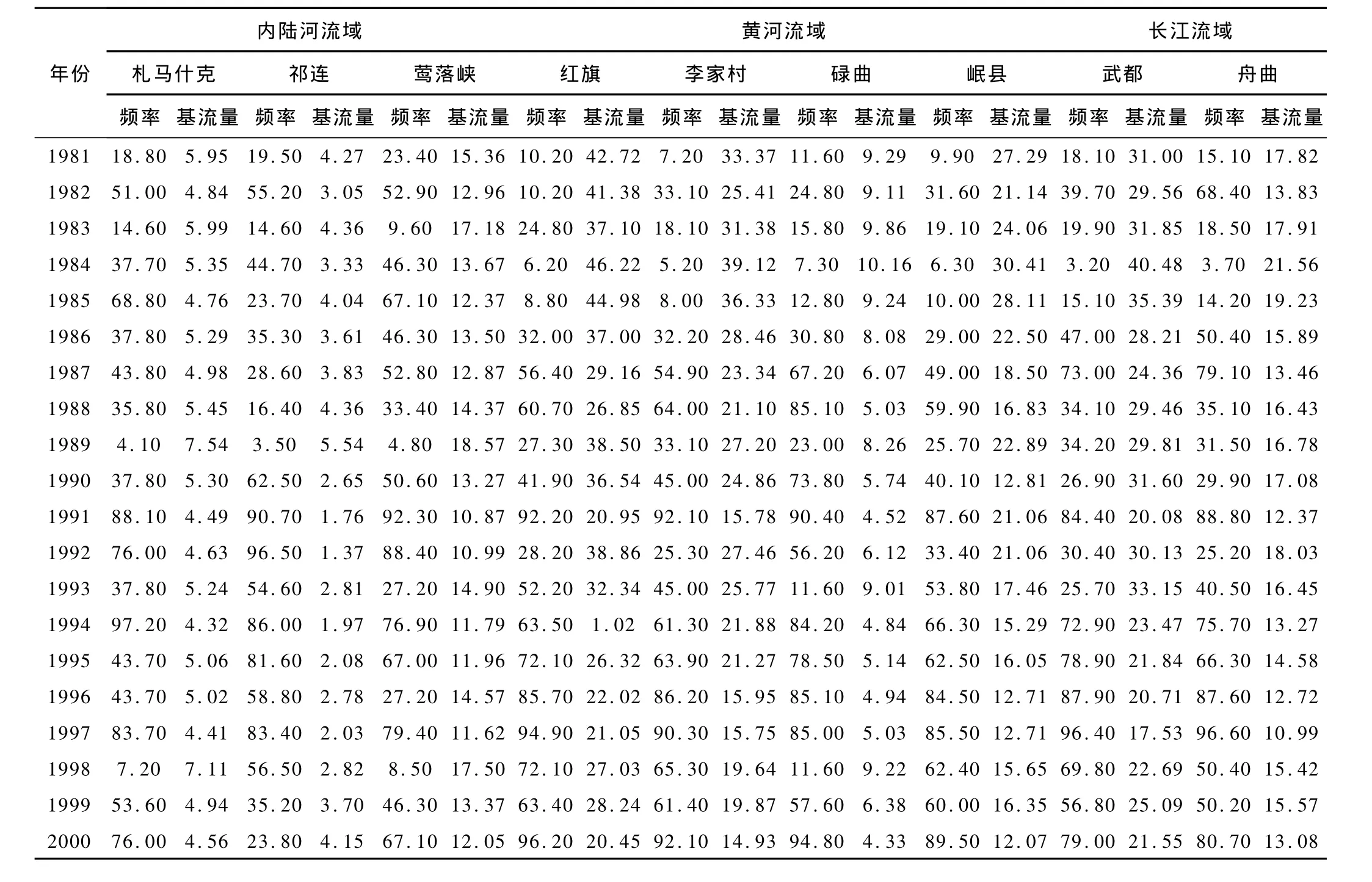
表1 径流频率与基流量104m3
3.2 年径流频率与基流相关模型的建立
运用线性回归,利用表1所列数据,其结果列于表2,可以看出,各计算模型均有较高的判断系数,说明回归结果的拟合程度良好,符合该水文站的水文特性,p值均小于显著性水平0.000 1,置信度高达99.99%,说明自变量频率对因变量基流量有显著影响。建立各水文站的年径流频率与基流计算模型,年径流频率与基流计算模型如下:
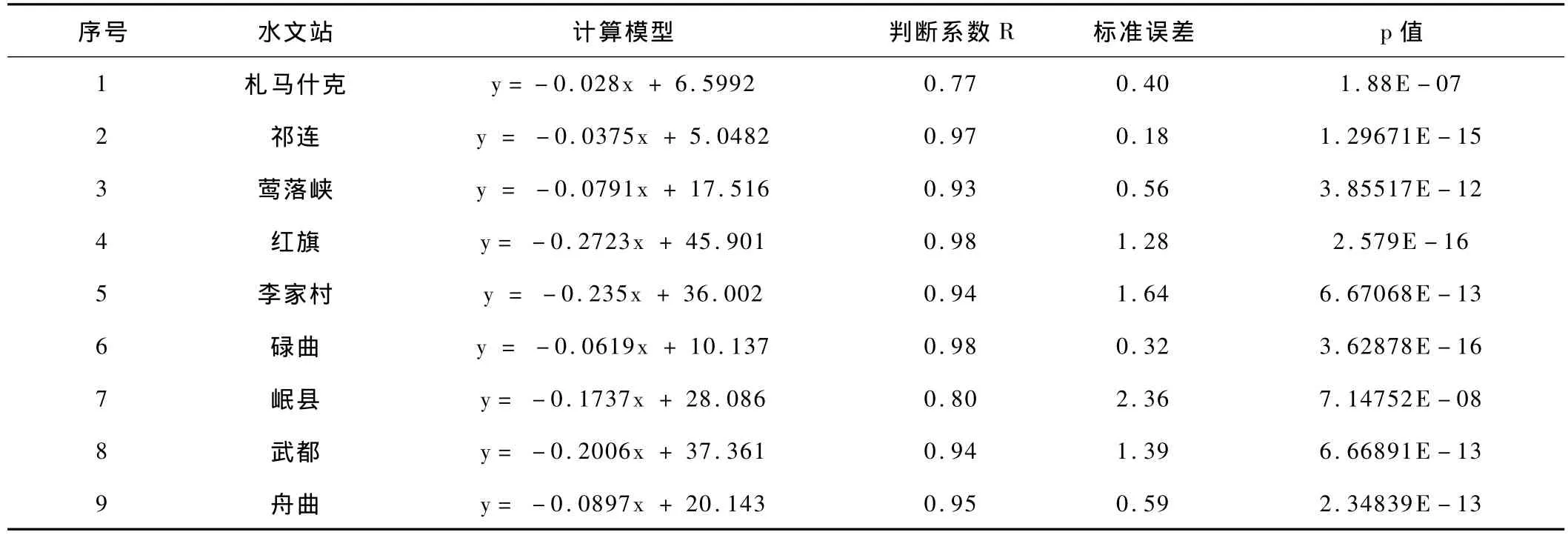
表2 频率与基流相关回归计算统计表

表3 各水文站相关系数表
其中,y*为各水文站的基流量,x为运用PIII型曲线得到的年径流频率值。

图1 内陆河流域基流与频率相关图
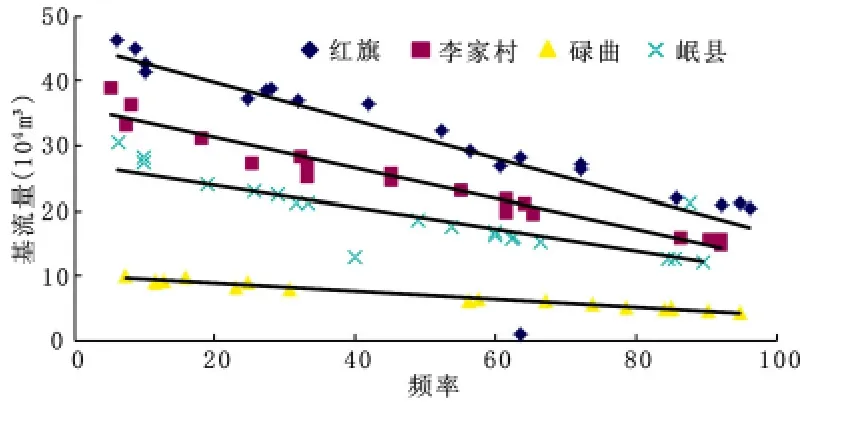
图2 黄河流域基流与频率相关图
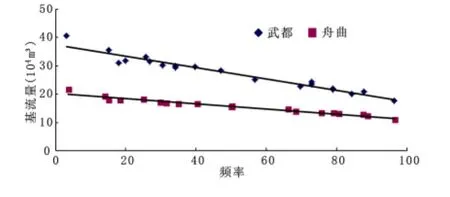
图3 长江流域基流与频率相关图
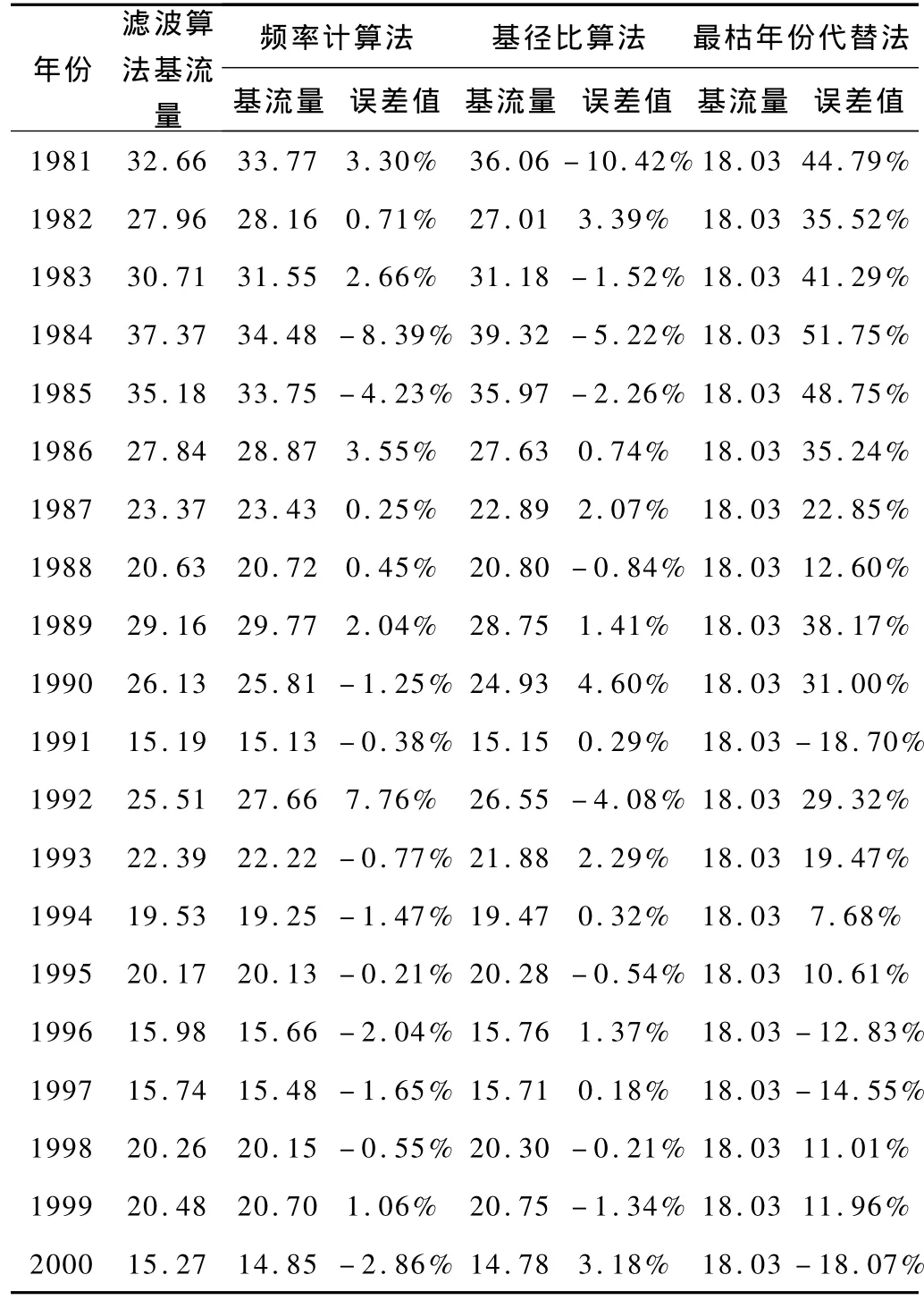
表3 岷县站各种算法统计比较表 104m3/s
3.3 模型的稳定性准确性分析
因为建立的模型为一元回归方程,运用数理统计中的相关系数来分析各站的年径流频率与基流相关模型的稳定性准确性,相关系数(r)反映了两个变量之间联系的密切程度。其取值为0≤|r|≤1。它愈接近1,关系愈密切(r=1就是完全相关的函数关系),所得方程的精度就愈高,其误差平方和就愈小。反之,愈近于零(r=0无关系)。相关程度平价标准:|r|≤1,|r|=1,表示x与y变量为完全的线性相关,也即为确定的函数关系;|r|=0,表示两变量不存在线性相关;0<|r|<1,表示两变量存在不同程度的线性相关。0<|r|≤0.3为微弱相关;0.3 < |r|≤0.5 为低度相关;0.5 < |r|≤0.8为显著相关;0.8 < |r|<1 为高度相关[8]。
查相关系数显著性检验表。当统计样表数N=20时,α=0.05 时,r=0.423,α =0.01 时,r=0.537,本次计算的各水文站的相关系数r值如表2:
可以看成,相关系数均大于置信度为α=0.01时的r=0.537值,通过了显著性检验,并且r值均大于0.8,说明年径流频率与基流高度相关,建立的模型是稳定且准确的。
4 验算
运用岷县水文站年径流频率与基流相关模型的对1981-2000a的资料进行基流计算,并用其他水文方法的计算结果进行比较。结果如表3。从表中可以看出,其误差范围均小于9%,将模型建立后,在以后的工作中,只要得到年径流量,就可以查算出频率,在根据建立的模型,可以快速的计算出当年的基流量,此法具有速度快、精度高的特点。
5 结语
(1)在流域上游,由于流域下垫面条件好,基径比高,河川基流与径流的相关性好,反之,在流域下游,由于各支流的加入,河川径流具有不确定性,故基径比不稳定。
(2)从线性方程的系数为负值来看,说明频率越小,当年径流中洪水组成部分较多,基径比较小,与山丘区的地下水形成原理相一致的。
(3)本次分析计算选择了甘肃不同流域中的其中一个水系的水文站资料进行,主要是寻找一个可行的计算山丘区地下水的经济可行的方法,所建模型只是1981-2000a的20年系列,如要得到准确模型,必须利用长系列的实测水文资料建立准确模型方可运用。
[1]倪雅茜,张文华,郭生练.流量过程线分割方法的分析探讨[J].水文.2005,25(3).
[2]刘光文.工程水文学[M].北京:水利出版社.1981.
[3]莱恩V,豪力里克M.随机变量降雨径流模拟.水文和水资源研讨会,水文与水资源工程协会全国委员会,珀斯,西澳大利亚,澳大利亚,1979.89 -93.
[4]弥敦道RJ,麦克马洪 TA.基流自动化技术评价和衰退分析.水资源研究.1990,26(7):1465 ~ 1473.
[5]斯马赫京 VY,沃特金斯 DA.南非低流量评价.WRC报告.1997.97(1):494.
[6]水庭,施鑫源.地下水水文学[M].南京:河海大学出版社.1993.
[7]李洁明,祁新娥.统计学原理(第四版)[M].上海:复旦大学出版社.2007.

