多处理部件并行优化方法研究

李 钊,郑 红

(北京航空航天大学自动化科学与电气工程学院,北京100191)

多处理部件并行优化方法研究

李 钊,郑 红

(北京航空航天大学自动化科学与电气工程学院,北京100191)

针对多处理单元(PE)并行优化中运行时间和资源消耗随PE数量变化而增加的问题,分析多PE并行中运行时间和资源消耗随PE数量的变化规律,建立基于运行时间和资源消耗的优化目标函数,并从理论上证明优化目标函数最小值的存在性和唯一性,提出基于运行时间与资源消耗的多PE并行优化方法。该优化方法可在最小资源消耗的情况下实现运行时间的最优化。利用灰度共生矩阵和单精度浮点矩阵乘法的多PE优化方法进行验证。实验结果表明,多PE并行的优化方法实现了运行时间和资源消耗的优化,在运行时间上该方法比已有方法最高快6.79倍,在运行时间和资源消耗的综合对比上该方法最高为已有方法的3.3倍,能够实现基于运行时间和资源消耗的优化。

多处理单元并行;优化方法;运行时间;资源消耗;灰度共生矩阵;单精度浮点矩阵乘法

1 概述

多处理单元(Processing Element,PE)是一个能实现特定功能的处理单元,在不同的硬件平台上PE具有不同的表现形式,例如在通用并行硬件平台上一个PE可以是一台PC机或者工作站,在嵌入式并行硬件平台上一个PE可以是一片微处理器芯片,也可以是芯片中的一个核或者是可编程逻辑器件中由逻辑单元组成的能实现特定功能的一个功能模块。根据待处理算法的不同设计不同的PE,以实现特定的功能,PE与PE之间可以并行执行,以提高算法实时性。目前,设计多个PE并行的计算结构实现算法的并行计算,在信号处理和图像处理等领域得到广泛应用。

文献[1]在实现一维快速傅里叶变换(one-Dimensional Fast Fourier Transform,1-D FFT)计算的基础上,以1-D FFT计算单元为核心设计实现2-D FFT的PE,并利用多个PE并行实现二维快速傅里叶变换(two-Dimensional Fast Fourier Transform,2-D FFT)的计算,PE的数量由可使用的硬件资源决定。文献[2]利用图像处理算法的数据并行性,设计基于2D脉动阵列的多PE并行的计算结构,该结构可以完成图像卷积和模板匹配等算法的计算。文献[1-2]利用多个PE的并行执行有效减少了算法的运行时间,但是随着PE数量的增加会消耗更多的硬件资源,而硬件资源是有限的,因此,在改善运行时间的同时,也需要降低系统的资源消耗。文献[3]设计数量可扩展的多个PE线性阵列,实现任意维数的矩阵乘法,PE的数量由存储器带宽和硬件资源决定,PE内采用流水线结构设计,利用数据访问的局部性和可重用性降低资源消耗。文献[4]提出2种计算浮点矩阵乘法的多个PE并行的结构,算法1可实现最大程度的并行,但需要消耗较多的硬件资源和I/O带宽,算法2对算法1进行了改进,通过减少PE的数量虽然增加了算法运行时间,但是也降低了资源消耗,提高了资源的利用率。文献[3-4]在改善算法运行时间的同时开始用各种方法降低资源消耗,但是没有对运行时间、资源消耗与PE数量之间的关系进行分析,未实现运行时间和资源消耗的优化设计。

随着PE数量的增加,算法需要占用越来越多的硬件资源,并且随着PE数量的增加,PE间的通信开销会逐渐增加,布线延时也会随之增加。布线延时的增加会导致运行时间的增加。由于不是设计越多的PE就会得到更好的运行性能,因此本文对PE的数量(P)与PE占用的硬件资源和运行时间等参数之间的关系进行分析,建立运行时间和资源消耗的优化目标函数,实现运行时间和资源消耗的优化。

2 多PE并行运行时间和资源消耗的优化

本文以现场可编程逻辑门阵列(Field Programmable Gate Array,FPGA)为例对多PE的运行时间和资源消耗影响因素及规律进行分析,在FPGA内PE由加法器、乘法器、累加器和比较器等基本功能逻辑单元构成。

2.1 多PE并行资源消耗影响因素

FPGA资源消耗主要包括占用基本可编程逻辑单元的数量和片上存储空间的数量。本文对PE占用基本可编程逻辑单元的数量进行分析。以Xilinx公司Virtex系列的FPGA为例,一个基本可编程逻辑单元(Configurable Logic Block,CLB)由2个slice组成,一个算法的资源消耗最终可由slice的数量来表示。

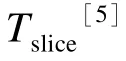
α与Sslice的关系如图1(a)所示,当PE中各个基本功能逻辑单元占用的slice数量即Sslice＜600时,α呈现震荡趋势,当Sslice≥600时,α基本保持不变。因为当PE规模较小时,一个slice中仅利用了部分查找表和触发器,而随着PE设计规模的增加,一个slice中更多的查找表和触发器得到利用,因此,当PE规模较小时,PE占用slice的数量与PE的规模并不呈线性关系,只有当PE达到一定程度后,占用slice的数量与PE的规模才呈线性关系。图1(b)为Tslice与Sslice在比例因子α作用下的关系图,当Sslice＜600时,Tslice与Sslice呈非线性关系,当Sslice≥600时,Tslice与Sslice呈线性关系。

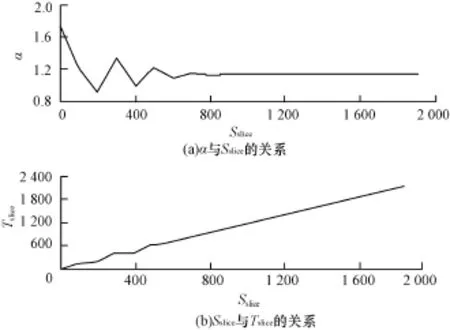
图1 α,Tslice与Sslice的关系

2.2 多PE并行运行时间影响因素

FPGA设计中,可通过布线资源连接不同基本功能单元实现某一特定功能,因此运行时间LE主要由各基本功能单元的运行时间组成的逻辑器件延时Llogic和布线延时Lrouting组成,如式(2)所示。各基本功能逻辑单元的延时Llogic由其实现的功能及采用的FPGA决定。布线延时Lrouting直接由布线的长度决定,因此要计算布线延时需要先正确的估算布线的长度,布线长度可由式(3)计算得到[6]。其中,C表示CLB的数量(可通过slice数量计算得到);p表示Rent系数其值设为0.72。图2为布线长度与CLB数量的关系曲线,随着CLB数量增加,布线长度也随之增加,即PE占用的资源越多就需要更多的布线资源实现逻辑单元之间的连接。

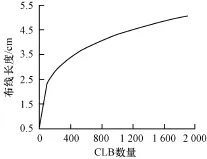
图2 布线长度和CLB数量的关系

至此,布线延时Lrouting可由式(5)计算得到,其中,Lengthbetween_PIPs表示 2个可编程连接点(Programmable Interconnect Points,PIPs)之间的长度;Lbetween_PIPs+Linside_PIPs表示PIPs之间的延时与PIPs内部延时之和。

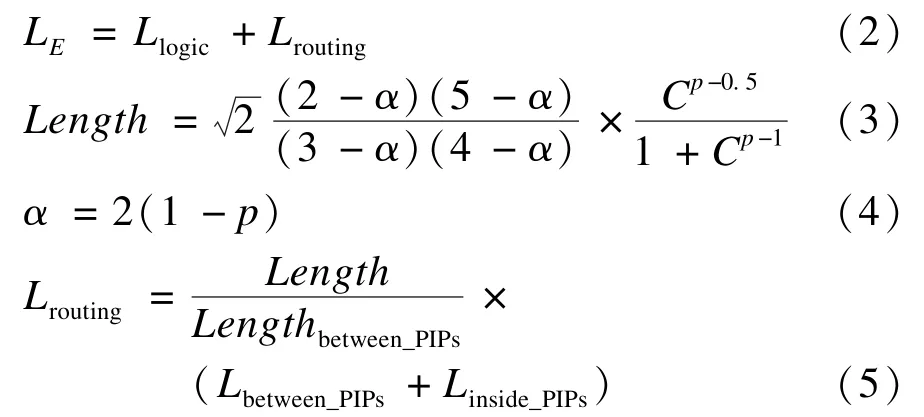
FPGA内部具有短线、长线和全局互联线等布线资源,在布局布线过程中,一个PE占用的资源会集中在一个区域,PE中会消耗较多的短线资源以实现基本逻辑单元之间的互连。为便于计算,设Lengthbetween_PIPs为短线长度,与Lbetween_PIPs和Linside_PIPs都可从相应FPGA文档中得到。

设处理的算法可分为H个并行处理的部分,采用P个PE并行对图像算法进行处理,则待处理算法的运行时间L如式(6)所示。将式(2)、式(3)、式(5)代人到式(6)中即得到P个PE并行处理所需要的延时计算式式(7)。

2.3 优化目标函数

由式(1)和式(7)可得,随着PE数量的增加整个系统的运行时间会越来越小,但是由于受到布线延时的影响,当PE数量增加到一定程度后,系统的运行时间减小的趋势会减弱,而资源消耗会随着PE个数P的增加呈线性增长。要想得到较好运行时间需要较大的资源消耗,运行时间和资源消耗之间是相互矛盾的,需对两者进行优化设计。

因为运行时间和资源消耗具有不同的量纲,两者之间没有一个统一的度量标准,难以直接对其进行优化,所以需要对运行时间和资源消耗进行无量纲化处理,无量纲化公式如式(8)所示,其中,fmin(x)、fmax(x)分别表示f(x)在自变量变化范围内的最小值和最大值。

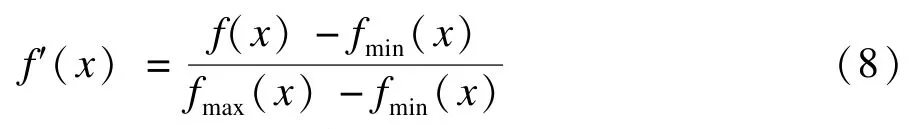
一般P的最小值Pmin为1,此时为串行操作,P的最大值Pmax由图像大小、FPGA硬件资源和具体的图像处理算法决定。由式(1)和式(7)可得,P=Pmin时运行时间L取得最大值Lmax(P),资源消耗Tslice取得最小值Tslicemin(P);P=Pmax时L取得最小值Lmin(P),Tslice取得最大值Tslicemax(P)。利用式(8)可计算得到无量纲化后的运行时间L′(P)和资源消耗T′slice(P)。因为运行时间和资源消耗的优化目标都是实现目标函数的最小化,所以可直接将L′(P)与T′slice(P)相加构造新的优化目标函数U(P),即:

U(P)=L′(P)+T′slice(P) (9)

因为L′(P)和T′slice(P)的值越小系统的整体性能就越优,所以U(P)的最小值点即为系统整体性能的最优点。

现对U(P)最小值的存在性和唯一性进行证明。

证明:

(1)U(P)最小值存在性证明

1)因为L′(P)和T′slice(P)在闭区间[Pmin,Pmax]上为连续函数,所以U(P)=L′(P)+T′slice(P)在闭区间[Pmin,Pmax]上连续,则由有界性定理得{U(P)|P∈[Pmin,Pmax]}有界。

2)设M为U(P)在[Pmin,Pmax]上的下确界,即inf{U(P)|P∈[Pmin,Pmax]}=M。用反证法证明U(P)最小值存在性。

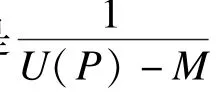
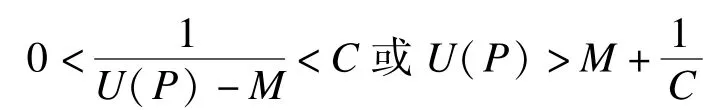
与M为U(P)在[Pmin,Pmax]上的下确界的假设相矛盾,存在Popt∈[Pmin,Pmax],使得U(Popt)=M,即函数U(P)在区间[Pmin,Pmax]内可取得最小值。

(2)U(P)最小值唯一性证明

3 多PE并行优化方法验证

根据灰度共生矩阵和单精度浮点矩阵乘法计算的特点,设计多个PE并行结构,利用本文提出的方法对灰度共生矩阵和单精度浮点矩阵乘法的PE并行结构进行优化,实现运行时间和资源消耗的优化。

3.1 灰度共生矩阵的优化

灰度共生矩阵是研究图像纹理特征的一个有效手段,并广泛应用于生物医学[7-8]、目标检测[9-10]、质量控制[11]和遥感图像分析[12]等领域。

3.1.1 灰度共生矩阵PE的设计

计算灰度共生矩阵的PE如图3所示[13]。因为每个像素对的计算都是相互独立的,从并行计算的角度考虑,可设计多个PE并行完成灰度共生矩阵的计算。

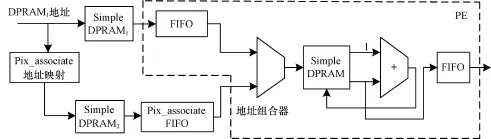
图3 灰度共生矩阵的PE结构

3.1.2 灰度共生矩阵PE资源消耗分析

如图3所示,一个PE中主要包含地址组合器和数据加法器2个功能模块,并且一个PE共有3个16位定点加法器和1个16位定点乘法器等基本逻辑功能单元,其中2个16位定点加法器和1个16位定点乘法器用于实现地址组合器。加法器和乘法器占用slice的数量可用式(10)、式(11)进行计算,其中,M=max(in1(I+F),in2(I+F));I为整数部分的位宽;F为小数部分的位宽。

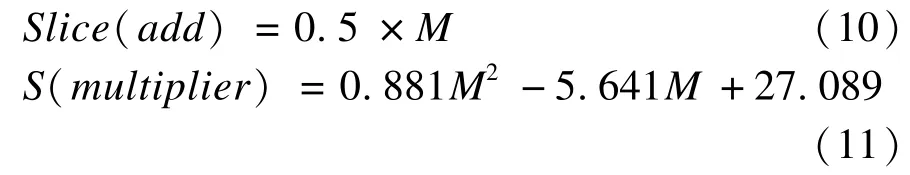
资源消耗随PE的个数P的变化趋势如图4所示,资源消耗会随着PE个数P的增加呈线性增长。

图4 灰度共生矩阵资源消耗随PE个数变化趋势

3.1.3 灰度共生矩阵运行时间分析

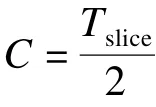
通过式(7)可计算得到P个PE对64×64大小的图像操作的运行时间,运行时间随着PE个数P的变化趋势如图5所示,随着PE数量的增加整个系统的运行时间会越来越小,但由于受到布线延时的影响,当PE数量增加到一定程度后,系统的运行时间会基本保持不变。

图5 灰度共生矩阵运行时间随PE个数变化趋势

3.1.4 灰度共生矩阵运行时间和资源消耗的优化

无量纲化后的运行时间L′(P)、面积消耗T′slice(P)和U(P)随PE的个数P的变化趋势如图6所示。当P=8.45时可实现面积消耗和运行时间的折衷优化。本设计中为了便于计算,要求P应能够被N×N整除,因此,取P=8。

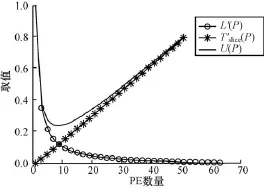
图6 灰度共生矩阵随PE的变化趋势

3.2 单精度浮点矩阵乘法的优化

单精度浮点矩阵乘法的PE采用文献[4]提出的第2种设计方法,一个PE包含1个32位浮点乘法器、1个32位浮点加法器和2个多路复用器等基本功能逻辑单元,其中,浮点加法器和浮点乘法器采用并行和流水线结构设计。设矩阵A、B维数为40×40,将矩阵A分成20×40的2个子模块,将矩阵B分成40× 20的2个子模块,实现浮点矩阵乘法的计算。

3.2.1 单精度浮点矩阵乘法PE资源消耗分析

一个PE共有1个32位浮点乘法器、1个32位浮点加法器和2个多路复用器等基本功能逻辑单元。32位浮点加法器占用slice的数量可用式(13)进行计算,其中,E表示指数位数;M表示尾数位数,也可通过ISE软件综合得到。32位浮点乘法器和多路复用器占用的slice数量由ISE软件综合得到。

Slice(add_FP)=5.40×E+11.06×M+51.20

(13)

结合式(1)可计算得到P个PE的资源消耗,资源消耗随PE的个数P的变化趋势如图7所示,资源消耗会随着PE个数P的增加呈线性增长。

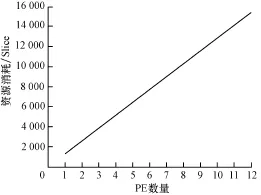
图7 矩阵乘法资源消耗随PE个数变化趋势

3.2.2 单精度浮点矩阵乘法PE运行时间分析

单精度浮点矩阵乘法 PE的逻辑延时Llogic如式(14)所示。布线延时Lrouting直接由布线长度决定,布线长度可由式(3)计算得到。至此,布线延时Lrouting可由式(5)计算得到。

通过式(7)可计算得到P个PE对40×40大小的单精度浮点矩阵乘法的运行时间,运行时间随着PE的个数P的变化趋势如图8所示。随着PE数量的增加整个系统的运行时间会越来越小,但由于受到布线延时的影响,当PE数量增加到一定程度后,系统的运行时间会基本保持不变。

图8 矩阵乘法运行时间随PE个数变化趋势

3.2.3 运行时间和资源消耗优化分析

无量纲化后的运行时间L′(P)、面积消耗T′slice(P)和U(P)随PE的个数P的变化趋势如图9所示。当P=3.42时可实现面积消耗和运行时间的折衷优化。根据文献[4],P应能够被20整除,因此,取P=4,即当P=4时可实现运行时间和资源消耗的优化设计。

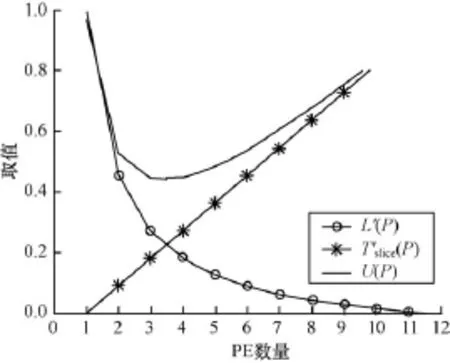
图9 矩阵乘法随PE的变化趋势

4 实验结果与分析

为进一步验证本文提出的方法,将本文提出的计算灰度共生矩阵的方法和计算矩阵乘法的方法在XC5VFX100T上进行实验验证。将灰度共生矩阵的计算方法与文献[14-16]提出的计算灰度共生矩阵的方法分别从运行时间和资源消耗方面进行对比。因为文献[14-16]中并行计算了d={1,2,3,4},θ= {0°,45°,90°,135°}相组合的16个灰度共生矩阵,但是在实际应用中,针对具体图像只计算d,θ的一种组合即可,为了便于和本文方法比较只利用文献提出的方法计算d=1,θ=0°的灰度共生矩阵,从运行时间和资源消耗方面对采用不同数量的PE实现矩阵乘法进行了对比分析。

4.1 资源消耗对比

表1为本文提出的方法与文献[14-16]方法实现灰度共生矩阵计算的资源消耗对比。文献中采用16个PE完成灰度共生矩阵的计算,而本文提出的方法采用了8个PE并行完成对灰度共生矩阵的计算,并且每一个PE有3个加法器和1个乘法器,每个加法器和乘法器都会占用一定的slice。本文方法消耗的 slice数最少,并且本文方法消耗的 slice registers和slice LUT的数量也是最少的。另外与文献[14-15]相比,本文方法没有使用外部存储资源,对片外存储器访问的延时是片内存储器的1个～2个数量级,因此,提高了系统的实时性。表2为采用不同数量的PE实现矩阵乘法的资源消耗情况,随着PE数量的增加会消耗更多的硬件资源。

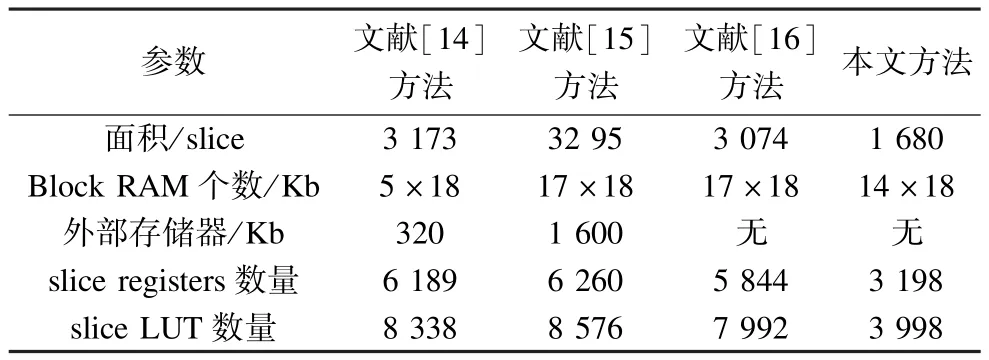
表1 灰度共生矩阵资源消耗对比

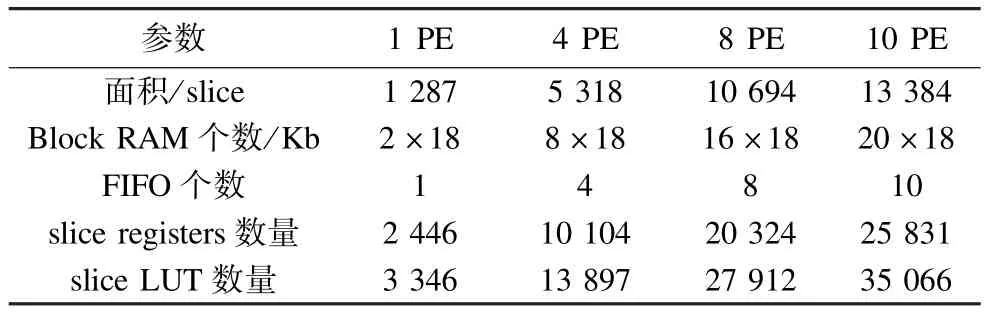
表2 矩阵乘法资源消耗对比

4.2 运行时间对比

图10是在XC5VFX100T上计算图像大小为64×64像素的灰度共生矩阵时各方法运行时间的对比。本文方法计算64×64像素图像的运行时间为76 μs,比文献[14]方法快6.79倍,比文献[16]方法快4.75倍,比文献[15]方法快3.80倍。图11是在XC5VFX100T上采用不同数量的PE计算40×40像素的浮点矩阵乘法的运行时间对比,随着PE数量的增加运行时间逐渐减少,但其减少的幅度越来越小,例如4PE并行时的运行时间比1PE时快3.72倍,而8PE并行时的运行时间为4PE并行时快1.72倍,因为随着PE数量的增加,PE间的通信开销会逐渐增加,布线延时也会随之增加,布线延时的增加会导致运行时间的增加。

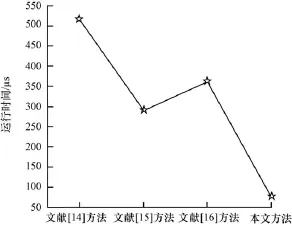
图10 灰度共生矩阵运行时间对比

图11 矩阵乘法运行时间对比

4.3 运行时间和资源消耗综合对比

图12是灰度共生矩阵各种方法中运行时间和资源消耗归一化后的综合对比。与其他方法相比,本文方法的运行时间和资源消耗最小,实现了资源消耗和性能的优化。

图12 灰度共生矩阵运行时间和资源消耗的综合对比

图13是采用不同数量的PE计算矩阵乘法的运行时间和资源消耗的综合对比,利用本文提出的优化方法设计的4PE并行的运行时间和资源消耗最小,实现了资源消耗和性能的优化。

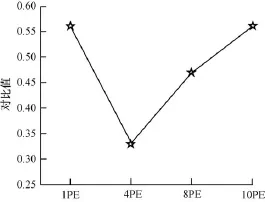
图13 矩阵乘法运行时间和资源消耗的综合对比

5 结束语

本文根据多PE并行中运行时间和资源消耗随PE数量变化的规律,提出了基于运行时间与资源消耗的多PE并行优化方法,利用本文提出的优化方法对灰度共生矩阵和单精度浮点矩阵乘法进行了优化,并将本文提出的灰度共生矩阵并行计算方法与现有的灰度共生矩阵计算方法进行对比,实验结果表明该优化方法可实现多PE并行中运行时间与资源消耗的优化。

由于多PE并行以单PE为基础,因此单PE优化对于系统整体性能的提高具有重要意义,而单PE的内部操作之间具有相关性,这些相关性与实现的具体任务有关,可采用流水线结构进行设计,下一步工作需要对基于运行时间与资源消耗的流水线优化进行研究。

[1] Uzun I S,Bouridance A A A.FPGA Implementations of Fast Fourier Transforms for Real-time Signal and Image Processing[J].Vision,Image and Signal Processing, 2005,152(3):283-296.

[2] Huitzil C T,Estrada M A.Real-time Image Processing with a Compact FPGA-based Systolic Architecture[J]. Real Time Imaging,2004,10(3):177-187.

[3] Dou Yong,Vassiliadis S,Kuzmanov G K,et al.64-bit Floating-point FPGA Matrix Multiplication[C]//Proc.of the 13th International Symposium on Field Programmable Gate Arrays.Monterey,USA:[s.n.],2005:86-95.

[4] Kumar V B Y,Joshi S,Patkar S B,et al.FPGA Based High Performance Double-precision Matrix Multiplication[J]. International Journal of Parallel Programming,2010,38(4):322-338.

[5] Deng Linpeng,Sobti K,Zhang Yuanrui,et al.Accurate Area,Time and PowerModelsforFPGA-based Implementation[J].Journalof SignalProcessing Systems,2011,63(1):39-50.

[6] Nayak A,Haldar M,Choudhary A,et al.Accurate Area and Delay EstimatorsforFPGAs[C]//Proc.of International Conference on Design Automation and Test in Europe.Paris,France,2002:862-869.

[7] Chai H Y,Wee L K,Swee T T,et al.Gray-level Cooccurrence Matrix Bone Fracture Detection[J]. American Journal of Applied Sciences,2011,8(1): 7-16.

[8] Hafizah W M,Supriyanto E,Yunus J.Feature Extraction ofKidney Ultrasound Images Based on Intensity Histogram and Gray Level Co-occurrence Matrix[C]// Proc.of the 6th Asia Modelling Symposium.Bali, Indonesia:[s.n.],2012:115-120.

[9] Gupta M,Bhaskar D,Bera R,et al.Target Detection of ISAR Data by Principal Component Transform on Cooccurrence Matrix[J].Pattern Recognition Letters, 2012,33(13):1682-1688.

[10] Dash A,Kanungo P,Mohanty B P.A Modified Gray Level Co-occurrence Matrix Based Thresholding for Object Background Classification [C]//Proc.of International Conference on Communication Technology and System Design.Tamil Nadu,India:[s.n.],2011: 85-91.

[11] Lu Wenbo,Jiang Weikang,Wu Haijun,et al.A Fault Diagnosis Scheme of Rolling Element Bearing Based on Near-field Acoustic Holography and Gray Level Cooccurrence Matrix[J].Journal of Sound and Vibration, 2012,331(15):3663-3674.

[12] 张绍明,何向晨,张小虎,等.高分辨率星载SAR图像水上桥梁解译[J].电子与信息学报,2011,33(7): 1706-1712.

[13] 郑 红,李 钊,李 俊.灰度共生矩阵的快速实现和优化方法研究[J].仪器仪表学报,2012,23(11): 2509-2515.

[14] Tahir M A,Bouridane A,Kurugollu F,etal.Accelerating the Computation of GLCM and Haralick Texture Features on Reconfigurable Hardware[C]//Proc.of International Conference on Image Processing.[S.l.]: IEEE Press,2004:2857-2860.

[15] Iakovidis D K,Maroulis D E,Bariamis D G.FPGA Architecture forFastParallelComputation ofCooccurrence Matrices [J]. Microprocessors and Microsystems,2007,31(2):160-165.

[16] Sieler L,Tanougast C,Bouridance A.A Scalable and Embedded FPGA Architecture for Efficient Computation of Grey Level Co-occurrence Matrices and Haralick Textures Features [J]. Microprocessors and Microsystems,2010,34(1):14-24.

编辑 顾逸斐

Research on Optimization Method of
Multiple Processing Element Parallelization

LI Zhao,ZHENG Hong
(School of Automation Science and Electrical Engineering,Beihang University,Beijing 100191,China)

The changing of run time and resource consumption with the number of the Processing Element(PE)is contrary.The rules of run time and resource consumption with the number of PE are analyzed.And the variation trend for resource consumption and run time with the number of PE is got.The optimization objective function based on run time and resource consumption is established.The existence and uniqueness of the minimum for optimization objective function are proved.The multi-PE optimization method based on run time and resource consumption is proposed.This method can realize the run time optimization with the least resource consumption.In order to validate the method,the optimal design of the calculation of the gray level co-occurrence matrix and single float matrix multiplication are proposed.Experimental results indicate that the runtime of gray level co-occurrence matrix is at most 6.79 times than the old method.The integrated result about runtime and area consumption is 3.3 times than the old method.The optimization of runtime and area consumption is implemented.

multiple Processing Element(PE)in parallel;optimization method;runtime;area consumption;gray level co-occurrence matrix;single float matrix multiplication

1000-3428(2014)09-0305-07

A

TP316

10.3969/j.issn.1000-3428.2014.09.061

国家自然科学基金资助项目(60543006);博士点基金资助项目(201003259);光电信息重点实验室基金资助项目(9140 C150105100C1502)。

李 钊(1983-),男,博士研究生,主研方向:并行计算,嵌入式系统设计;郑 红,教授。

2013-07-01

2013-08-28E-mail:lizhao_buaa@126.com