基于数字图像分割法的跨孔雷达走时层析成像

曲昕馨，李桐林，王 飞

吉林大学地球探测科学与技术学院，长春 130026

基于数字图像分割法的跨孔雷达走时层析成像

曲昕馨，李桐林，王 飞

吉林大学地球探测科学与技术学院，长春 130026

跨孔雷达走时层析成像主要利用雷达波的走时进行反演，走时提取的正确与否将直接影响到层析成像的效果。数字图像分割法基于凸集投影（POCS）方法，使用能量比彩色图像分割技术准确提取走时。数字图像分割法提取走时首先应用在折射地震波的数据处理中。笔者首次将数字图像分割法提取走时的方法应用到跨孔雷达走时层析成像中，使用迭代线性反演算法重建了雷达波速度场。反演过程中，使用最小二乘QR分解法（LSQR）求解线性方程组，利用弯曲射线追踪技术构建雅可比矩阵，走时的计算值则由多模板快速推进算法（MSFM）得到。为了验证数字图像分割法在走时层析成像中的效果，使用一组合成数据及一组实测数据分别对比了基于数字图像分割法和基于传统能量比法获得的层析成像反演结果。对比结果表明，使用数字图像分割法得到的层析成像结果更为精确，误差更小，能为判断地下雷达波速度场提供更为有力的帮助。

跨孔雷达；走时提取；走时层析成像；数字图像分割法；凸集投影

0 引言

跨孔雷达走时层析成像是近年来非常流行的一种雷达数据反演方法，被广泛地应用在水文［1］、环境［2］、岩土工程［3］和金属矿探测［4］等领域。影响跨孔雷达走时层析成像的因素有很多，包括射线覆盖角度、正则化因子、测量装置排布以及走时提取等［5］。跨孔雷达走时层析成像主要是利用雷达波的走时进行反演，因此，走时提取的正确与否将直接影响到层析成像的效果。

直达波走时的提取首先是用于地震记录的编辑与处理。传统的走时拾取方法主要分为两大类：一类是基于地震记录瞬时特征的方法，其中最具代表性的是Coppens［6］于1985年提出的能量比法，这类方法对噪声比较敏感，当地震记录的噪声较严重时，走时拾取的精度会受到影响；另一类方法是基于地震记录整体特征的方法，其中最常见的是相关法［7］，这类算法虽然对噪声有较好的抑制作用，但受到地震道之间相似性等因素的影响，对于复杂地震记录，难以准确拾取走时。因此，研究者们又相继提出了一些改进算法。如Al-Ghamdi［8］通过使用自适应阈值改进了Coppens的方法，Sabbione等［9］使用熵和分维方法改进了Coppens的方法等。

在钻孔雷达走时层析成像中，走时提取技术的研究发展得比较晚。Messinger［10］将互相关方法与STA/LTA（信号短时平均值/信号长时平均值）技术相结合来自动拾取走时；Irving等［11］将互相关方法应用到共射线角度集记录的直达波走时的提取中；Tronicke［12］提出了一种基于统计标准的走时提取方法；Bernard等［13］提出了一种使用赤池信息准则和连续小波变换进行走时提取的方法。

笔者将一种新的走时提取方法——数字图像分割法应用到跨孔雷达走时层析成像中。数字图像分割法由Mousa提出，是Coppens方法的一种改进算法，最初应用在折射地震波数据的走时提取中。该方法使用基于凸集投影（POCS）［14］的能量比彩色图像分割技术准确提取走时［15］。为了验证该方法在走时层析成像中的效果，笔者使用一组合成数据及一组实测数据分别对比基于数字图像分割法和基于传统能量比法获得的层析成像反演结果。在反演算法上，选取常用的迭代线性反演算法［16］，并使用最小二乘QR分解法（LSQR）［17］求解线性方程组。反演过程中雅可比矩阵的构造由弯曲射线追踪技术［18］实现，走时的计算值由多模板快速推进算法（MSFM）［19］得到。

1 数字图像分割法提取走时

数字图像分割法的分割是在能量比图像上进行的。由于走时的能量比通常比后续波的能量比高，可以在索引颜色图上为它们分配不同的颜色。一旦获得包含走时的分割后的图像（走时被分配一个参考颜色），可以很容易地将可能走时位置的索引从能量比图像上映射到它们对应的雷达记录上。按照Coppens［6］的方法，计算能量比时，首先需要分别计算一个滑动窗口以及一个累积窗口内的能量，然后将滑动窗口内的能量与累积窗口内的能量相比。滑动窗口的长度为L，累积窗口的长度为从初始采样点开始一直到当前滑动窗口位置。能量比的公式如下：

式中：ERj是从第j个采样点开始的能量比的值；Ai是第i个采样点的信号振幅。

数字图像分割法使用POCS技术进行图像分割。POCS技术的基本思路是：给定一个参考颜色向量r，希望寻找到所有的颜色向量h∈I⊆H（I是给定希尔伯特空间H的一个子集的图像），受限于一定的限制条件Ci∈H。对于m个已知的属性，则有m个限制条件。h可以由联立的POCS公式迭代求解获得：

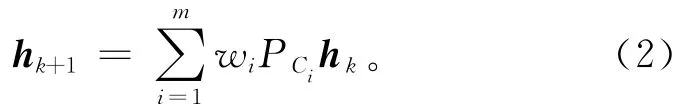
可以施加如下定义的限制条件：

式中：ε是h和r之间的最大距离；ρ是一个相关系数，满足0≤｜ρ｜≤1；C1和C2在H中分别表示一个球体和一个圆锥体，因此它们都是凸集。在数字图像分割法中，所需要的解的集合为这2个凸集的交集。基于公式（3）和（4）的拉格朗日公式，使用紧邻原则，可以推导出公式（3）和（4）对应的相关投影算子公式：

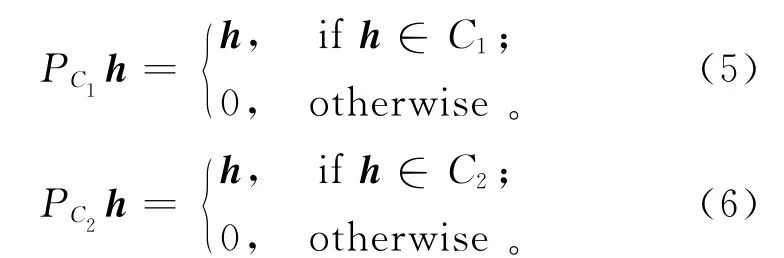
下面给出基于POCS技术的数字图像分割法的具体实现步骤：

1）对于一个给定的雷达数据集，首先使用公式（1）计算其能量比振幅。

2）将每个振幅分配一个索引颜色。

3）将这些能量比索引颜色转换到一个3D像素颜色域（例如RGB域），可以得到一个彩色的能量比数字图像。对于低信噪比的数据，还可以对能量比图像使用中值滤波进行预处理以增强图像质量。

4）选择w1、w2、ε和ρ的值。

5）在能量比图像中选取走时所对应的参考颜色r。

6）使用公式（2）、（5）和（6）计算满足公式（3）和（4）的向量h。

7）如果hk＋1和hk之间的误差小于一个给定的阈值，则停止；否则，重复步骤4）至6）。

8）分割后走时区域的下缘的索引即为走时的位置。

2 基于弯曲射线追踪的走时层析成像算法

笔者使用Tikhonov正则化函数［20］作为走时层析成像反演的总目标函数：

式中：tmes和tc（s）分别为走时的观测值（即提取的走时）和计算值；s和s0分别为待求的慢度向量和初始模型的慢度向量；Wd和Wm分别为数据加权矩阵和模型加权矩阵［21］；λ是正则化参数。最小化φ（s），可以推导出：

式中，J＝∂t∕∂s是雅可比矩阵，它由每个慢度元胞内的走时对慢度的偏导数组成。走时函数tc（s）取决于未知的慢度s，所以tc（s）是非线性的。为了获得tc（s）的近似线性形式，对tc（s）进行泰勒级数展开，并且只保留一阶项，tc（s）可以近似表示成tc（s）≈tc（s0）＋Js0（s－s0）。此时，式（8）变成：

为了提高反演的精度，使用迭代线性反演公式将式（9）写成如下的迭代形式：

求解式（10）需要进行矩阵与矩阵的相乘，非常耗时间。一个更好的算法是寻找下式的最小二乘解［22］：

式（11）的解比（10）的解精确得多，并且具有更高的计算效率。笔者使用LSQR算法［17］求解式（11）。走时的观测值tmes通过数字图像分割法进行走时提取得到，走时的计算值tc（sk）则使用高精度的MSFM 算法［19］计算求得。弯曲射线追踪算法［18］则被用来精确地追踪射线路径和构建雅可比矩阵Jk。

3 合成数据实例

为了验证数字图像分割法在跨孔雷达走时层析成像中的反演效果，首先使用数字图像分割法对合成数据模型的数值模拟结果进行走时提取，并使用提取的走时进行层析成像反演。如图1所示，合成数据模型为高11m、宽6m的随机介质模型，采用二维时域有限差分（FDTD）算法对该模型进行数值模拟。发射天线和接收天线分别布设在距模型左边界0.5m和右边界0.5m的2个钻孔中。发射天线从0.5m深度处开始移动，每次移动0.25m，共移动41次；对于每个发射天线位置，接收天线都从0.5 m深度处开始布设，每隔0.25m布设一个接收天线，每个发射天线对应41个接收天线。这样，整个模型区域共有1 681条射线。

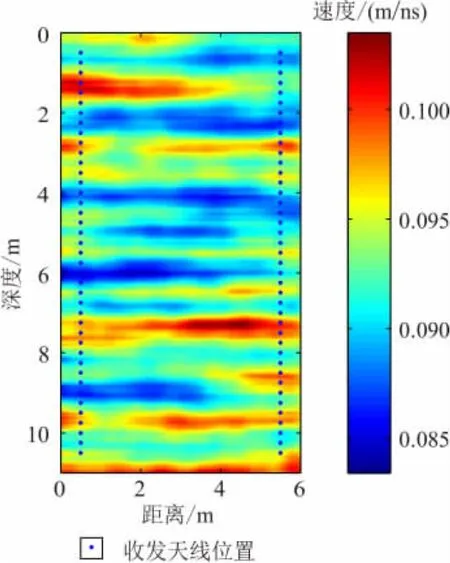
图1 用来生成合成数据的随机介质模型Fig.1 The random medium model used to generate synthetic data set

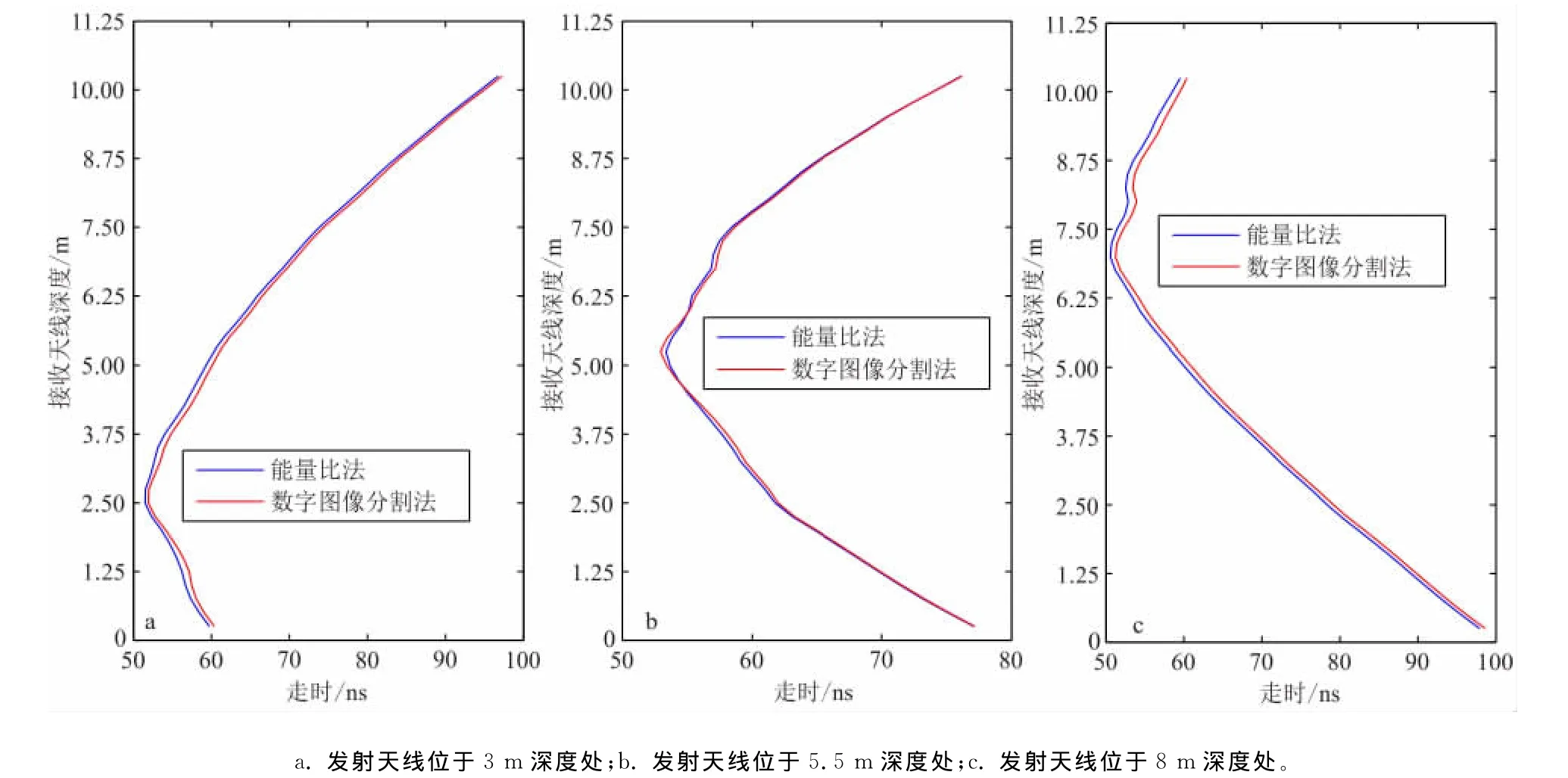
图2 合成数据提取的走时Fig.2 The extracted traveltimes of synthetic data set

图2为由数值模拟得到的合成数据的某几道分别使用能量比法和数字图像分割法提取的各条射线的走时对比。从图2中可以看出，2条曲线的整体趋势比较相似，但部分位置还是存在一定差异，尤其在各发射天线位置附近差异最大。这说明这2种方法提取的走时会使得两者的反演结果在发射天线位置（即左侧钻孔处）产生较大的不同。至于这2种提取方法哪种更准确，由于随机介质模型的理论走时无法获得，很难进行对比。但是，可以将这2种方法提取的走时应用到走时层析成像反演中，通过对比反演结果的误差而从一个侧面来判定这2种方法提取走时的精确性。

层析成像反演时，初始模型选取为一个速度为0.1m/ns的均匀介质模型，反演网格距为0.05m，Wd和Wm分别选取单位矩阵和拉普拉斯算子。正则化参数λ的值选为25。为了测量反演后的速度模型接收天线处走时的计算值tc（sk）与提取的合成数据模拟结果的走时tmes之间的误差，笔者使用了均方根误差（RMS）：

式中，n为总射线数。

图3a为基于能量比法提取的走时进行的层析成像反演结果。可以看出，反演的结果较好，但是在靠近层析成像图的左侧钻孔的位置，反演出了很多原模型中并不存在的虚假异常。如在0.5、5、6和10.5m深度处均出现了比较明显的虚假异常，这与图2中2条走时曲线的最大差异处吻合得很好。图3b为基于数字图像分割法提取的走时进行的层析成像反演结果。图3b与图3a大体上很相似，但是图3a中出现的虚假异常在图3b中均没有出现，并且图3b的均方根误差（0.06ns）明显小于图3a（0.13ns）。这说明，相比于能量比方法，数字图像分割法提取的走时更加准确，并且基于数字图像分割法所得到的层析成像反演结果精度更高，更加接近真实模型。

图3 合成数据模型反演结果Fig.3 The reconstructed results of synthetic data set

4 实测数据实例

使用一组实测数据来评价基于数字图像分割法的跨孔雷达走时层析成像方法的反演效果。该实测数据采自贵州。贵州位于我国西南地区，地下广泛分布着可溶性的碳酸盐岩（灰岩、白云岩等），介电常数约为9（电磁波速度约为0.1m/ns）。由于该地区岩溶作用明显，其地下多分布裂隙和溶洞。部分裂隙和溶洞中由于水的存在，其介电常数明显增大，平均介电常数为14～18（电磁波速度为0.07～0.08 m/ns）；部分裂隙和溶洞中充满空气，使得其介电常数相对周围围岩（碳酸盐岩）明显减小（电磁波速度相应增大）。因此，可以通过观察跨孔雷达走时层析成像的结果来判断该地区地下溶洞和裂隙的分布情况及性质（含水或是含空气）。

在数据采集过程中，2个钻孔之间的水平距离为18m，垂直方向上的测量区域为5.6～48.0m。发射天线在左侧钻孔9～48m深度之间移动，每次移动1m。接收天线在右侧钻孔5.6～47.2m深度范围内，每隔0.2m布设一个。反演中网格距为0.2m，其他参数与合成数据实例中的参数一致。

图4为分别使用能量比法和数字图像分割法对实测数据提取的发射天线位于某些深度处的走时。可以看出，两者的差异还是比较大的。从整体上来看，各深度能量比法提取的走时几乎都大于数字图像分割法提取的走时。并且图4b中还能观察到能量比法提取的走时在某些位置上还存在着较大的突变；这是因为实测数据的某些道信噪比不高，而能量比法在处理低信噪比数据时会产生很大误差。但是这些突变在数字图像分割法提取的走时曲线中并没有出现，说明数字图像分割法在数据信噪比较低的情况下仍能获得较高的走时提取精度。

图5a和图5b分别为基于能量比法和数字图像分割法所提取的走时进行层析成像的反演结果。

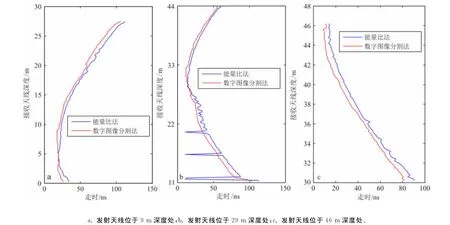
图4 实测数据走时Fig.4 The extracted traveltimes of field data set

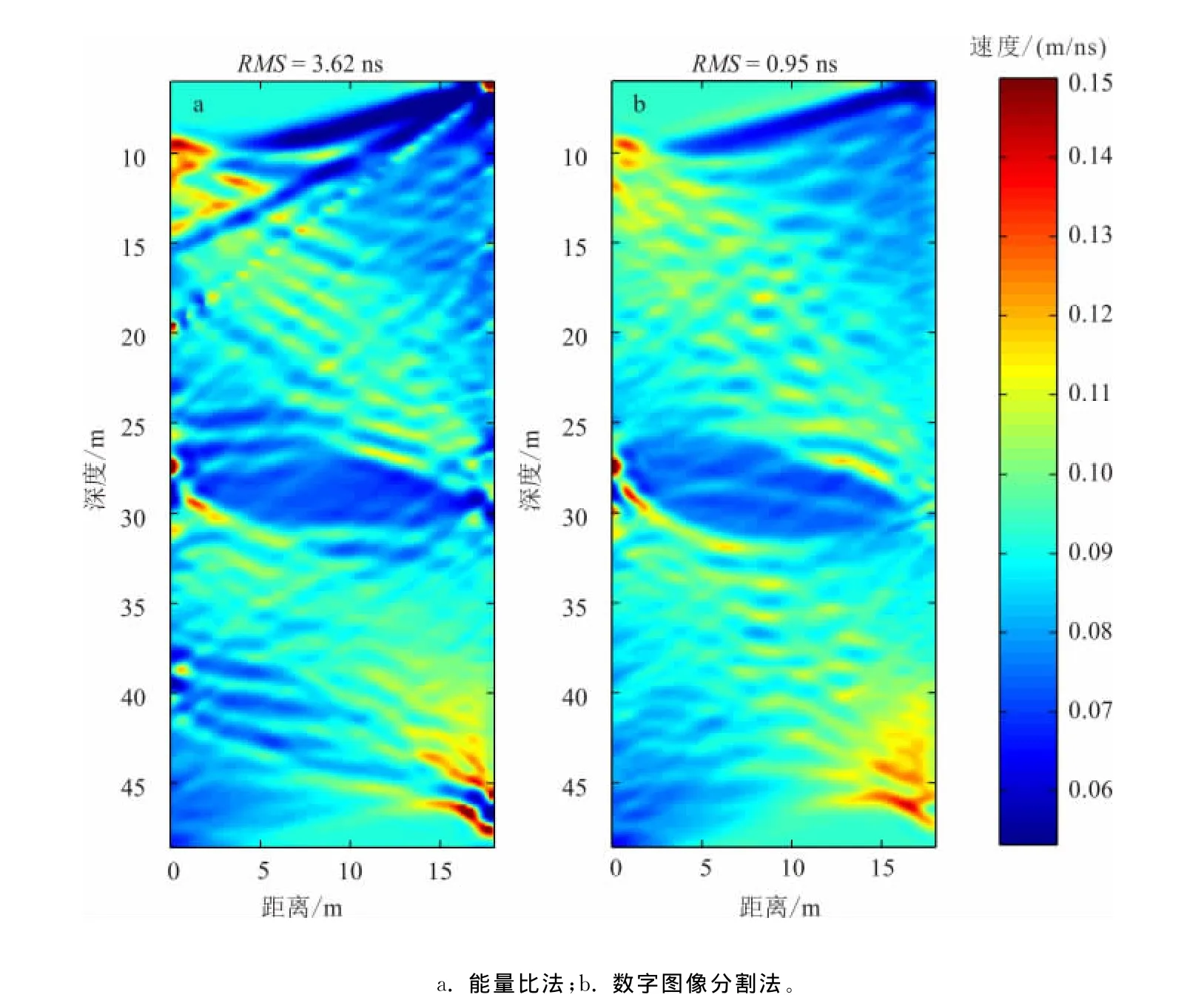
图5 实测数据模型反演结果Fig.5 The reconstructed results of field data set

可以看出：图中最主要的异常为25～30m深度处的一个水平低速层（图中用蓝色表示），该低速层的电磁波速度为0.07～0.08m/ns，与含水溶洞对应得很好，因此可判断该低速层为一含水溶洞；此外，图5a和图5b的右上角和左下角均分布零星的低速体（蓝色区域），可以推断出这2个位置也分布着一些小型的含水裂隙；而在两图的左上角和右下角，则分布着一些条带状的高速体，结合当地的地质背景，可以推断其为一些含空气的裂隙。图5中在11～40m处的那些较小的异常为虚假异常，是由于发射天线移动步长较大而引起的射线覆盖较稀疏造成的。

图5a和图5b的区别主要体现在2个地方：一是图5a在5～15m范围内有一条倾斜的蓝色低速带，而图5b中则没有；二是图5a的右下角在2条高速带（红色）之间出现了一条低速带（蓝色），而图5b中的相应位置同样没有。可以认为这些异常为虚假异常，推测是图4b中所示的那些走时曲线突变造成的，这已被后期的钻探结果证实。此外，通过对比图5a和图5b可以看出，图5b对背景场的重建更加光滑，虚假异常更少一些。在反演误差上，基于数字图像分割法反演结果的误差（0.95ns）要远远小于基于能量比法反演结果的误差（3.62ns）。这说明，对于实测数据，基于数字图像分割法所提取的走时的反演结果也好于基于能量比法所提取的走时的重建结果。

5 结论

1）合成数据模拟结果表明，基于数字图像分割法提取的走时精度高于基于能量比法所提取的走时精度，数字图像分割法具有更高的抑制干扰的能力。

2）通过对模型数据与实测数据反演结果的分析，可以发现基于数字图像分割法能获得远远好于基于能量比法的层析成像反演结果。它能够减少发射天线附近以及信噪比较低情况下所产生的虚假异常，从而获得更好的速度场重建结果。

总之，无论对于合成数据还是实测数据，使用数字图像分割法得到的层析成像结果更为精确，误差更小，能为判断地下雷达波速度场提供更为有力的帮助。

（References）：

［1］Tronicke J，Holliger K，Barrash W，et al.Multivari-ate Analysis of Cross-Hole Georadar Velocity and Attenuation Tomograms for Aquifer Zonation［J］.Water Resources Research，2004，40（1）：W01519.

［2］Gloaguen E，Marcotte D，Giroux B，et al.Aubertin，Stochastic Borehole Radar Velocity and Attenuation Tomographies Using Cokriging and Cosimulation［J］.Journal of Applied Geophysics，2007，62（2）：141-157.

［3］Johnson T C，Routh P S，Barrash W，et al.A Field Comparison of Fresnel Zone and Ray-Based GPR Attenuation-Difference Tomography for Time-Lapse Imaging of Electrically Anomalous Tracer or Contaminant Plumes［J］.Geophysics，2007，72（2）：21-29.

［4］刘四新，周俊峰，吴俊军，等.金属矿钻孔雷达探测的数值模拟［J］.吉林大学学报：地球科学版 ，2010，40（6）：1479-1484.

Liu Sixin，Zhou Junfeng，Wu Junjun，et al.Numerical Simulations of Borehole Radar for Metal Ore Detection［J］.Journal of Jilin University：Earth Science Edition，2010，40（6）：1479-1484.

［5］冉利民，刘四新，李玉喜，等.影响跨孔雷达层析成像效果的几个因素［J］.吉林大学学报：地球科学版，2013，43（5）：1672-1680.

Ran Limin，Liu Sixin，Li Yuxi，et al.Several Factors Affecting Cross-Hole Radar Tomography［J］.Journal of Jilin University：Earth Science Edition，2013，43（5）：1672-1680.

［6］Coppens F.First Arrival Picking on Common-Offset Trace Collections for Automatic Estimation of Static Corrections［J］.Geophysical Prospecting，1985，33（8）：1212-1231.

［7］Molyneux J B，Schmitt D R.First-Break Timing：Arrival Onset Times by Direct Correlation［J］.Geophysics，1999，64（5）：1492-1501.

［8］Al-Ghamdi A.Automatic First Arrival Picking Using Energy Ratios［D］.Saudi Arabia：King Fahd University of Petroleum ＆ Minerals，2007.

［9］Sabbione J I， Velis D. Automatic First-Breaks Picking：New Strategies and Algorithms［J］.Geophysics，2010，75（4）：67-76.

［10］Messinger J.Effective Automatic Picking of Traveltime Data with High Precision［C］//Slob E，Yarovoy A，Rhebergen J.Proceedings of the 10th International Conference on GPR.Delft：Delft University of Technology，2004：91-94.

［11］Irving J D，Knoll M D，Knight R J.Improving Crosshole Radar Velocity Tomograms：A New Ap－proach to Incorporating High-Angle Traveltime Data［J］.Geophysics，2007，72（4）：31-41.

［12］Tronicke J.The Influence of High Frequency Uncorrelated Noise on First-Break Arrival Times and Crosshole Traveltime Tomography［J］.Journal of Environmental and Engineering Geophysics，2007，12（2）：173-184.

［13］Bernard G，Abderrezak B，Michal C.Assisted Travel-Time Picking of Crosshole GPR Data ［J］.Geophysics，2009，72（4）：35-48.

［14］Gubin L G，Polyak B T，Raik E V.The Method of Projections for Finding the Common Point in Convex Sets［J］. USSR Computational Mathematics and Mathematical Physics，1967，7（6）：1-24.

［15］Mousa W A，Al-Shuhail A A，Al-Lehyani A.A New Technique for First-Arrival Picking of Refracted Seismic Data Based on Digital Image Segmentation［J］.Geophysics，2011，76（5）：79-89.

［16］Pelton W H，Rijo L，Swift C M.Inversion of Two-Dimensional Resistivity and Induced-Polarization Data［J］.Geophysics，1978，43（4）：788-803.

［17］Paige C C，Saunders M A.LSQR：An Algorithm for Sparse Linear Equations and Sparse Least Squares［J］.ACM Transactions on Mathematical Software，1982，8（1）：43-71.

［18］Aldridge D F，Oldenburg D W.Two-Dimensional Tomographic Inversion with Finite-Difference Traveltimes［J］.Journal of Seismic Exploration，1993，2（3）：257-274.

［19］Hassouna M S，Farag A A.Multistencils Fast Marching Methods：A Highly Accurate Solution to the Eikonal Equation on Cartesian Domains［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2007，29（9）：1-12.

［20］Tikhonov A N，Arsenin V Y.Solution of Ill-Posed Problems［M］.Washington：Winston ＆Sons，1977.

［21］Greenhalgh S A，Bing Z，Green A.Solutions，Algorithms and Inter-Relations for Local Minimization Search Geophysical Inversion［J］.Journal of Geophysics and Engineering，2006，3（2）：101-113.

［22］Lines L R，Treitel S.Tutorial：A Review of Least-Squares Inversion and Its Application to Geophysical Problems［J］.Geophysical Prospecting，1984，32（2）：159-186.

Cross-Hole Radar Travel-Time Tomography Based on Digital Image Segmentation

Qu Xinxin，Li Tonglin，Wang Fei

CollegeofGeoExplorationScienceandTechnology，JilinUniversity，Changchun130026，China

The effectiveness of cross-hole radar tomography depends mainly on the quality of the extracted first arrival-time.Digital image segmentation method，based on the projection onto convex sets（POCS）technique，is used to extract the first arrival-time by segmenting the color image of the energy ratio，and had previously been applied in refracted seismic first arrival-time extraction.We first applied digital image segmentation method into cross-hole radar travel-time tomography to reconstruct the velocity field using an iteratively linearized inversion approach.During the inversion，LSQR algorithm was employed to solve the system of linear equations，Jacobian matrix was constructed by the curved ray tracing technique，and the travel-time was calculated using Multistencils Fast Marching Method（MSFM）.We employed a synthetic data set and a field data set to test the effectiveness of the digital image segmentation method in travel-time tomography.For comparison，a traditional energy ratio method is also used for first arrival-time extraction.The result reflected that the tomography based on digital image segmentation method is more accurate with smaller residuals，and can provide more effective judgment for the underground velocity field.

cross-hole radar；first arrival-time extraction；travel-time tomography；digital image segmentation；projection onto convex sets

10.13278/j.cnki.jjuese.201404302

P631.2

A

曲昕馨，李桐林，王飞.基于数字图像分割法的跨孔雷达走时层析成像.吉林大学学报：地球科学版，2014，44（4）：1340-1347.

10.13278/j.cnki.jjuese.201404302.

Qu Xinxin，Li Tonglin，Wang Fei.Cross-Hole Radar Travel-Time Tomography Based on Digital Image Segmentation.Journal of Jilin University：Earth Science Edition，2014，44（4）：1340-1347.doi：10.13278/j.cnki.jjuese.201404302.

2013-11-11

国家重大科学仪器设备开发专项（2011YQ05006009）；中国地质调查局吉黑东部综合找矿方法研究项目（12120113098400）

曲昕馨（1984—，女，博士研究生，主要从事电磁法正反演研究，E-mail：xinxin2191＠sina.com

李桐林（1962—，男，教授，博士生导师，主要从事电磁法理论及其应用的研究，E-mail：lilaoshizh＠163.com。