导线测量平差方法的探讨

郭军鹏

(山西省公路局晋城分局，山西晋城 048000)

1 概述

随着全站仪在公路行业的普及使用，导线测量因其灵活的布线方式、良好的地形适应性和简单易操作的特点，普遍以全站仪测导线的方式用于控制网的加密和二级、三级及以下公路平面控制网的建立。但随之出现了一些不符合规范及平差基本要求的看似正确简单的平差方法。

2 问题的提出

近年来在全站仪测导线的平差中，出现了一种“坐标近似平差法”。这种方法依托全站仪可以通过机内的微处理机，直接得到地面点的平面坐标的特点，采用以下步骤来进行导线点坐标平差。

导线具体计算如图1所示。

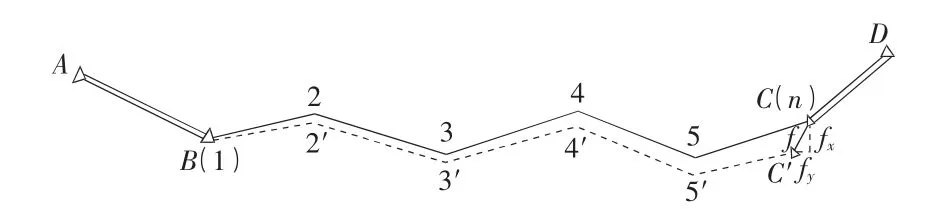
图1 导线计算示意图

1)计算导线坐标闭合差f。

由于存在测量误差，最后测得的C点坐标不等于C点的已知坐标，平面位置产生一缺口C'C，即导线全长闭合差f。f在纵、横坐标轴上的投影为纵、横坐标闭合差fx，fy。显然:

其中，x'c，y'c均为C'点的坐标观测值;xc，yc均为C点的已知坐标。

2)计算各点坐标改正值。

各点坐标改正值为:

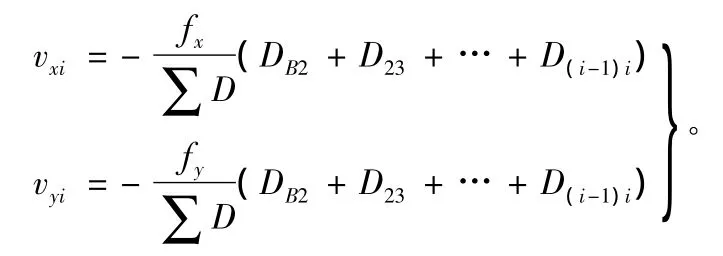
其中，vxi为纵坐标改正值;vyi为横坐标改正值;D为边距;fx为纵坐标闭合差;fy为横坐标闭合差。

3)计算改正后各点坐标。

改正后各点坐标为:

其中，x'i，y'i均为各点坐标的观测值。

以上所述方法，解决了C'C之间的差值，起到了所谓“平差”的效果，但笔者认为值得商榷。

将图1导线，附已知条件及实测值如表1，表2所示。

∠5CD=129°28'22″。

表1 已知点X，Y坐标值m

表2 待定点X，Y坐标值 m

测角中误差2'，测边中误差为msi=±(3 mm+2 ppm·s)。

表3 各点间距表 m

表4 闭合差分配表 m

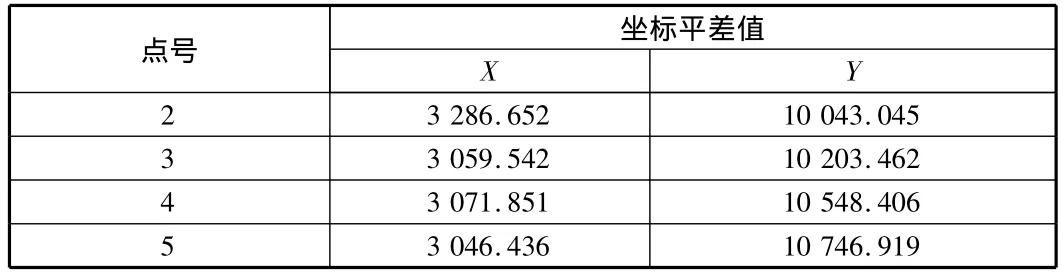
表5 坐标平差改正结果

3 与规范的导线测量近似平差法的比对

导线测量的近似平差步骤为:1)按已知坐标反算计算已知坐标方位角αAB。2)按照观测顺序，计算各条边的坐标方位角，由坐标方位角还原计算出各夹角观测值;由5C'的坐标方位和5C'D之间的角度观测值计算α'CD，计算方位角闭合差fβ=α'CD－αCD。3)分配闭合差，重新依次推算各边的坐标方位角。4)计算各边的坐标增量。5)计算与调整坐标增量闭合差。6)计算各导线点坐标。

按照上述步骤，对前述导线解算为:

1)按前述条件计算为:角度闭合差的分配与计算(见表6)。

表6 角度闭合差分配与计算表

3)解算改正后间距见表7。

表7 解算改正后间距表

4)得改正数见表8。

表8 改正数结果表

5)得改正结果见表9。

表9 改正结果表

该方法与“坐标近似平差法”相比，有以下不同:多了前三个步骤的较复杂计算，但通过观察，前三步正是角度闭合差的调整过程，正是对角度测量的评价和平差处理。通过对步骤2)的详细比对，方法一中没有用到5C'D之间的角度观测值，实质是没有进行方位角的附合，违反了附合导线的基本定义。

可见，方法一角度观测值的处理上是有缺陷的，且偏离了附合导线的基本定义。

4 与经典平差方法的比对

单独对以上两种方法比对，无法确定正误，将其分别与经典法对照如下。所谓经典平差方法，就是在考虑观测值函数模型的同时，考虑观测值的随机模型，在建立观测值函数模型的同时，建立以最小二乘法为基础的随机模型，通过两个模型的联合解算，得到有唯一解的最优结果。具体到附合导线测量，在综合考虑实现及解算难易程度，本文以间接平差法为例简要介绍。间接平差法通过选定T个独立参数，将每个观测量分别表达成这T个参数的函数，建立函数模型。具体为将待测点坐标改正数定为独立参数，用其表达观测值及其改正数，即:

按最小二乘法要求，其随机模型为:

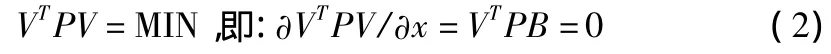
综合式(1)，式(2)，得 BTPBx－BTPl=0。

解算上式，即可得坐标改正数的最优解。

主要计算过程为:

1)列立角误差方程式。设A，B，C三点组成以B为顶点的角，则:

将前述两式按泰勒公式展开，得角误差方程式为:

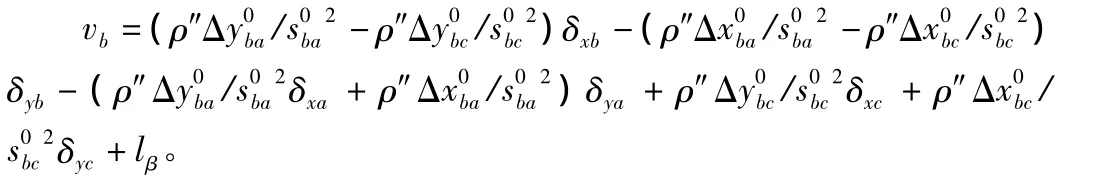
2)列立边误差方程式。由A，B两点坐标反算AB长度为:

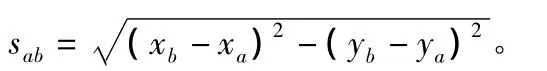
将其表达为误差方程形式并线性划为:

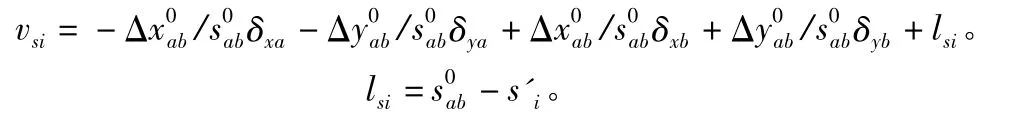
取坐标观测值为近似值，则lsi=0。

其他各符号意义与角误差方程相同。

3)确定权阵。对导线测量而言，观测值为角度与距离，因为观测值相互独立，所以各观测量的权相互独立。一般选取仪器标定精度表示测角与测距中误差，且以测角中误差代表单位权中误差，即测角值权为1，测边值权为

4)解算法方程，得坐标改正值，完成平差。按照上述步骤，代入同样的起算数据，得误差方程的系数阵见表10。

表10 误差方程系数阵表

权阵见表11。

表11 权阵表

计算结果见表12。

表12 改正数计算结果表

改正后坐标见表13。

表13 坐标平差改正后结果

5 结语

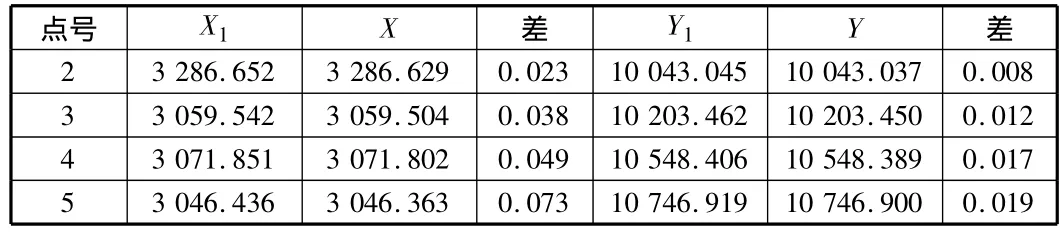
表14 方法一与严密平差比对结果

表15 方法二与严密平差比对结果

方法一，方法二与严密平差比对结果见表14，表15。

可见，方法一与严密平差法的比对中，呈现出明显的规律性，显然存在系统误差，顾及与方法二的比对过程，进一步明确了方法一没有进行角度平差在平差结果中造成的系统性影响，其与平差的基础出发点相悖，同时，方法一的误差绝对值偏大，显然没有达到理想平差效果。故方法一用于附合导线平差是错误的做法。

［1］国家技术监督局.中华人民共和国建设部工程测量规范［M］.北京:中国计量出版社，1993.

［2］武汉测绘科技大学测量平差教研室.测量平差基础［M］.第3版.北京:测绘出版社，1996.