基于Matlab的股票市场收益率波动分析实验

丛 超，徐德玲，庞世达，孙凯旋

基于Matlab的股票市场收益率波动分析实验

丛 超，徐德玲，庞世达，孙凯旋

（重庆理工大学 电子信息与自动化学院，重庆 400054）

针对金融风暴背景下的股票市场价格的波动特性，应用数学分析、经济统计与计量知识，对中国上海、深圳股票综合指数2007～2009年的数据进行实验分析，并利用Matlab金融分析工具箱以及广义自回归异方差模型编程建模，实现对股票市场收益率的分析和预测。结果表明，股票市场收益率序列的波动有显著的异方差性。

股票市场；时间序列分析；广义自回归异方差模型；Matlab编程

金融时间序列收益率的波动是动态变化的，不同金融市场的波动还存在波动溢出。股票作为一种重要的金融产品，其价格行为理论是整个市场金融理论的基础，股市价格行为（behavior of stockmarket prices）一词最早由Fama提出［1］，其核心含义是指股价的行为方式，即变动规律。人们对股票预测也提出了各种不同的方法［2］，从最初的图表分析、技术指标（成交量曲线图、K线图、移动平均线等），到建立数学模型的方法等。随着经济学、数学以及计算机科学的发展，针对金融市场时间序列进行统计性的建模与分析已经成为一项跨学科的分析课题，成为国内外研究的重要方向。

本文通过Matlab编程建立模型，针对2007年1月1日到2009年12月31日中国上海、深圳股票综合指数数据进行实验分析。首先，利用Matlab金融工具箱对股票市场的收益率曲线进行计算，并检验金融分指数序列的平稳性与波动性；其次，通过使用自相关（auto correlation function，ACF）和偏相关（partial auto correlation function，PACF）分析的方法检验序列的自相关性；随后，采用Q检验和自回归异方差检验（auto regressive conditional heteroskedasticity，ARCH）进行平稳性的验证，并使用GARCH（1，1）模型对收益率曲线进行建模分析；最后，本文对模型的优缺点进行了评价，并给出了推广与改进的建议。

1 基本概念

1.1 一般时间序列的统计特性

对于一般的时间序列，主要的统计特征量有以下三种［3］。

1）均值函数

2）自协方差函数

式中：当t=s时，γt，t为时间序列的方差，如下式所示。

3）自相关函数

可用上述三种特征来分析一个时间序列的基本特性，如平稳性检验［4］、正态性、独立性等。

除此之外，在实验中通常还会用到以下几种类型的特性，用于支持或细化分析时间序列建模。

1）样本峰度，用于度量时间序列偏离某分布的情况［5］。例如，正态分布的峰度为3。

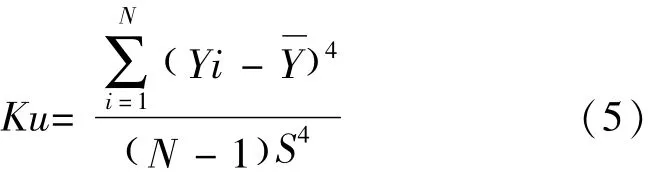
2）样本偏差，用于衡量时间序列的对称性。若偏差为负，则均值左侧的离散度比右侧高，反之亦然。

1.2 股票指数时间序列的特征及建模方法

股票指数作为时间序列的一种，除了具有时间序列的特性之外，本身有着金融产品的特殊性。

1）非平稳性。通常来说，股票指数的时间序列是非平稳的，通过对股票指数的三大时间序列特征的分析，可以很容易得到股票指数序列具有非平稳的特性。

2）收益率序列具有波动聚集性。早在20世纪60年代，Fama针对股市价格行为分析得出结论，在某一段时间内，收益率序列存在持续偏高或偏低的情况，这就是波动聚集性。

3）收益率序列具有异方差性。异方差性指的是针对时间序列进行经典回归分析时，随机误差项μt由于金融产品容易受到随机因素的影响，比如政策变动、自然灾害或金融危机等，同时，人的不确定的社会行为也会对股票指数序列造成影响。因此，针对金融产品的分析通常不能忽视异方差性。

在早些时候，学者对股票价格时间序列的建模大多为几何布朗运动模型［6］。这种建模方法的主要缺陷在于，难以解释股指时间序列具有方差时变、波动集群的特征。而股票指数序列本身具有非平稳性，许多传统的时间序列建模方法就很难应用在股票指数上。

1.3 GARCH模型的基本概念

GARCH模型是Bollerslev等人于1986年提出的广义自回归条件异方差模型（generalized auto regressive conditional heteroskedasticity，GARCH），主要针对金融时间序列收益率所量体订做的回归模型。除去和普通回归模型的相同之处，GARCH将方差和条件方差区别开来，对条件方差进行自回归建模，适用于波动性的分析和预测。

GARCH模型可表示为GARCH（p，q），模型假定当前时间的条件方差依赖于其滞后值ht－i和残差的滞后值当期的方差决定于三个因素：常数项a0、前一期的残差和前一期的预测方差。

均值方程：

条件方差方程：

式（7）给出的均值方程是一个以Xt以前信息为基础的向前预测方差，称为条件均值方程。在许多文献中以自回归（AR）方程的形式给出。

式（8）给出的方程中：a0为常数项，其余的部分以自回归滑动平均（ARMA）的形式给出。此方程又称条件方差方程，说明时间序列条件方差的变化特征。

式（9）中，N（0，1）为正态分布。

1.4 Matlab在金融时间序列分析实验中的应用

Matlab是科学计算与实验验证的重要工具，在针对时间序列统计特性的分析以及时间序列建模分析的过程中，Matlab提供了大量统计分析函数，如表1所示。

表1 时间序列统计特征计算函数

除统计函数，Matlab也提供了金融分析工具箱，能够进行序列的平稳性检验、GARCH检验、GARCH模型拟合等。

2 具体实验分析与Matlab编码实现

2.1 样本数据的选取

本文选取的股市指数样本数据来源于中国知网国际金融统计数据。数据库从2007年1月1日到2009年12月31日，共3 000个观测值。并且运用Matlab R2007软件进行分析验证。序列的基本信息如图1所示。

图1 深圳股票指数

图1 中，横坐标表示时间，纵坐标从上至下依次为随时间变化的收盘价及成交量（万股）。

首先，针对收盘价进行直接分析可以看出，2007年初的收盘价较为平稳，整体呈现上升趋势，并在2007年10月左右到达峰顶。但在中间一段，也就是2008年金融危机爆发后，波动性明显，所有指数均有很大的下降趋势，而到了2009年，数据有所回复，说明在2008年的金融危机情况下，股市呈下滑趋势。

2.2 数据的统计特征

为了对股票序列进一步分析，以成交量为研究对象，就日收益、日对数收益率、峰度、偏度、方差等进行了计算。

图2和图3分别为深成指数日对数收益率及收益率结果统计图。

图2 深成指数日对数收益率

从图2和图3可以看出：日收益率以及对数收益率都具有波动聚集性，深成指数日对数收益率集中在（－0.05，0.05）之间，在波动较大的几个时段上收益率绝对值达到了0.10，在到达顶峰值后又迅速回落。在样本期间，平均收益率（mediam），即均值为0.002 8，偏度（skewness）为－0.402 9，峰度（kurtosis）为4.202 8，数据分布向左偏移，有一个沉重的尾巴。这说明从整体上看，收益率低于其均值的时候较多，波动性强，头部和中间包含了大量统计信息。

随后对收益率曲线进行自相关与偏相关分析，结果分别如图4和图5所示。

从日收益率的ACF（自相关性）和PACF（偏相关性）看不出日收益率具有明显自相关性。我们可以用Q检验和ARCH检验来检验日收益率序列的自相关性。

2.3 相关性检验

相关性检验的Matlab实现如下所示。

1）Q检验

2）ARCH检验

garchplot（innovations，sigmas，shouyi）

＞＞［H，pValue，Stat，CriticalValue］=…

archtest（seq－mean（seq），［10 1520］′，0.05）；

图3 日收益率统计图及计算结果图

图4 深圳股票自相关指数

图5 深成指数偏相关序列

相关性检验的结果分别如表2和表3所示。

从以上两种检验结果可以发现：在Q检验中，H=0表明，日收益率残差和收益波动不存在自相关性；ARCH检验中，H=1表明，收益率序列具有ARCH效应。均值方程的ht项的系数是0.0012，在5的显著性水平下显著大于0，这表明日收益率与市场风险水平呈弱正相关，验证了高风险对应于高收益的投资组合理论。

表2 Q检验结果

表3 ARCH检验

1.0 0.000 3 41.176 0 24.995 8 1.0 0.003 4 41.331 8 31.410 4

2.4 参数估计

我们利用Matlab金融分析工具箱进行GARCH建模，Matlab实现如下。

1）GARCH拟合

［coeff，errors，LLF，innovations，sigmas，summary］=garchfit（seq）；

2）GARCH参数

garchdisp（coeff，errors）

拟合的参数如表4所示。

条件异方差方程的参数：常数项a0，K值，GARCH项（前一期的方差的预测值ht－1），ARCH项。表4中，第一列为所得值，第二列是标准差，第三列是T检验的数值。

由计算结果用GARCH（1，1）拟合观察值，得出均值方程和条件方差方程。

均值方程：

条件方差方程：

2.5 估计效果分析

GARCH（1，1）模型的β1的系数都比较大且通过了显著性检验，说明股价波动具有“长期记忆性”，即过去价格的波动与其无限长期价格波动的大小都有关系。条件方差方程中，系数a1和β1都显著为正，说明过去的波动对市场未来波动有着正向而减缓的影响，从而使股市波动出现群聚性现象。a1+β1都接近于1，这说明股市波动对外部冲击的反应函数以一个相对较慢的速度递减，股市一旦出现大的波动在短期内很难消除。另外，由于GARCH（1，1）模型中a1+β1小于1，说明收益率条件方差序列是平稳的，模型具有可预测性。

除了参数估计值和标准差，garchfit同时计算了残差（innovations）、条件标准差（conditional standard deviations）。从图6中可以看出，残差出现了波动聚集现象，显示了很强的非平稳性。经过GARCH模型拟合之后，条件标准残差的波动聚集现象已经不明显了。

图6 残差（a）与条件标准差（b）

3 结束语

3.1 本文的主要贡献

本文在对股票指数进行分析时选用了GARCH模型，准确地模拟时间序列变量的波动性的变化。本文所选用的模型在金融工程学的实证研究中应用广泛，尤其是应用在风险价值（value at risk）理论中，使人们能更加准确地把握风险。

GARCH用方差以预测时间序列方差：（1）估计方差，衡量风险；（2）可以计算均值方差中变量的置信区间；（3）对条件异方差正确估计可以使估计参数更准确，特别适用于波动性的分析和预测，这样的分析对投资者的决策能起到非常重要的指导性作用，其意义很多时候超过了对数值本身的分析和预测。

可以预见，未来的研究将会在方法论和工具论两个方向进一步展开，特别是其应用研究还在不断拓展，伴随着市场微观结构理论的成熟，采用ARCH模型来模拟波动性，将会对期货交易制度设计、风险控制制度设计和投资组合风险管理策略研究，提供一个更为广阔的研究空间。

3.2 本文的缺陷及改进的方法

GARCH模型适合在计算量不大时，方便地描述了高阶的ARCH过程，因而具有更大的适用性。但GARCH（1，1）模型在应用于资产定价方面存在以下的不足：

1）GARCH模型不能解释股票收益和收益变化波动之间出现的负相关现象。GARCH（p，q）模型假定条件方差是滞后残差平方的函数，因此，残差的符号不影响波动，即条件方差对正的价格变化和负的价格变化的反应是对称的。然而，在经验研究中发现，当利空消息出现时，即预期股票收益会下降时，波动趋向于增大；当利好消息出现时，即预期股票收益会上升时，波动趋向于减小。GARCH模型不能解释这种非对称现象。

2）GARCH（1，1）模型为了保证非负，假定式（2）中所有系数均大于零。这些约束隐含着的任何滞后项增大都会增加，因而排除了随机波动行为，使得在估计GARCH模型时可能出现震荡现象。

3）此外，针对波动溢出分析，原始GARCH模型仅能支持单一金融市场，难以对不同市场之间的相互影响进行分析。

3.3 改进的方法

如果要对波动溢出做进一步分析，可以考虑如下方法：

1）主成分分析与独立成分分析。通过多个金融市场的收益率波动数据构成协方差矩阵并计算主成分和独立成分，并与GARCH模型相结合的方法来进行分析。

2）建立多个金融市场的时间序列矩阵，引入多变量GARCH模型或矢量GARCH模型（bekkmgarch），才能达到理想的分析结果。

［1］Fama E F.The behavior of stock－market prices［J］.The Journal of Business，1965，38（1）：34－105.

［2］文雪梅，柏满迎.股票收益率预测模型的比较［J］.现代商业，2009（11）：26.

［3］赵耀军.时间序列分析［J］.山西冶金，2012（6）：19.

［4］张树京，齐立心.时间序列分析简明教程［M］.北京：清华大学出版社，2003.

［5］张善文，雷英杰，冯有前.Matlab在时间序列分析中的应用［M］.西安：西安电子科技大学出版社，2007.

［6］林建华，王福昌，冯敬海.股价波动的指数O2U过程模型［J］.经济数学，2000，17（4）：29－32.

Volatility M odelling of Chinese Stock M arket Based on M atlab

CONG Chao，XU Deling，PANG Shida，SUN Kaixuan
（School of Electronic Information and Automation，Chongqing University of Technology，Chongqing 400054，China）

On the background of a global financial turmoil，mathematical，statistical and economic analysiswas applied in the experiment of analyzing the volatility feature of Shanghaiand Shenzhen stock indexes from 2007 to2009.Then，a Matlab based financial toolbox and GARCH（generalized auto regressive conditional heteroskedasticity）modelingmethodswere used in the experiment.The result showed an obvious heteroscedasticity feature in return series and a very good fitting with GARCH model.

stock market；time series analysis；generalized auto regressive conditional heteroskedasticity；Matlab program

TP311；F832.5

A

10.3969/j.issn.1672－4550.2014.05.022

2013－06－06；修改日期：2014－07－12

丛 超（1984－），男，硕士，助理实验师，研究方向：图像处理、软件开发、高性能并行计算。