质量不确定的回收品采购量及再制造排序策略

杨爱峰， 季园园， 胡小建， 杨海洪

（合肥工业大学 管理学院，安徽 合肥 230009）

0 引言

近年来，经济快速发展使人们生活发生了翻天覆地的变化，但随之而来的是大量废旧品的产生，如何处理这些废旧品引起了社会各界的广泛关注。当前基于全生命周期理念的再制造，已经成为处理废旧品的一种有效途径［1－3］。

再制造是一种对废旧产品实施高技术修复和改造的产业，它针对的是损坏或行将报废的零部件，在性能失效分析、寿命评估等分析的基础上，进行再制造工程设计。再制造能延长产品的使用寿命，提高产品技术性能和附加值，最终以最低成本、最少能源及资源消耗完成产品的全生命周期。例如，卡特彼勒作为世界上最大的重型机械生产商，目前在全球包括中国在内的8个国家拥有19家再制造工厂，再制造废旧单体发动机220万件以上，质量占85%的零部件可被再制造或再利用，节约金属超过6×104t，再制造产值在2011年已超过20亿美元。

文献［4－7］研究了制造与再制造混合库存模型、再制造闭环供应链和再制造产品定价等。再制造活动中，非常现实的问题是回收品的质量具有高度不确定性，于是再制造的一个关键环节是需要决策回收品的采购批量以及检测回收品是否适合再制造。

文献［8］建立了质量不确定情况下对翻新产品进行处理的模型，以仿真美国陆军仓库的逆向物流网络；文献［9］研究了提高回收废旧品质量的激励措施，当回收品质量越高时，需要的再制造成本越低，可再制造的比例也就越高；文献［10］研究了回收质量的不确定性，并将建立的逆向物流网络中的再制造成本设定成一个常数；文献［11－12］在建模运算时，也认为再制造成本是固定的；文献［13］讨论了不同回收过程中应选择的不同策略，模型中认为回收产品质量是满足均匀分布的，且产品的再制造成本是固定的；文献［14］在模型中，将再制造成本表示为固定成本和可变成本之和的形式，并给出假设可变成本是线性模型和非线性模型2种不同情况下的解法；文献［15］建立了质量不确定情况下的闭环供应链选择模型，模型中的再制造成本用维修率、拆解率及分解率表示。

上述文献在考虑回收产品质量不确定性时，再制造成本是固定的或是固定成本和可变成本之和。

本文不同之处在于将再制造成本看成是依赖于检测结果的一个函数，即成本是不固定的。在建立模型时，假设回收品的质量是服从某种分布的随机变量，检测排序后的废旧品只有再制造或处理2种结果，且认为废旧品经过检测中心排序后，其再制造所需成本就成为已知数。

1 模型假设

本文研究的再制造系统包含了回收中心、排序中心、再制造中心及销售中心，系统流程如图1所示。

再制造企业首先将采购的废旧品运往回收中心，然后根据回收品质量及再制造生产计划进入排序中心检测排序，其结果是部分回收品直接处理，其余的进行再制造，再制造活动在再制造中心进行，再制造品进入销售中心等待销售。

若再制造品数量少于需求，则产生缺货成本；相反，将对其进行处理，即在二级市场销售或当成废物报废。

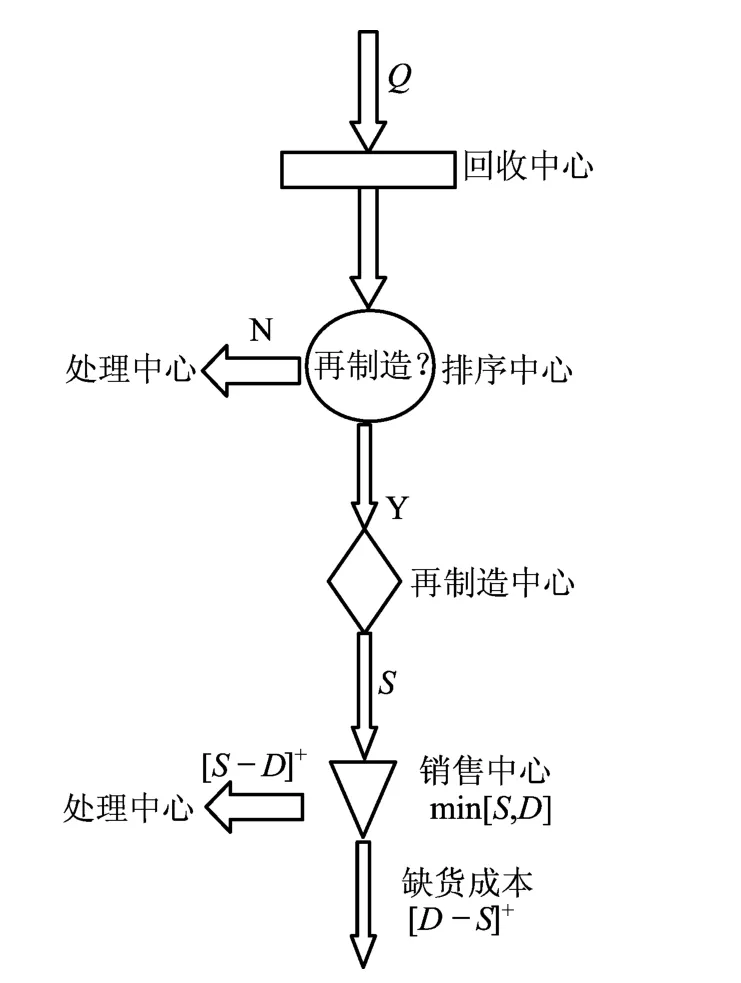
图1 再制造系统流程图

图1中，Q为回收品的采购批量（决策变量）；S为回收品再制造批量（决策变量）；D为市场需求量。

定义符号如下：α为回收品进行再制造的比例，α＝S／Q；t为经检测产品用于再制造的最大成本；Ct为单位运输成本；Ca为单位采购成本；Cs为单位排序检测成本；Cr为再制造的平均单位成本；Cp为单位缺货成本；Cd1为未进行再制造回收品的单位处理成本；Cd2为未售出的再制造品单位处理成本；v为再制造品的单位售价（＞Cr）；G（·）为回收品质量分布函数；g（·）为相应的概率密度函数；F（·）为需求的分布函数，f（·）为相应的概率密度函数。

本文假设检测排序环节结束后，每个回收品的再制造成本变为确定数。排序策略由再制造的最大成本t值描述，当回收品耗费的再制造成本大于t时，回收品将被处理，相反，则进行再制造。再制造的平均单位成本Cr依赖于排序检测结果，即

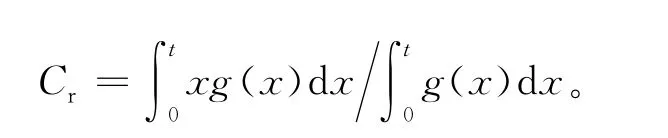
另外，Cd1和Cd2值正负均可。如果处理的方式是报废，则Cd1和Cd2值为正；如果是在二级市场销售，则Cd1和Cd2值为负，这时可以假设－v＜Cd2≤Cd1，并且Cr≥Cd1－Cd2，因为Cd1－Cd2表示的是因为再制造而产生的产品增值，如果Cr＜Cd1－Cd2，说明即使再制造品没有被销售的可能，也要将所有废旧品进行再制造，与现实不符。

2 模型建立与求解

本文以排序中心为交界节点，将整个再制造系统流程分为2个阶段。

第1阶段是再制造企业将采购的废旧品运往回收中心，然后进入排序中心检测排序，需要决策废旧品的采购批量及排序策略；第2阶段是将符合要求的废旧品运往再制造中心进行再制造，再制造成品在销售中心等待销售，需要决策的是再制造批量。

整个建模求解思路是从第2阶段入手，通过计算系统的平均利润，决策出最优的再制造批量S＊，再将S＊代入到第1阶段进行考虑，决策出回收品的最佳收购批量Q＊和排序策略t＊。

第2阶段再制造系统的利润为：

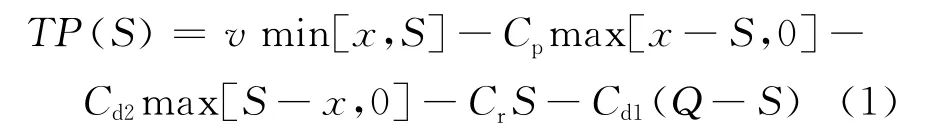
其中，第1项为再制造品的销售收入；第2项为再制造品的缺货成本；第3项为未销售的再制品处理成本；第4项为再制造成本；第5项为未进行再制造的废旧品处理成本。

于是平均利润函数为：

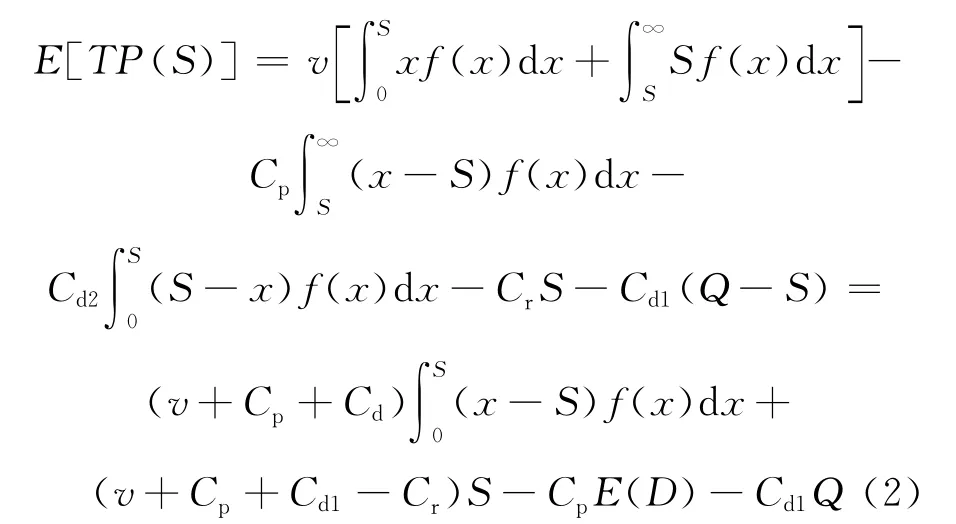
对E［TP（S）］关于S求一阶偏导，即

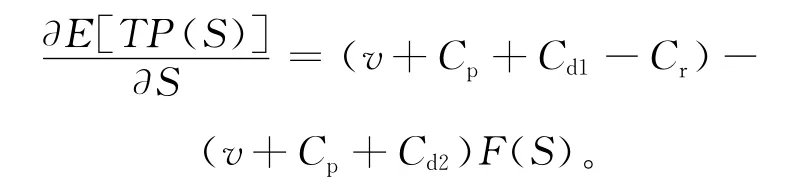
令∂E［TP（S）］／∂S＝0，可得：

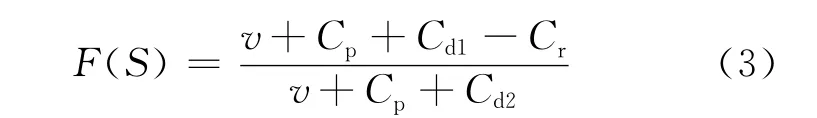
前面假设中提到v＞Cr，Cr≥Cd1－Cd2，显然可得（3）式的分子、分母都大于0，且分母大于分子，所以此解符合实际情况。再求出（2）式关于S的二阶偏导，即

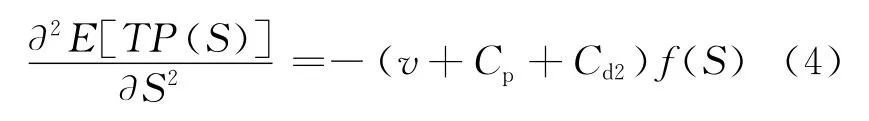
显然（4）式小于0，所以存在最优解S＊，使其平均利润函数取最大，即

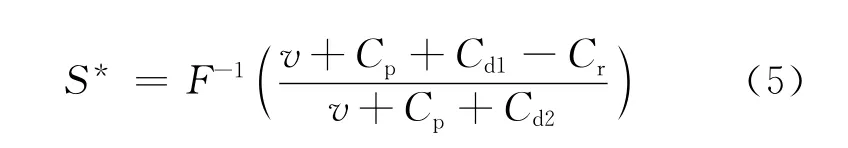
由（5）式可知，S＊的取值与再制造成本Cr有关，随着Cr的增大而减少。又因为回收品质量的不确定性，Cr值依赖于检测排序的结果，并不固定，故再从第1阶段开始考虑。

由假设可知，对于给定的G（·），α和t可以表示为：

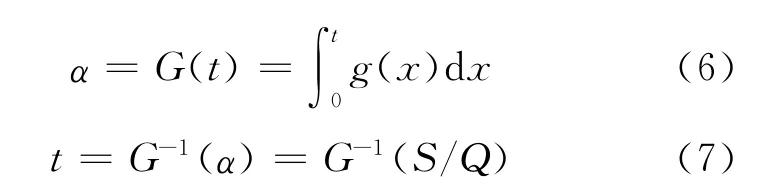
（7）式即是再制造系统最佳排序策略的数学表达式。再制造成本为：

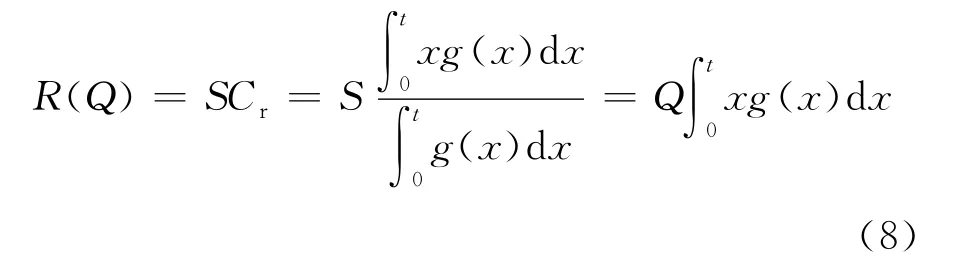
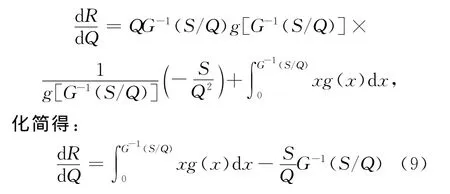
将（9）式中S／Q提出，可得：

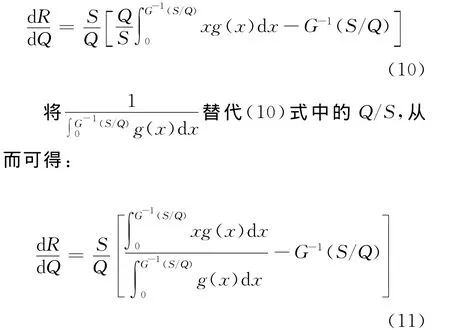
对Q求二阶导数，将（11）式改写为：

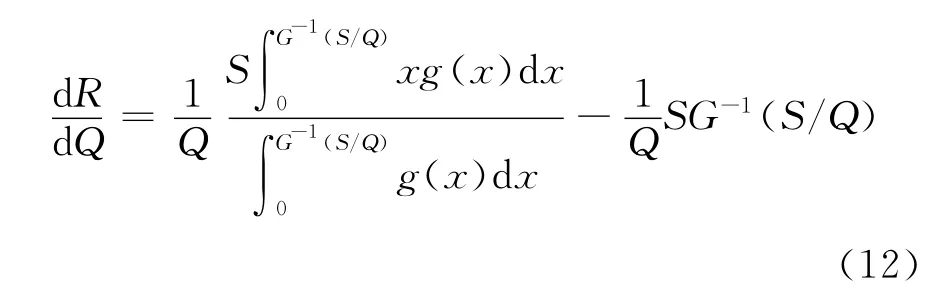
将（12）式中第1项对Q再次求导，并将（8）式带入，可得：

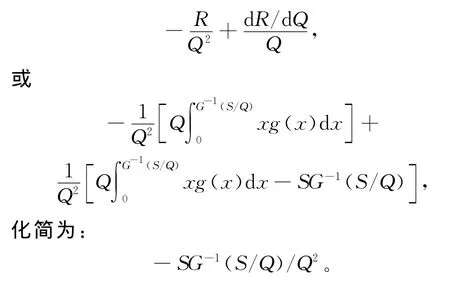
（12）式的第2项对Q再次求导，可得：

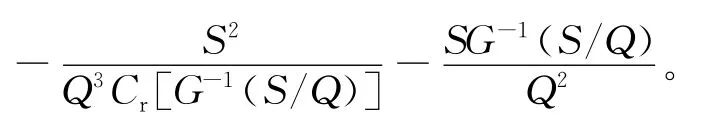
因此，可得：

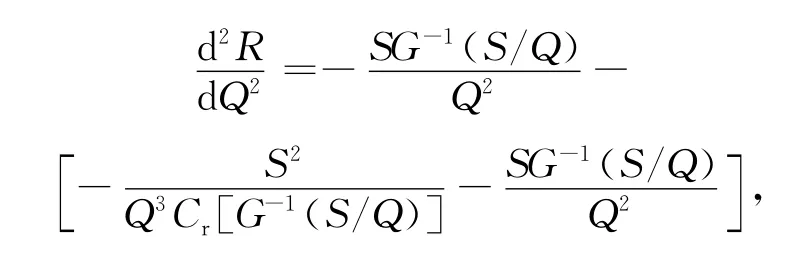
化简得：

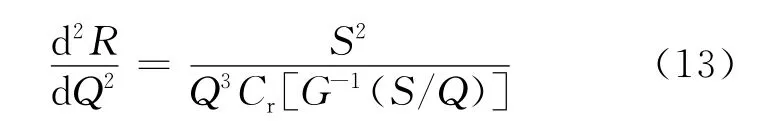
很显然（13）式大于0，于是可知平均再制造成本R（Q）是关于收购批量Q的凸函数，即可求出使R（Q）达到最小的最优值Q＊。

基于此，对模型的第1阶段所需成本进行研究，此时关于α的成本为：

由（15）式可以看出，平均总成本与再制造批量S及废旧品采购批量Q值无关。由此可以把假设中v＞Cr扩展成v＞TU，这样更符合经济学规律。因此，可以把模型的求解归纳为以下3个步骤：

（1）根据回收品质量函数得到α，将其代入（15）式，求出TU＊。计算结果见表1所列。

（2）利用α算出C＊r，并带入（5）式，求出S＊。

（3）决策出最优的收购批量Q＊＝S＊／α。

3 算 例

令Cα＝2，Ct＝1，Cs＝1，Cp＝4，v＝20，Cd1＝－2，Cd2＝－8，G（·）符合伽玛分布，F（·）服从［150，2 000］上的均匀分布。为方便表示，令Cz＝Cα＋Ct＋Cs。计算结果见表1所列。

由表1可知，随着再制造比例α的不断增加，用于再制造的最大成本t随之增加，平均再制造成本Cr不断增加，同时TU也逐步增加，最终导致再制造产品数量及收购批量减少。

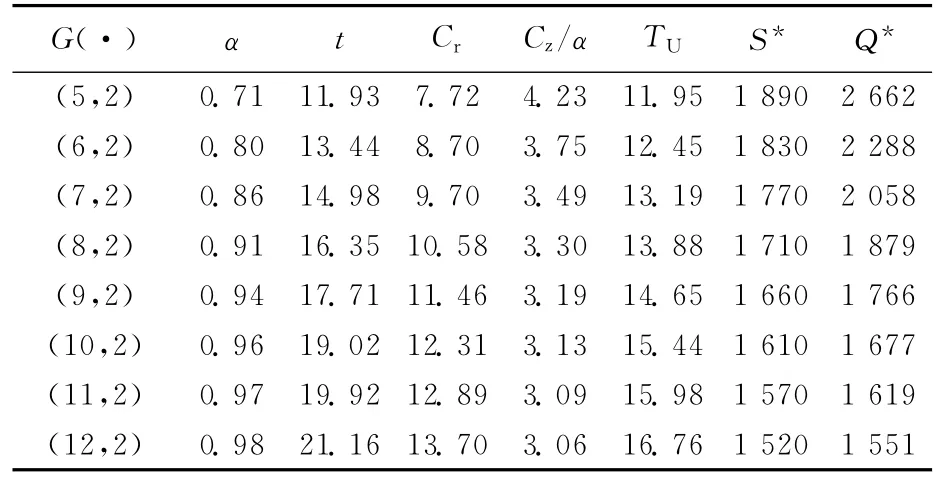
表1 再制造比例的变化对单位再制造成本的影响

从实际意义上看，当增加回收品的收购数量时，可供排序中心筛选的废旧品也变多，其中质量较高的回收品将会以更大的数量优先进入再制造流程，最终使再制造平均成本降低。

4 结束语

本文研究了回收质量不确定情况下的采购数量及排序策略，给出合理的假设，并决策出单周期产品的最优采购和排序方案，结果发现最佳排序策略与再制造数量及采购数量无关，平均再制造成本的变化也与采购数量无关。本文中再制造比例根据废旧品的质量分布直接确定，而在现实中，这个数字要满足企业以及社会当前的再制造水平和很多指定条件，这是今后需要解决的问题。此外，对于如何解决多阶段产品的再制造问题也需要进一步探索。

［1］Seitz M A，Peattie K.Meeting the closed－loop challenge：the case of remanufacturing［J］.California Management Review，2004，46（2）：74－89.

［2］Thierry M，Salomon M，Van Nunen J，et al.Strategic issues in product recovery management［J］.California Management Review，1995，37（2）：114－135.

［3］Toktay L B，Wein L M，Zenios S A.Inventory management of remanufacturable products［J］.Management Science，2000，46（11）：1412－1426.

［4］杨爱峰，王 晓.基于回收价格的再制造系统策略研究［J］.合肥工业大学学报：自然科学版，2011，34（4）：593－597，608.

［5］Pokharel S，Muthab A.Perspectives in reverse logistics：a review resources［J］.Conservation and Recycling，2009，53：175－182.

［6］Gupta S，Palsule－Desai O D.Sustainable supply chain management：review and research opportunities［J］.IIMB Management Review，2011，23：234－245.

［7］Gilvan C S.Closed－loop supply chains：a critical review and future research［J］.Decision Sciences，2013，44（1）：7－38.

［8］Humphrey A S，Taylor G D，Landers T L.Stock level determination and sensitivity analysis in repair／rework operations［J］.International Journal of Operations ＆ Production Management，1998，18（6）：612－630.

［9］Klausner M，Hendrickson C T.Reverse－logistics strategy for product take－back［J］.Interfaces，2000，30 （3）：156－165.

［10］Krikke H R，Van Harten A，Schuur P C.Business case oce：reverse logistic network redesign for copiers［J］.OR Spektrum，1999，21：381－409.

［11］Jayaraman V D，Guide R，Srivastava R.A closed－loop logistics model for remanufacturing［J］.Journal of the Operational Research Society，1999，50：497－508.

［12］Majumder P，Groenvelt H.Competition in remanufacturing［J］.Production and Operations Management，2001，10（2）：125－141.

［13］Savaskan R C，Bhattacharya S，Van Wassenhove L N. Closed－loop supply chain models with product remanufacturing［J］.Management Science，2004，50（2）：239－252.［14］Galbreth M R，Blackburn J D.Optimal acquisition quantities in remanufacturing with condition uncertainty［J］.Production and Operations Management Society，2010，19（1）：61－69.

［15］高 阳，李 辉.基于回收质量不确定的闭环供应链回收渠道选择［J］.工业技术经济，2011（11）：5－11.