基于热点应力法的正交异性钢箱梁疲劳评估

王 超， 朱宏平， 钟继卫

（1.华中科技大学 土木工程博士后流动站，湖北 武汉 430074；2.中铁大桥局集团 武汉桥梁科学研究院有限公司，湖北 武汉 430034）

在长期交通荷载作用下，由于加载和卸载产生的交互应力可能导致钢箱梁产生累积损伤，严重时会发生疲劳破坏，危及桥梁的安全运营。传统的疲劳评估大多是基于名义应力法［1－2］。首先统计分析结构危险焊缝处的应力谱，再基于线性疲劳累积损伤准则和疲劳强度曲线（S－N曲线）对结构进行疲劳寿命评估。实际结构是非常复杂的，很难精确定义构件焊缝连接部位的名义应力，当前有限元分析法广泛应用于结构分析，但很难直接从计算结果推导出结构的名义应力。另外，一些实际焊接连接类型十分复杂，很难分清细节连接类型而选取相应的疲劳强度曲线。为此近年来许多学者提出采用热点应力法对结构进行疲劳评估，并在相关的理论研究、实验研究和工程实际应用上取得了一些进展［3－7］。

进行疲劳评估的关键问题之一是获得结构应力谱，传统模拟法依靠交通调查和统计分析建立疲劳车并在桥上加载，通过有限元计算得到构件的应力时程，从而实现应力谱的计算。该方法现场交通调查工作量很大，并且有限元计算各种假定误差、桥梁振动、车辆偏载的影响需要修正，很难准确再现桥梁实际的工作状态。随着桥梁健康监测技术的发展，可在桥上布设应力测点，直接测定结构疲劳关键部位的应力时程，由此得到的应力谱更接近实际，并且减少了许多调查工作。

本文基于热点应力法对正交异性桥面板钢箱梁进行评估，通过有限元模拟分析疲劳危险连接部位的应力集中因子，根据健康监测系统实测的应力数据计算结构的热点应力时程，并统计结构的标准日应力谱，基于热点应力强度曲线（Shot－N曲线）对结构进行疲劳评估。将提出的方法应用于实际钢箱梁桥的疲劳评估。

1 热点应力法

热点应力是指最可能发生疲劳裂纹的起始点处的应力，也称为几何应力，因为它与结构构件及整体的几何尺寸和受载条件有关。焊趾部位的局部应力增大可分为：① 构件及接头的整体几何不连续导致的几何应力集中；② 焊趾形状、裂缝及切口等局部缺口效应引起的缺口应力集中。热点应力法仅考虑几何应力集中，通常认为热点应力主要由薄膜应力和弯曲应力组成，是构件表面热点处薄膜应力与弯曲应力之和的最大值。焊趾局部缺口效应通过在热点应力强度曲线（Shot－N曲线）中予以考虑。

热点应力法的一个关键问题是合理确定结构的热点应力，通常可以通过对结构有限元分析的结果进行后处理来得到。文献［8－9］提出了不同的计算方法，最流行的方法是表面外推法，该方法通过焊趾附近的两点或三点应力进行线性或二次差值来推算热点应力。两点线性插值外推法的计算模式如图1所示。

选择合适的外推方法及外推点是关键的问题，本文采用挪威船级社（DNV）推荐的两点线性插值表面外推算法，插值点应力分别取距离焊趾0.5t和1.5t点的应力，t为板厚。

图1 两点线性插值表面外推法示意图

热点应力法考虑了结构的几何不连续导致的应力集中，理论上完全可以使用一条通用的热点应力强度曲线来考虑各种不同接头焊缝类别的疲劳强度，避免了名义应力法中复杂构件连接细节分类的难题。Shot－N曲线可表达为：

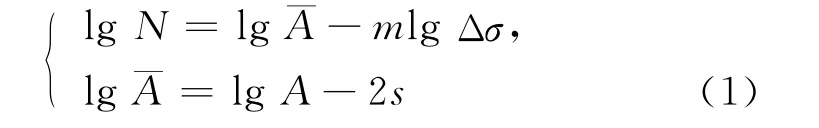
其中，Δσ为应力幅；N为应力循环数；m为与曲线斜率相关的参数；¯A为截距参数；A为与存活率为50%的均值Shot－N曲线有关的参数；s为lgN的标准差。

本文采用DNV推荐的一条通用的Shot－N曲线进行疲劳评估，该曲线如图2所示。该曲线规定对应的N＝1×107次和N＝1×108次时的应力幅分别为常幅疲劳极限ΔσL＝52.63MPa和疲劳截止限Δσout＝33.20MPa。

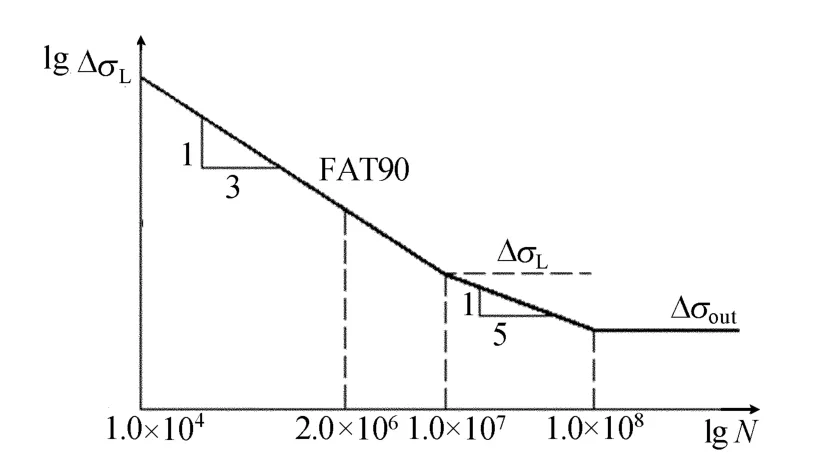
图2 DNV推荐的Shot－N 曲线

2 基于实测应力的疲劳评估

2.1 标准日应力谱（SDSS）

将健康监测系统实测的应力进行预处理后，采用雨流计数法将其转化为应力循环，按应力幅水平分段统计各段循环次数，可得到应力谱。理论上所有运营阶段的应力时程统计得到的应力谱最能反映结构真实的疲劳响应，但海量数据的处理费时，且不必要。实际上在一段时间内，交通荷载变化较小，可选取一段有代表性的数据进行统计分析，如2周的数据，它包含了从周一到周日2个周期的交通流状况，因此，本文采用的统计应力谱如下：

（1）分别对每天的数据进行雨流统计得到每天的应力谱，定义为日应力谱（DSS）。

（2）对当天和其之前多天的日应力谱进行统计平均得到新的应力谱，定义为标准日应力谱（SDSS）。

2.2 基于Shot－N曲线的疲劳评估

统计出SDSS后，可以基于线性累积损伤准则和Shot－N曲线对结构进行疲劳评估。假定在应力幅为Δσi，对应循环次数计为ni的等幅荷载作用下，结构的累积损伤度为：

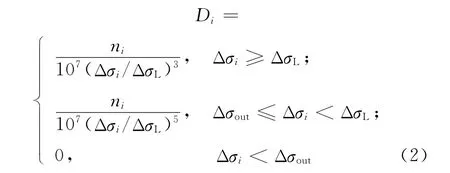
在SDSS所有应力循环 Δσi、ni（i＝1，2，3，…）作用下，结构每天的累积损伤度为：

结构的预期寿命为：

假如结构的设计寿命为Ns，则服役期截止后，结构的累积损伤度为：

3 工程应用

将提出的方法应用于军山大桥疲劳评估。该桥是一个大跨度正交异性桥面板钢箱梁斜拉桥，主桥跨径布置为48m＋204m＋460m＋204m＋48m。为监测大桥安全运营，大桥安装了健康监测系统，在主跨1／4断面钢箱梁内布设了大量的应变传感器。通过对钢箱梁疲劳危险调研和分析，本文主要对钢箱梁顶板与U肋纵桥向连接焊缝和U肋下缘与横隔板连接焊缝进行疲劳评估，如图3所示。每类连接位置选取了6个测点，测点布置如图4所示，测点按从左到右顺序编号为2－1，2－2，…，2－6。

健康监测实测应力是结构的名义应力，为了获得结构的热点应力，需要计算结构焊趾位置的应力集中因子（SCF），定义为热点应力与名义应力的比值，可通过有限元模拟计算获得。本文采用大型通用有限元分析软件ANSYS建立钢箱梁节段模型，采用具有中节点的壳单元建模，在2类焊接连接处进行了精细网格划分以获取精确的局部应力集中结果。局部有限元模型如图5所示。通过求解有限元模型，计算出2类焊接连接部位的应力集中因子分别为1.55和1.49。

图3 测点位置示意图

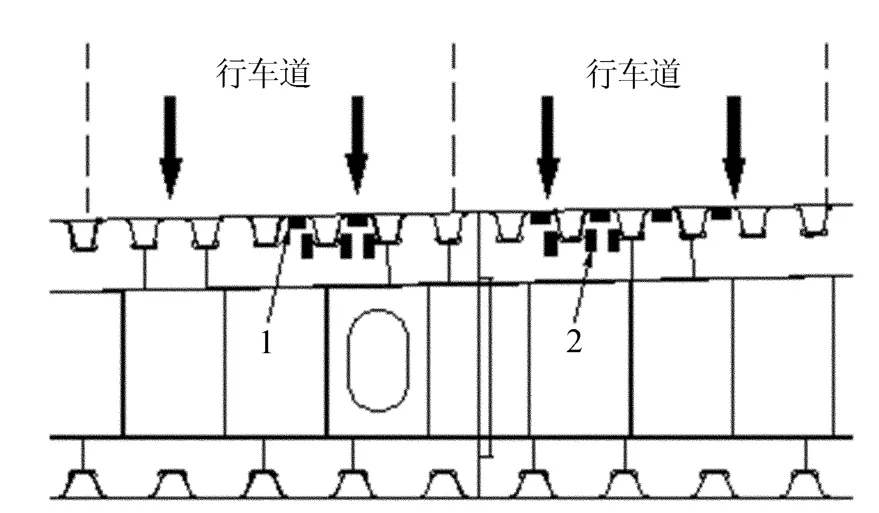
图4 测点布置图

图5 钢箱梁局部有限元模型

本文提取了健康监测系统16d的应力数据进行分析。通过所得的应力集中因子计算焊趾的热点应力时程，随后进行标准日应力谱统计。为比较日应力谱和标准日应力谱的不同，分别统计计算从2011年11月9日—18日共10d的日应力谱和标准日应力谱（每天的标准日应力谱采用当天及之前1周的数据来计算），并对钢箱梁进行疲劳评估。采用不同应力谱对测点2－4进行疲劳评估的结果如图6所示。

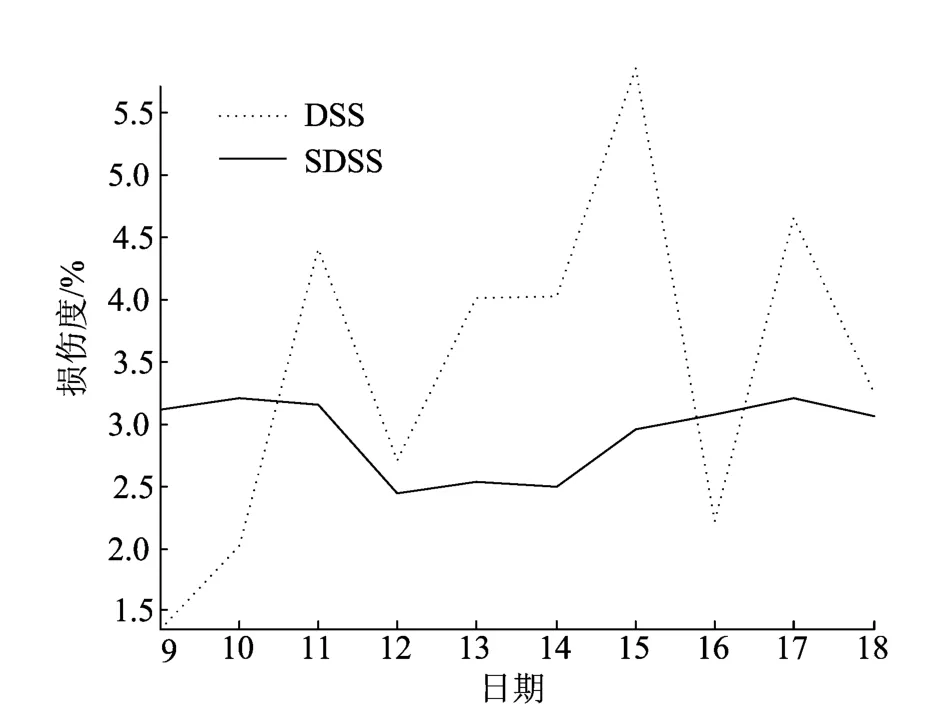
图6 测点2－4日应力谱和标准日应力谱疲劳评估结果

由图6可见，采用日应力谱的评估结果受每天交通量的影响较大，标准日应力谱的评估结果波动明显减小。显然，如果采用更多天的数据进行统计获得标准日应力谱，评估结果更稳定。

基于线性累积损伤准则和Shot－N曲线对2类焊缝连接进行疲劳评估，结果见表1所列。

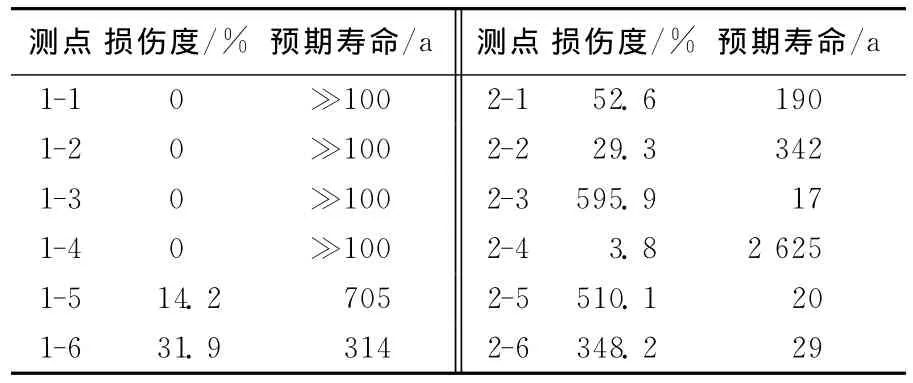
表1 疲劳评估结果

由表1可看出，在当前交通状况下，军山大桥钢箱梁顶板与U肋纵向桥梁焊缝连接在设计使用期结束时结构的累积损伤小于100%，结构不会发生疲劳破坏。而U肋下缘与横隔板焊缝连接中除测点2－1和2－4外累积损伤均超过100%，因此在钢箱梁U肋下缘与横隔板连接部位将会发生疲劳破坏。主要是由于该部位U肋的挠曲变形受到横隔板约束而产生很大的次弯曲应力。同时，横隔板的竖向挠曲变形在该部位产生较大的面内弯曲应力和剪应力，实桥在巡检过程中发现可见水平疲劳裂纹。因此，该部位是钢箱梁的疲劳薄弱部位，应重点监测，加强维护。

4 结论

本文基于热点应力法对正交异性桥面板钢箱梁进行疲劳评估，通过有限元模拟分析计算结构的应力集中因子，并通过健康监测系统实测应力来计算焊趾的热点应力，提出了标准日应力谱统计的方法，将该方法用于军山大桥钢箱梁疲劳评估。研究结果表明：

（1）钢箱梁疲劳评估结构与桥梁实际检测结果一致，表明基于热点应力法的钢箱梁疲劳评估方法是准确有效的。考虑到计算时间和精度要求，当采用健康监测实测应力进行标准日应力谱统计时，2周的数据量具有一定的代表性。

（2）U肋下缘与横隔板焊接连接部位是正交异性桥面板钢箱梁的疲劳薄弱部位，该部位应力集中明显，在当前交通荷载作用下将产生疲劳破坏，应重点监测，加强维护。

［1］Li Z X，Chant H T，Ko J M.Fatigue analysis and life prediction of bridges with health monitoring data，partⅠ：methodology and strategy［J］.International Journal of Fatigue，2001，23（1）：45－53.

［2］Chan T T，Li Z X，Ko J M.Fatigue analysis and life prediction of bridges with health monitoring data，part II：applications［J］.International Journal of Fatigue，2000，23（1）：55－63.

［3］周张义，李 芾，黄运华.基于热点应力的焊缝疲劳强度评定研究［J］.内燃机车，2008（7）：1－5.

［4］陈有芳，金秋东，张少雄.船舶热点疲劳强度研究［J］.船海工程，2010（2）：5－7.

［5］王斌杰，李 强，刘志明，等.轨道车辆焊接接头热点应力计算研究［J］.铁道学报，2011，33（11）：28－33.

［6］王国波，谢伟平，于艳丽.高速列车荷载作用下铸钢焊接节点的疲劳分析［J］.振动与冲击，2011（9）：55－58.

［7］Lotsberg I.Fatigue design of plated structures using finite element analysis ［J］.Ships Offshore Structures，2006，1（1）：45－54.

［8］Dong P.A structural stress definition and numerical implementation for fatigue analysis of welded joints［J］.International Journal of Fatigue，2001，23（10）：865－876.

［9］Xiao Z G，Yamada K.A method of determining geometric stress for fatigue strength evaluation of steel welded joints［J］.International Journal of Fatigue，2004，26（12）：1277－1293.