基于分布估计算法的无线传感器网络覆盖问题优化

李慧凯,王筱萍,高慧敏

(嘉兴学院：a.机电工程学院;b.商学院,浙江嘉兴314001)

0 引言

无线传感网络 (Wireless Sensor Net works,WSN,也称传感器网络)由大量具有感知能力、计算能力和通信能力的微型传感器以自组织方式构成,在新一代网络中具有关键性角色。但由于应用规模大,能量、计算能力和通信能力受限等特点,在监测区域内要对传感器节点进行大规模、高密度冗余部署,这就造成部署代价与部署质量、节点能量受限以及网络生存时间之间的矛盾,而覆盖控制通过对节点感知能力的建模,使无线传感器网络的空间资源得到优化分配,进而更好地完成环境感知、信息获取和有效传输的任务.

任丰原等详细阐述了包括低功耗路由技术和介质访问控制方法在内等热点研究问题.[1]班庆奇等给出了传感器节点的感知模型,从不同角度对覆盖问题进行分类,阐述覆盖控制算法的评价指标,介绍覆盖问题和连通问题的典型算法,并对覆盖和连通问题的研究方向进行了展望.[2]王伟等分析无线传感器网络的网络特征以及影响网络覆盖的重要因素,总结和评估近年来提出的覆盖机制,同时对该领域尚存问题以及发展趋势进行了讨论.[3]吕广辉等对遗传算法中的适应度函数公式做了改进,将多重覆盖率和覆盖率的组合作为适应度函数.根据遗传算法的相关内容和流程图,利用遗传算法对覆盖策略做仿真模拟,证明了所选用方法的正确和优越性.[4]张西红等研究了在满足覆盖性和连通性要求的基础上,选择最少数量的工作节点以及计算同时满足覆盖要求和连通性要求的问题.[5]

分布估计算法 (EDAs)是一类基于概率模型的进化算法,与传统的进化算法不同,它不使用交叉和变异算子,而是根据当前种群的概率分布来产生下一代的种群,即先从当前种群中按照一定的选择方式选出一部分适应度较好的个体,根据他们建立概率分布模型,再利用所建分布模型产生新的个体,如此迭代直到满足终止条件.基于概率的分布估计算法是一种来自于统计学的进化算法,比传统的进化算法有更强的理论基础以及较强的收敛性,操作性也更强.[6-7]周树德等根据概率模型的复杂性,按照变量无关、双变量相关、多变量相关等三类分别介绍了相应的分布估计算法.[8]

算法实施流程如图1所示.

本文提出一种基于加权分布估计算法的覆盖优化策略,它能快速实现最优节点集的选取,从而降低能耗、延长网络生存时间.

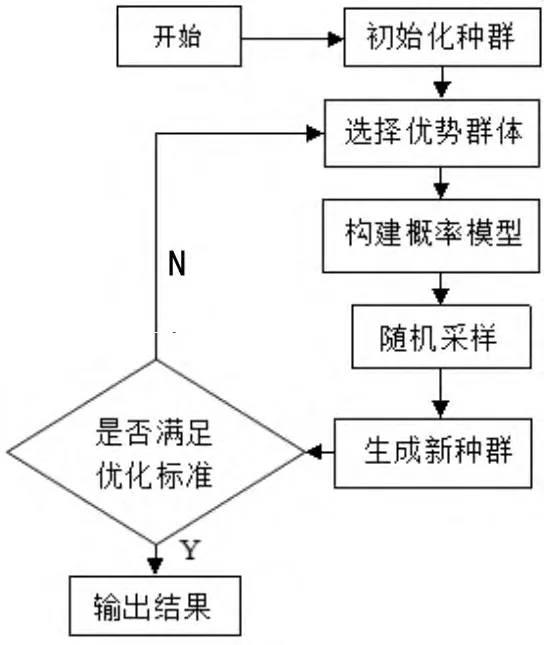
图1 分布估计算法流程图

1 覆盖问题建模

1.1 相关假设

1.2 覆盖问题模型

无线传感器网络优化覆盖问题是一个典型的目标优化问题.传感器网络有效覆盖率 (Cov Area)、工作节点数目 (nu m_wor ksen)是衡量工作节点集选取的重要指标.为计算Cov Area,将目标区域A划分为m×n个网格,以网格中心被覆盖的程度代表网格被覆盖的程度,Δs表示每个网格的面积,As表示目标区域A的总面积,则有：

由式 (1)可知网格G(xl,yw)被节点ci覆盖的概率为：

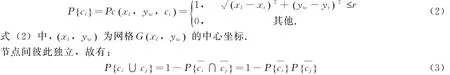
网格被节点集覆盖的概率为：

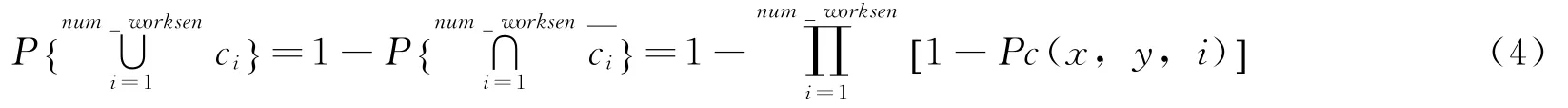
则工作点集C的区域覆盖率Cov Area(C)为节点集覆盖面积与目标区域总面积的比值,即：

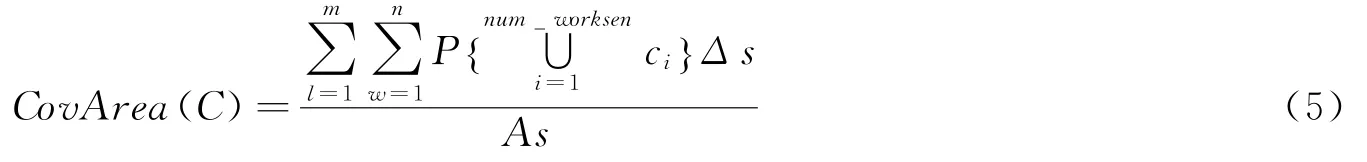
另外,若工作节点的数量为num_wor ksen,则节点利用率Sen Rat(C)为：

2 基于加权分布估计算法的覆盖优化策略

2.1 编码方式

在分布估计算法中,选择合适的编码方式并将最优化问题的解空间和编码空间相互映射是一个关键问题.在无线传感器网络中,传感器节点是随机分布的,由此在分布估计算法中一个个体应代表在一个固定位置的传感器节点,同时编码方式需要突出每个节点的工作状态.这里采用0～1编码的方式,染色体用一串二进制数表示,其中每一位代表一个节点,节点的位序表示传感器的序号,用1代表节点为工作状态,用0代表节点为静默状态.即覆盖问题的解由位串a=(a1,a2,…,aN)表示,其中：

2.2 基于加权的适应度函数设计

工作节点集的网络覆盖率子目标函数为：

若作用点高度保持一致，对同一种品种而言，不同的作用点高度(由于实验系统测量范围的限制，一般作用点高度在第2节间之上)，测量T以及a值，观测其曲线变化，亦可定量地了解同一单株小麦茎秆不同节间的机械强度变化，回弹力T值越大，茎节间茎秆机械强度越强。该评价指标也适用于其他茎秆作物，如玉米、水稻和谷物等。

节点利用率子目标函数为：

本文中将覆盖率函数f1(x)与节点利用率函数f2(x)作为子目标函数,总体目标函数是这两个子目标函数的变换加权和.总体目标函数可定义为：

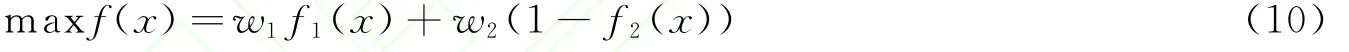
其中w1和w2为子目标函数对应的权值,其值取决于设计者对该传感器网络指标的综合要求.权值满足条件ω1+w2=1,则总体目标函数值介于0～1之间.通过式 (10),可综合评估各种节点部署方案的优劣.

3 实验及分析

本文采用Matlab 7.0软件进行仿真.软件运行环境Windows 7系统,CPU主频2.1 GHz.实验一为半定点半随机区域覆盖,实验二为随机节点区域覆盖,实验三为随机点覆盖.每个实验均独立运行50次,取其平均值.

设定目标区域大小为100×100,传感器节点数目N为50,感知半径R为20,覆盖率子目标函数权重w1为0.7,节点利用率子目标函数权重w2为0.3,群体规模为10,进化代数为30.

3.1 实验一

50个传感器节点由14个确定位置的传感器节点和36个位置随机产生.14个确定位置的最优覆盖传感器节点坐标由文献 [3]和文献 [4]提供的 “六边形法则”确定.算法运行15代,观察不同代数的节点分布.

将覆盖率子目标函数权重w1分别更改为0.5、0.3,相应的权重w2变为0.5、0.7,分别进行实验.统计40次运行的结果,权重不同时对适应度、覆盖率及节点利用率的影响如图2～4所示.

从3个图不难看出,覆盖率函数的权重变大,最优节点集的覆盖率变大,相应的节点利用率的权重变低,因而造成节点利用率增大,使传感器节点数增加.

因此,可以根据实际需求,通过调节权重,使最优节点集侧重于工作节点数目减少抑或覆盖面积增加.

3.2 实验二

将节点部署方式改为全随机部署,节点感知半径分别设置为15、20、25进行实验.同样统计50次实验结果,感知半径时对适应度、覆盖率及节点利用率的影响如图5～7所示.

由实验二的结果可知,对于相同数目的传感器节点,在同样做到冗余覆盖的情况下,节点感知半径更大的传感器网络,由本文策略进化出的最优节点集能够实现更好的网络覆盖质量.

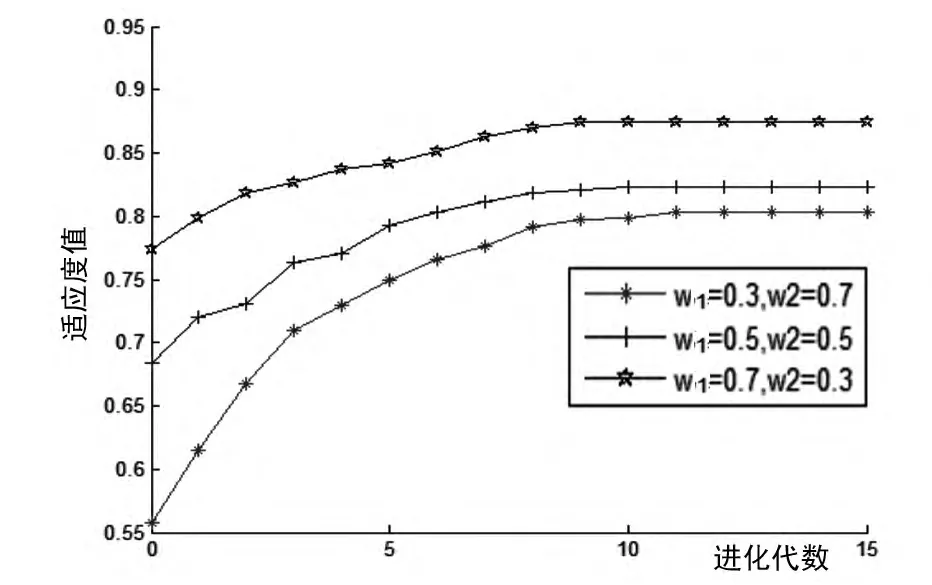
图2 权重对适应度的影响图

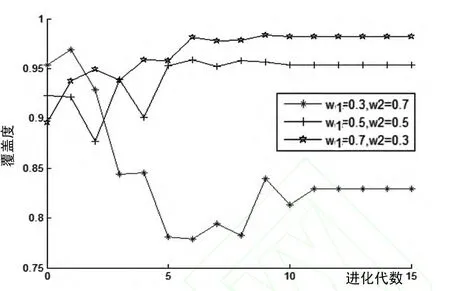
图3 权重对覆盖率的影响图

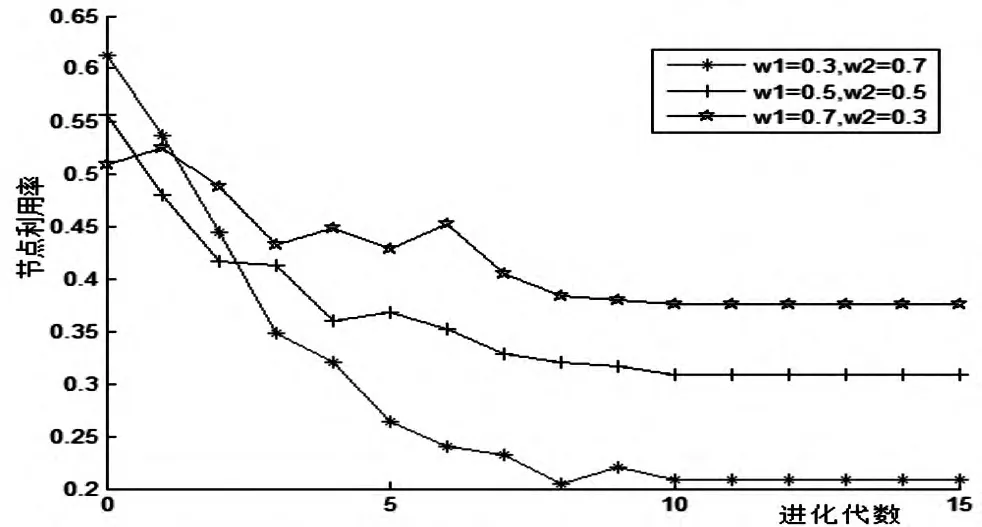
图4 权重对节点利用率的影响图

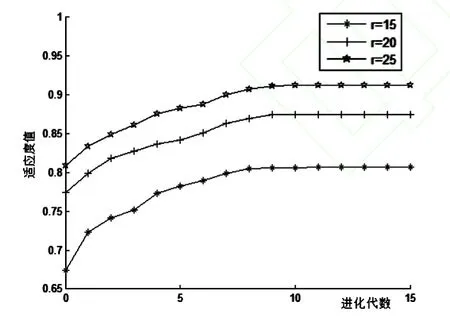
图5 感知半径对适应度的影响图

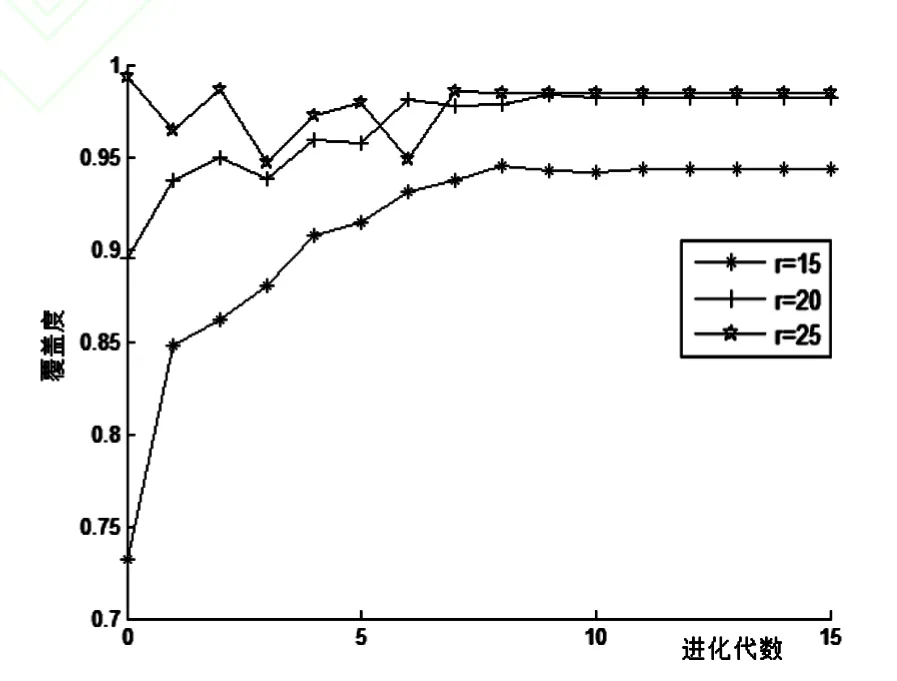
图6 感知半径对覆盖率的影响图

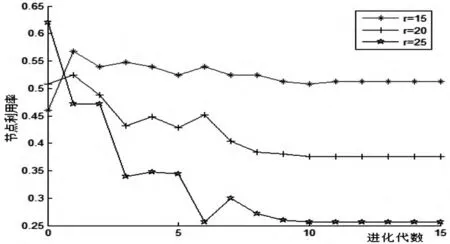
图7 感知半径对节点利用率的影响图

3.3 实验三

假设区域内有200个随机感知点,有100个传感器随机可行点,若感知点在传感器的覆盖范围内,则此感知点被覆盖,如何在可行放置点上部署最少数量的节点,使得所有感知点都被覆盖而任两个节点间的距离不小于距离阈值.如何通过调整节点的感知半径实现能量高效覆盖.

令w1=0.4,w2=0.6,在100×100的区域内部署,感知半径为10.图8为150个传感器全部开启时的覆盖情况,图9～10分别为第10、25代优化传感器覆盖图.图11为适应度、覆盖率及节点利用率的进化轨迹.

图8 150个传感器全部开启时的覆盖情况

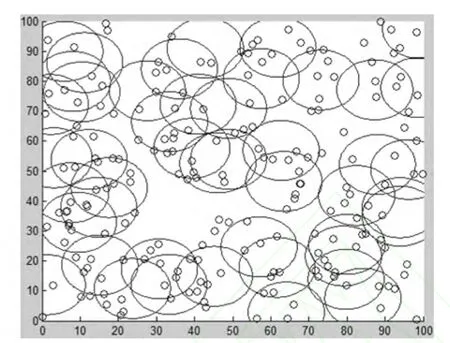
图9 第10代传感器覆盖图

图10 第25代传感器覆盖图

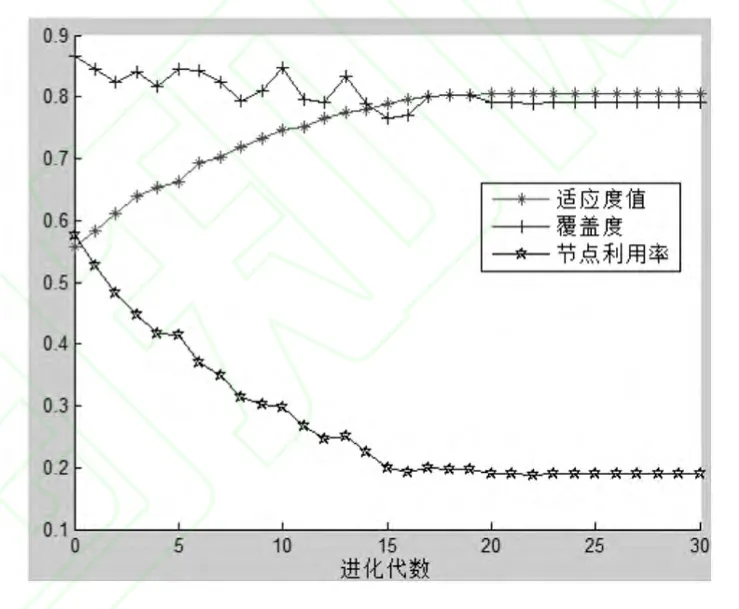
图11 三个函数的进化轨迹

由图11可知,最优解时覆盖率为0.7920,适应度为0.8051,节点利用率为0.1893,即用28个传感器,覆盖了200个被测点中的79.20%.

分析适应函数知,适应度最大为1(因为覆盖率理想值为1,节点利用率w1+w2=1),适应度越接近1,获得的解越接近最优解.

调节适应度函数中覆盖率和节点利用率权重,增加节点利用率的权重,即增大w2,减小w1,发现覆盖率会下降变差,节点利用率减小变好,同理,增大w1,减小w2,覆盖率会增大变好,节点利用率增大变差.

调节感知半径的大小,半径越大,每个传感器能覆盖更多的点,节点数越小,节点利用率降低,因此,当半径增大时,为了满足要求,求得最优适应解的权重w2要增大.同理,当半径减小时,w2也要适当减小.

当感知半径扩大为原来的2倍,即r=20时,实验发现,w2=0.7时覆盖率为0.9310,适应度为0.8925,节点利用率为0.1240.即只用12个传感器,覆盖率达到93.1%,结果最理想,见图12.

当r=25时,若仍取w2=0.7,覆盖率为0.98,节点利用率为0.10,适应度为0.924.若取w2=0.75,则覆盖率达到0.99,节点利用率仍为0.10,适应度为0.925,后者好于前者.实验结果见图13.

4 结论

对于本文算法所求解的问题,本文所描述的算法可以收敛于全局最优解.统计多次实验结果表明,覆盖率函数的权重增加,会引起求解出的最优工作节点集覆盖率增加,总体适应度增加,同时造成该节点集的节点利用率增加,传感器节点数目增多;对于传感器节点总数相同的传感器网络冗余覆盖,若传感器感知半径越大,则进化所得最优工作节点集工作传感器节点数目更少,从而实现更好的网络覆盖质量;此外,在原始算法中采用精英保留策略,可以加快收敛速度,同时能够改进收敛结果.

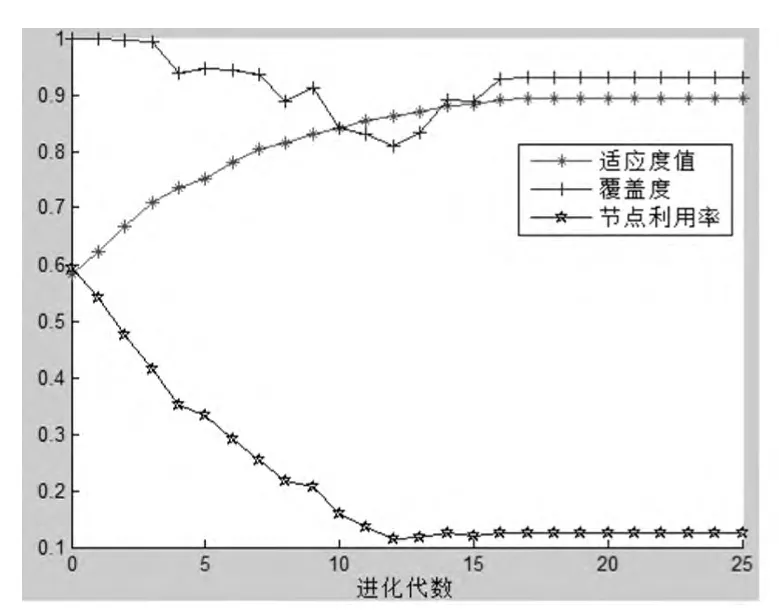
图12 r=20时,三个函数的变化轨迹

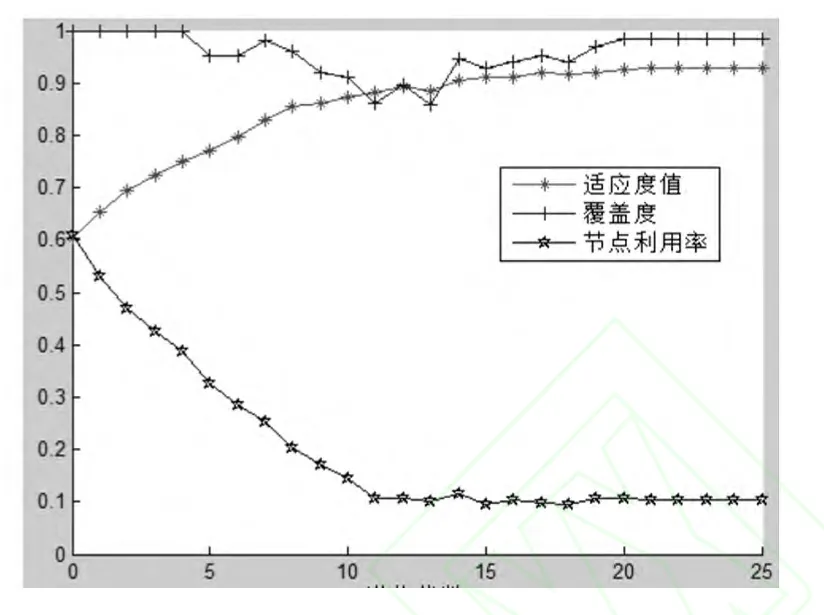
图13 r=25时三个函数的变化轨迹

[1]任丰原,黄海宁,林闯.无线传感器网络 [J].软件学报,2003,14(7)：1282-1291.

[2]班庆奇,陈志刚.无线传感器网络覆盖和连通问题概述 [J].电脑与信息技术,2010,18(03)：39-40.

[3]王伟,林锋,周激流.无线传感器网络覆盖问题的研究进展 [J].计算机应用研究,2010,27(01)：32-35.

[4]吕广辉,崔逊学,侯战胜.一种基于遗传算法的无线传感器网络覆盖模型 [J].微型机与应用,2010,29(15)：59-62.

[5]张西红,妙文亮,高彦彦.无线传感器网络的覆盖问题研究 [J].计算机工程,2009,35(16)：109-111.

[6]ZHANG Q.On stability of fixed point of li mit models of univariate marginal distribution Part 1,binry parameter[J].lecture notes in co mputer science.Berlin,Ger many：Springer-Verlag,1996,1141,Parallel Problem Solving from Nature-PPSN：178-187.

[7]ZHANG Q,Mühliebei H.On t he convergence of class of esti mation of distribution algorit h ms[J].IEEE Trans on Evolutionar y Co mputation,2004,8(2)：127-136.

[8]周树德,孙增圻.分布估计算法综述 [J].自动化学报,2007,33(2)：113-124.

[9]贾杰,陈剑,常桂然,赵林亮,王光兴.无线传感器网络中基于遗传算法的优化覆盖机制 [J].控制与决策,2007,22(11)：1289-1292,1301.

[10]郭小清,谢忠红.无线传感器网络覆盖性能研究 [J].计算机科学,2011,38(10 A)：364-366.

[11]HONGHAI ZHANG,JENNIFER C HOU.Maintaining sensing coverage and connectivity in large sensor net wor ks[J].Wireless Ad Hoc and Sensor Net wor k,2005,1(1)：89-124.

[12]毛茑池,陈力军,陈道蓄.无线传感器网络覆盖控制技术研究 [J].计算机科学,2007,34(3)：20-22.

[13]KUMAR S,LAI T H,BALOGH J.On k-Coverage in a Mostly Sleeping Sensor Net wor k[C].Proceedings of ACM MOBICOM,2004.

[14]景勃,孙勇,张劼.智能网络传感器与无线传感网络[M].北京：国防工业出版社,2011.

[15]HHANG C F,TSENG Y C.The Coverage Proble min a Wireless Sensor Net wor k[J].Mobile net nor ks and applications,2005,10：519-528.