置换Sb的M(=Bi,Te)掺杂β-Zn4Sb3对Seebeck系数的影响

刘雅洁

(嘉兴学院 南湖学院,浙江嘉兴314001)

近年来,随着世界能源危机的加剧和人们环保意识的提高,寻找高效率、无污染的新能源已成为人们越来越感兴趣的课题.半导体热电材料是将热能与电能直接转换的功能材料,其在工业余热、废热发电和半导体制冷领域中的运用持续受到极大关注.[1-5]特别是Zn4Sb3基的化合物在热电应用领域吸引了更多关注,[6-9]这是因为在中温区 (473-673 K),这种材料具有独特的低热导率和超常的热电性质.尽管Zn4Sb3至少存在4种晶相,但只有β相表现出高热电特性.[10]热电材料的性能通常用无量纲热电优值 (ZT)的高低评判,其定义式ZT=α2σT/λ,式中α是Seebeck系数,σ是电导率,λ是热导率,T是绝对温度.β-Zn4Sb3材料的ZT最大值可达到1.3,[6,11]无毒且相对便宜,因此,具有潜在的商业价值.

可通过提高Seebeck系数和电导率,降低热导率的方法来提高热电优值.但这些参量并不可以独立控制,比如,热导率与电导率通过Wiedemann-Franz定律紧密相关.为了提高热电优值,必须采取有效手段在降低晶格热导率的同时保持良好的电导特性.β-Zn4Sb3被认为是声子玻璃电子晶体材料 (phonon glass-electr on),是在化学式为Zn13Sb10的材料中无序而弥散地分布的一些Zn原子构成.通过光子散射,声子平均自由程显著降低,导致其热导率降低.[7]因此,Zn的多少直接影响着β-Zn4Sb3的热电性能.[12-13]同时,β-Zn4Sb3材料合成条件苛刻,材料脆性大,故样品不易制备.对此,利用掺杂对其进行改性,可进一步优化其成分和结构,提高其热电性能.[14-18]

β-Zn4Sb3是二元材料,掺杂原子M可置换Zn或Sb元素构成名义组成为β-(Zn1-xMx)4Sb3或β-Zn4(Sb1-xMx)3的材料.[14-18]置换的情况不同,材料的热电性能也不相同.到目前为止,对这两类材料的讨论大多停留在材料制备和热电性能测量方面,对热电材料的重要参量Seebeck系数也只是给出其与温度的曲线关系,几乎未定量研究.曾有文献研究了一些(Zn1-xMx)4Sb3类材料Seebeck系数与温度的定量关系,得到一些有意义的结果.[19]目前,还没有文献讨论Zn4(Sb1-xMx)3类材料Seebeck系数与温度的定量关系.本文拟讨论两种材料——Zn4(Sb1-xMx)3(M=Bi,Te)的Seebeck系数与温度的定量关系,找寻Seebeck系数α的峰值αmax及对应的温度Tc.

1 数据及其讨论

两种Zn4(Sb1-xMx)3M(=Bi,Te)的Seebeck系数与温度的关系如图1所示,所有数据通过对实验数据进行回归分析获得.[17-18]

由图1不难看出,(M=Bi,Te)掺杂的β-Zn4Sb3的Seebeck系数是随着掺杂量和温度有规律地变化.寻求这种变化定量关系会对热电材料的制备以及进一步研究热电材料的热电优值带来很大方便.理论上说,通过对材料建立相应的物理模型,经过理论或数值计算有可能得到与实验结果相吻合结论.但是,Zn4Sb3材料结构较复杂,在实验过程中还发现会部分出现由β相到α相的变化,[20]因此,建立一个合理模型进行理论计算成为一种近乎不可能完成的事情.按照霍姆亥兹的观点：如果经过某种途径找到一个与实验结果相当好地符合的函数,那么这个函数很可能是唯一、正确描述实验现象的数学表达.因此,如果能够找到Seebeck系数与温度的之间满足的函数关系,或许是一种合理的方法.

图1 (M=Bi,Te)掺杂热电材料β-Zn 4 Sb 3的Seebeck系数随温度的变化关系

图1中,9条曲线有两个共同特点：第一,每条曲线有一个峰值温度Tc,对应材料最大的Seebeck系数αmax,掺杂量不同,峰值温度Tc和对应的最大Seebeck系数αmax是不同的;第二,所有Seebeck系数均为正值,说明载流子类型是P型.显然,第一个特点最值得关注.通过分析图1给出的9条曲线,发现高斯函数可以精确表示图1给出的实验关系,表达式如下：

这里,α1、α2、Tc和w都是与材料相关、待优化的参数.当T=Tc时,αmax=α1+α2.按照 (1)式给出的关系,对图1所有情况进行分析,得到了不同情况下峰值温度Tc,列于表1中.同时,为了说明 (1)式给出方法与实验结论的吻合程度,在表1中同时列出相关系数 (R)和平均相对误差(ARE=是实验数据,α是计算数据).在表1中,最小的相关系数为0.998 59,最ic大的平均相对误差为0.35%,说明模型 (1)给出的拟合结果与实验数据符合得非常好,其结果如图2所示.良好的结果说明,在分析 (M=Bi,Te)掺杂的β-Zn4Sb3的Seebeck系数随温度及掺杂量的关系问题上,我们提出的这种方法应该是一种好方法.

表1 含有不同比列的M(=Bi,Te)掺杂β-Zn 4 Sb 3的Seebeck系数随温度的变化关系

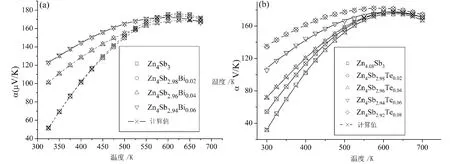
图(M=Bi,Te)掺杂热电材料β-Zn 4 Sb 3的Seebeck系数随温度的2变化关系的实验数据 (图中散点)与模型 (1)的理论计算 (图中相应的-×-)的比较

由表 (1)可知,其峰值温度Tc并不随着掺杂量的增加而增加.Bi掺杂时,其峰值温度Tc随着掺杂量的增加先增加而后减少,但Te掺杂时,峰值温度Tc随着掺杂量的增加而减少.这说明掺杂元素不同,对Seebeck系数的影响是不同的.对峰值温度Tc随掺杂量的变化进行研究,没有发现实质性的规律,这是实验数据不足的结果.但过量Zn会导致峰值温度Tc升高,对应的Seebeck系数最大值αmax=α1+α2增加,这个结论在已有文献[12-13]没有看到.过量Zn确实会导致Seebeck系数在一些温度区间降低 (见图1或图2的Zn4Sb3和Zn4.08Sb3曲线),这个结果与文献[12-13]的结果相同.至于Seebeck系数的量值与文献[12-13]不同,说明不同实验小组的材料存在一定的差别 (本文数据取自同一实验小组).

当以β-Zn4Sb3的Seebeck系数为自变量、以掺杂材料的Seebeck系数作为因变量得到置换掺杂材料的Seebeck系数与基体材料Zn4Sb3的Seebeck系数之间的关系,如图3所示.图3表明,低温区(β-Zn4Sb3的Seebeck系数较小处)通过掺杂可改善材料的Seebeck系数;但在高温区掺杂后,材料的Seebeck系数变化不明显.

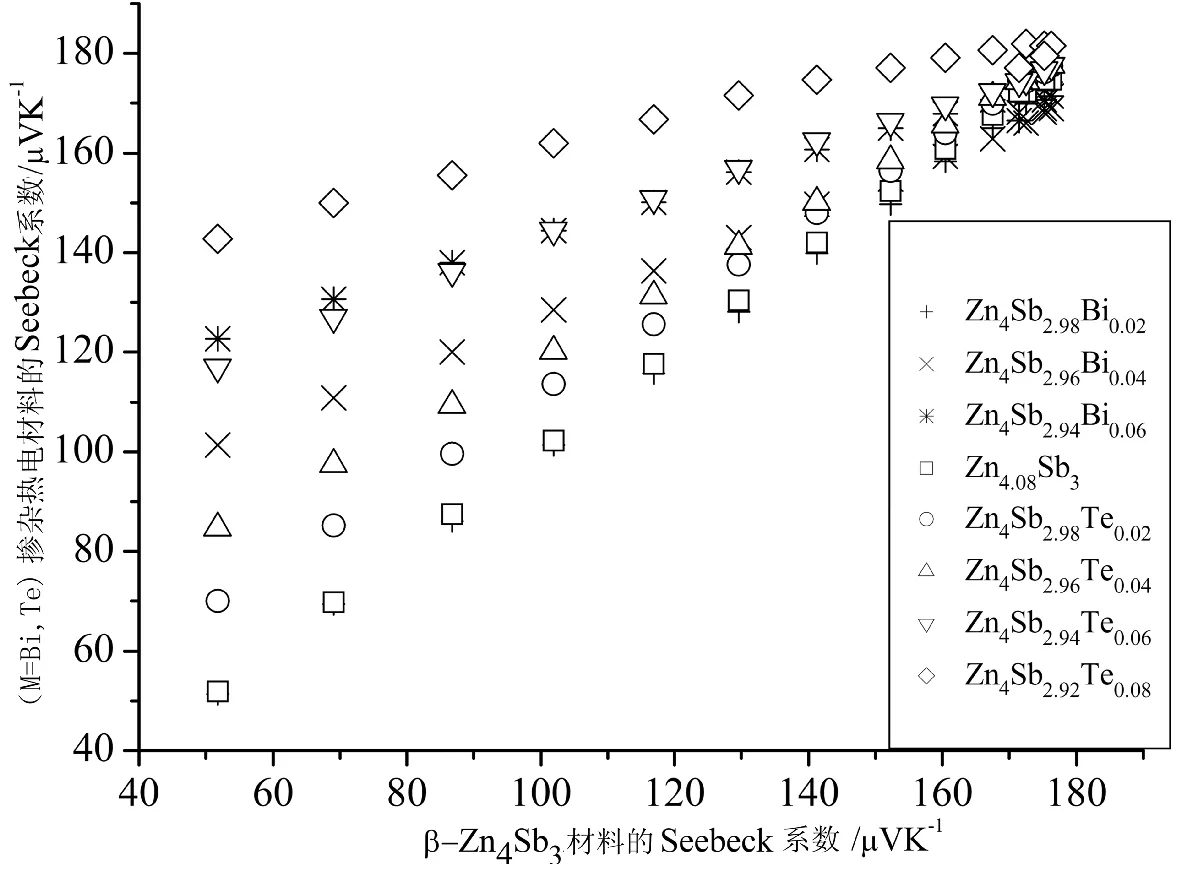
图3 (M=Bi,Te)掺杂热电材料的Seebeck系数与β-Zn 4 Sb3材料的Seebeck系数实验的关系图

2 结论

人们通过实验寻求各物理量之间的依赖关系,通过分析实验结论找寻物理量的数量关系,为发展、丰富物理学理论而努力.本文的工作就是基于后一种情况进行.

本文讨论了Sb置换M(=Bi,Te)掺杂热电材料β-Zn4Sb3材料的Seebeck系数随温度的变化规律,找到了掺杂量x不同时的Seebeck系数随温度变化的准确定量关系——高斯函数,为研究热电材料性能提供了线索.通过数据比较发现,所有的拟合结果与实验所测数据非常吻合,最大平均相对误差为0.35%,相关系数均达到0.998 59以上.

定量讨论实验规律是必要的科学研究方法之一.对热电材料的Seebeck系数随温度的变化规律进行物理建模,再进行计算是一件困难的、甚至是不可能完成的工作,这是因为材料太过复杂的原因.因此,采用数据拟合的方法给出实验规律,不失为一种可行的方法,其结果对实验研究、理论研究有一定的指导意义.

[1]LYEO HO-KI,KHAJETOORIANS A A,LI SHI,et al.Profiling the ther moelectric power of semiconductor junctionswit h nano meter resolution[J].Science,2004,303(5659)：816-818.

[2]TAKASHIRI M,TANAKA S,TAKIISHI M,et al.Preparation and characterization of Bi0.4 Te3.0Sb1.6 nanoparticles and t heir t hin fil ms[J].J.Alloys Co mpd.,2008,462(1)：351-355.

[3]SHAKOURI A.Recent develop ments in se miconduct or t her moelectric physics and materials[J].Annu.Rev.Mater.Res.,2011,41(1)：399-431.

[4]SOOTSMAN J R,CHUNG D Y,KANATZIDIS M G.New and old concepts in t her moelectric materials[J].Angew.Che m.-Int.Edit.,2009,48(46)：8616-8639.

[5]CLINGER L E,PERNOT G,BUEHL T E,et al.Ther moelectric properties of epitaxial Tb As：In Ga As nanoco mposites[J].J.Appl.Phys,2012,111(9)：094312-094312-5.

[6]CAILLAT T,FLEURIAL J P,BORSHCHEVSKY A.Preparation and t her moelectric properties of semiconducting Zn4Sb3[J].J.Phys.Che m.Solids,1997,58(7)：1119-1125.

[7]SNYDER G J,CHRISTENSEN M,NISHIBORI E,et al.Disor dered zinc in Zn4Sb3wit h phonon-glass and electr oncrystal t her moelectric properties[J].Nat.Mater.,2004,3(7)：458-463.

[8]LITVINCHUK A P,NYLEN J,LORENZ B,et al.Optical and electr onic pr operties of t her moelectric Zn4Sb3acr oss t he low-te mperature phase transitions[J].J.Appl.Phys,2008,103(12)：123524-123524-6.

[9]BOULET P,RECORD M C.Str uct ural investigation of t he Zn1-xCdxSb solid solution by density-f unctional t heor y approach[J].Solid State Sci.,2010,12(1)：26-32.

[10]MOZHARIVSKYJ Y,PECHARSKY A O,Bud＇ko S,et al.A pro mising ther moelectric material：Zn4Sb3or Zn6-δSb5.Its co mposition,structure,stability,and poly morphs.Structure and stability of Zn1-δSb[J].Chem.Mater.,2004,16(8)：1580-1589.

[11]CHITROUB M,BESSE F,SCHERRER H.Ther moelectric properties of semi-conducting compound Zn4Sb3[J].J.Alloys Compd.,2008,460(1)：90-93.

[12]祁琼,唐新峰,熊聪,等.过量Zn对β-Zn4Sb3热电性能影响的研究 [J].物理学报,2006,55(10)：5539-5544.

[13]张敏,刘昶时.4种含Zn复合材料Seebeck系数之间的关系 [J].嘉兴学院学报,2011,23(3)：47-52.

[14]NAKAMOTO G,SOUMA T,YAMABA M,et al.Ther moelectric properties of(Zn1-xCdx)4Sb3below room temperature[J].J.Alloys Compd.,2004,377(1)：59-65.

[15]PEDERSEN B L,BIRKEDAL H,NYGREN M,et al.The effect of Mg doping on the ther moelectric perf or mance of Zn4Sb3[J].J.Appl.Phys.,2009,105(1)：013517-013517-6.

[16]PAN L,QIN X Y,XIN H X,et al.Enhanced ther moelectric properties of iron doped co mpound(Zn1-xFex)4Sb3[J].Inter metallics,2010,18(5)：1106-1110.

[17]ZHOU L,LI W,JIANGJ,et al.Effect of Bi doping on the ther moelectric properties of Zn4Sb3[J].J.Alloys Co mpd.,2010,503(2)：464-467.

[18]LI W,ZHOU L,LI Y,et al.Ther moelectric properties of hot-pressed Zn4Sb3-xTex[J].J.Alloys Co mpd.486(2009)335-337.

[19]刘雅洁.M(=In,Al,Cd)掺杂对Zn4Sb3热电材料Seebeck系数的影响 [J].嘉兴学院学报,2012,24(3)：98-101.

[20]LI D,QIN X Y.Effects of Te doping on the transport and ther moelectric properties of Zn4Sb3[J].Inter metallics,2011,19(11)：1651-1655.