建构主义理论指导下的初中几何图形变换模型教学策略研究
孙丹

摘 要:数学建模是一种主动建构的过程,体现了创造性,数学建模能力就是创新能力的具体体现。因此本文以建构主义理论为指导,探究几何图形变换模型教学的有效策略。
关键词:建构主义;几何图形;策略
一、建构主义基本理论
建构主义理论提倡在教师指导下的以学习者为中心的学习,教师是意义建构的帮助者、促进者,而不是知识的传授者与灌输者。
二、几何图形变换的教学策略分析
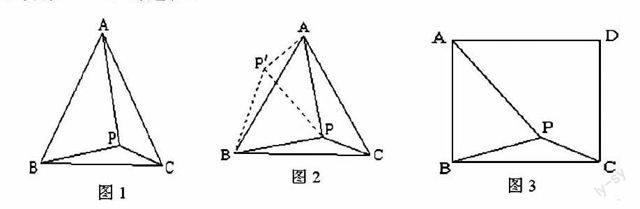
【例1】(阅读理解式的几何模型问题),如图1,在等边三角形ABC内有一点P,且PA=2,PB=3,PC=1.求∠BPC度数的大小和等边三角形ABC的边长.甲同学的思路是:将△BPC绕点B顺时针旋转60°,画出旋转后的图形(如图2)然后求解。如图3,在正方形ABCD内有一点P,且PA=5,BP=2,PC=1.求∠BPC度数的大小和正方形ABCD的边长。
学生在遇到这样的问题时,通常学生会认为无从下手,但是这时教师首先要树立学生的自信心,从题目所给材料出发,寻找建立模型的突破口。材料中小明的做法是通过图形的旋转来解决问题的,关键是旋转的角度是60度,此时教师要重点向学生提出质疑:为什么旋转的是60度?如果旋转的是30度、45度又会如何?引导学生主动发现旋转60度的玄机就是:题目中原来大图形是等边三角形,需要用60度去构造另一个等边三角形。此时,教师注意引导学生观察所求的问题中原图形是有什么特征的图形,旋转角度定为多少才更合适?学生自己观察会发现,所求题目中原图是一个正方形,这样只有旋转90度才能成功构造一个直角三角形,从而解决问题。
解:如图,将△BPC绕点B逆时针旋转90°,得△BP′A,则△BPC≌△BP′A。
∴∠BPC=∠AP′B=135°。得AB=5。即∠BPC=135°,正方形边长为5。
对于一些材料问题,大部分学生将实际问题转化为数学问题的能力偏低,教师必须要教会学生通过阅读理解根据自己的建构准确地将文字语言转化为数学符号语言,这一点恰恰是教学的一个盲点,学生即使阅读了问题,也没有办法将文字语言转化为数学语言,这要求教师在课堂教学中要注意指导学生在阅读中通过想象、联想、思考等活动将阅读的内容与所学知识联系到一起,坚持不懈地训练,学生一定会养成良好的阅读理解能力。笔者在读期间一直做中学数学家教,曾经教过初一到初三16个学生,这16名学生基础参差不齐,有期末考试可以得115分的高分學员有只靠42分的后进生学员,但是他们大多数存在一个问题,就是不愿意做阅读类题目,当遇到阅读信息题,或者是探究类题目时会在没有做题前就产生抵触情绪,宁可多做几道纯数学题。甚至在阅读期间由于字太多不能理解而被气哭了,但是事后我们曾经交流过这样的原因:学生说,她读不懂是什么意思,不知道那么多字是什么意思,即使读了也不明白和以前学习过的知识有什么联系,不知道从何下手,不会提取文字中的信息,好胜心强就被气哭了。这位学生就是得115分的高分生,在这之后我也让其他的学员练习了这道题,但是他们都说老师太长了,考试不能考,再说了我这样的水平只要做简单的题就行了,这么难的题我不会也可以的。
学生没有尝试就直接放弃了,这其中有太多的问题存在,有学生对自己能力的否定,当然也有学生学习的惰性,但是更多地是学生对阅读类题目的陌生,学生通常认为考试不会出这样的题,应试教育导致了建模课程的开展困难,因此教师必须要端正学生学习的态度,加强学生阅读能力。在解决问题时,只有理解了题目的内容,才能真正解决它,才会更自主去学习数学知识。教师在进行几何图形变换教学时,教师应该加强课本教材的钻研、为学生创设自主建构学习情境、培养学生几何图形转换能力、注重发展学生的非智力因素。
(作者单位:延边大学理学院)
参考文献:
[1] 教育部.义务教育数学课程标准[M].北京:北京师范大学出版社,2012
[2] 邵东生.中学数学建模教学研究与实践[D].福州:福建师范大学,2001
[3] 颜俐.数学建模教学设计原则[J].柳州师专学报,2002(02)
[4] 白兴波.数学建模与中学生研究性学习能力的培养[J].江西金融职工大学学报,2006(S2)
[5] 郑燕捷,叶雪梅.课标课程下中学数学建模的教学实践与思考[J].中国科教创新导刊,2010(12)

