利用卫星测高、GRACE和GOCE资料估计全球海洋表面地转流

冯贵平，金双根，Jose M.Sanchez Reales

（1.上海海洋大学海洋科学学院，上海201306；2.中国科学院上海天文台，上海200030；3.University of Alicante，Alicante，Spain）

利用卫星测高、GRACE和GOCE资料估计全球海洋表面地转流

冯贵平1，2，金双根2*，Jose M.Sanchez Reales3

（1.上海海洋大学海洋科学学院，上海201306；2.中国科学院上海天文台，上海200030；3.University of Alicante，Alicante，Spain）

重力恢复和气候试验GRACE（gravity recovery and climate experiment）卫星极大地提高了地球重力场的精度和分辨率，特别是中长波分量，联合卫星测高数据可获得全球海洋表面大尺度洋流循环。另外，新一代地球重力和海洋环流探测卫星GOCE（gravity field and steady-state ocean circulation explorer）于2009年3月成功发射，采用卫星重力梯度测量原理，对重力场的高频部分非常敏感，使其高分辨率监测全球海洋循环成为可能。本文利用1～7年GRACE观测数据确定的重力场模型和18个月GOCE观测数据确定的地球重力场模型GO_CONS_GCF_2_TIM_R3，联合卫星测高确定的平均海面高模型MSS_CNES_CLS_11，分别估计全球海洋表面地转流，并且与实测浮标数据结果进行比较。分析表明GOCE重力卫星确定的重力场模型具有更高的空间分辨率，能够确定高精度和高空间分辨率的全球海洋地转流，如墨西哥湾暖流的细节和特征，并且与实测浮标结果基本一致。而基于1～4年GRACE观测资料的模型不能很好估计全球地转流特征，基于7年GRACE观测资料的重力场模型ITG-Grace2010s确定的全球地转流的精度仍低于18个月GOCE观测数据确定的地球重力场模型GO_CONS_GCF_2_TIM_R3的结果，估计的全球地转流仍含有较大的噪声，不能很好地反应中小尺度地转流细节特征。并计算ITG_Grace2010s和GOCE_TIM3的稳态海面地形和全球平均地转流的内符合精度，结果显示，在全球范围内，GOCE_TIM3的稳态海面地形和全球平均地转流的精度都比ITG_Grace2010s结果的精度有着很大的改善，其中ITG_Grace2010s的稳态海面地形的精度为21.6 cm，而GOCE_TIM3的结果则为7.45 cm，ITG_Grace2010s的全球平均地转流的精度为40.7 cm／s，而GOCE_TIM3的结果则为19.6 cm／s。

地转流；GOCE；GRACE；卫星测高

1 引言

海面地形通常定义为平均海面高与大地水准面高度之差，其中包含洋流动力学信息。洋流是一种主要的海洋动力学现象，对于研究和理解气候模式、海洋热量的传递、海水质量的变迁、全球能量的传输与交换以及海洋、陆地和大气之间的相互作用有着非常重要的科学意义。因此，精确确定海面地形和海洋环流及其动力学特征，一直是气象学家、海洋学家、地球物理学家以及海洋从业人员研究的热门方向。目前海洋洋流分为三类：（1）相对于海洋密度分布的正压和斜压地转洋流，简称地转流；（2）风驱动洋流；（3）潮汐洋流和内波洋流。其中地转流和潮汐洋流与海面高度密切相关［1］，本文主要讨论地转流。地转流是指在不考虑摩擦力和大气压力的作用时，水平压强梯度力与科里奥利力相互平衡状态下的稳定洋流，通过将海面地形数据代入地转平衡方程可得到全球表面地转流。因此，获得高精度、高分辨率地转流的关键是要获得高精度的海面地形。

传统的海面地形估计主要是利用实测海洋温度和盐度数据，这种方法需要定义一个“无运动”或“已知运动”状态的平面，并且由于实测数据稀少和季节性偏差等因素，使得该方法无法精确地估计海面地形。随着近20年卫星测高卫星技术的发展，从最初的Topex／Poseidon到最新的Jason-2卫星，已经积累了大量的海面观测数据。卫星测高技术具有独特的全天候、长时间、大面积和高精度等优点，克服了传统海洋测量数据采集的缺点。利用这些观测数据，可以得到高时空分辨率的平均海面高。而传统方法观测得到的重力场模型存在较大不确定性，并且融入了卫星测高的数据，因此无法得到高精度和高分辨率的大地水准面。受大地水准面精度的限制，高分辨率高精度的海面地形一直无法获得。卫星重力测量技术的出现为全球高覆盖、高分辨率和高精度的重力观测开辟了新的途径，使得高精度和高分辨率地球重力场的确定成为可能。2000年7月15日德国发射“挑战微型卫星有效载荷”（CHAMP）卫星，开创了卫星重力学研究的重要先河，随后由美国NASA和德国DLR于2002年3月发射低低卫－卫跟踪“重力恢复与气候试验”（GRACE）卫星。GRACE采用低低轨道卫—卫跟踪技术，距离变化率以微米级K波段测距仪实时测得，其距离变化率可反演重力场信息。因此，GRACE卫星重力提供的地球月变重力场信息可以用于研究海面地形以及大尺度海洋循环［2—4］。联合现有卫星重力GRACE和卫星测高数据探测的全球平均地转流，在大、中尺度上与海洋学结果相一致，却很难探测中小尺度的海洋表面地转流特征［5］。

最近欧洲航天局研制的新一代“地球重力和海洋环流探测”（GOCE）卫星于2009年3月成功发射。GOCE的卫星轨道与太阳同步，轨道高度约为260 km，轨道倾角为96.5°。GOCE采用高低卫—卫跟踪模式，利用卫星重力梯度测量原理，其携带的高精度三轴重力梯度仪分别测定沿迹向、法向和径向重力梯度值，直接用卫星梯度仪测量低轨卫星重力位的二阶导数反演出地球重力场，并且GOCE卫星轨道较低，有利于反映短波长高阶重力场。另外，GOCE利用重力梯度测量，消除了非保守力加速度的影响，使其对重力场的高频部分更加敏感。GOCE卫星的科学目标是在小于100 km空间尺度上获得1～2 cm精度的大地水准面及其海洋应用［6］。

本文利用1～7年GRACE观测资料和18个月GOCE观测数据得到的高精度和高空间分辨率重力场模型确定的高精度大地水准面，结合卫星测高数据得到的平均海面高数据估计和分析全球海面动力地形与表面地转流及其特征，并与实测浮标结果以及联合GRACE／CHAMP／GOCE的相应结果进行比较和分析。

2 地转流估计理论与方法

2.1 大地水准面的确定

高精度重力场模型是精确确定大地水准面的基础。GRACE观测从2002年8月继续到现在，目前有多种基于GRACE观测资料的重力场模型，本文中主要采用了由Mayer-Gürr等人利用2002年8月到2009年8月近7年的GRACE观测数据解算得到的重力场模型ITG_Grace2010s，模型的最高阶次为180［7］。而GOCE重力场模型则利用Pail等人用2009年11月到2011年4月GOCE观测数据所解算的250阶地球重力场模型GO_CONS_GCF_2_TIM_ R3（http：／／icgem.gfz-potsdam.de／ICGEM）［8］。利用重力场模型可计算大地水准面：

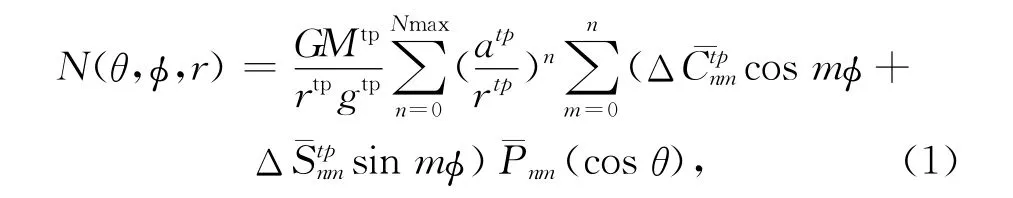
式中，（θ，φ，r）分别为地心余纬、经度和地心距；GM为地球总质量乘以万有引力常量，a参考椭球的赤道半径，g重力常数；（ΔC，ΔS）是无量纲正则化的球谐系数；¯P是正则归一化的缔合勒让德系数。上标tp表示相对于Topex／Poseidon基准椭圆［9—10］。

由上式可分别计算出GRACE和GOCE所确定的静态大地水准面（相对于T／P基准椭圆），都截断至180阶球谐系数。图1表示由GRACE和GOCE分别确定的大地水准面，其中图1a表示GRACE确定的大地水准面，图1b表示GOCE确定的大地水准面，图1c表示两者确定的大地水准面高之差（空间分辨率0.25°×0.25°），可见两者确定的大地水准面仍存在着较大差异，在海岸沿线等区域达到了2 m。

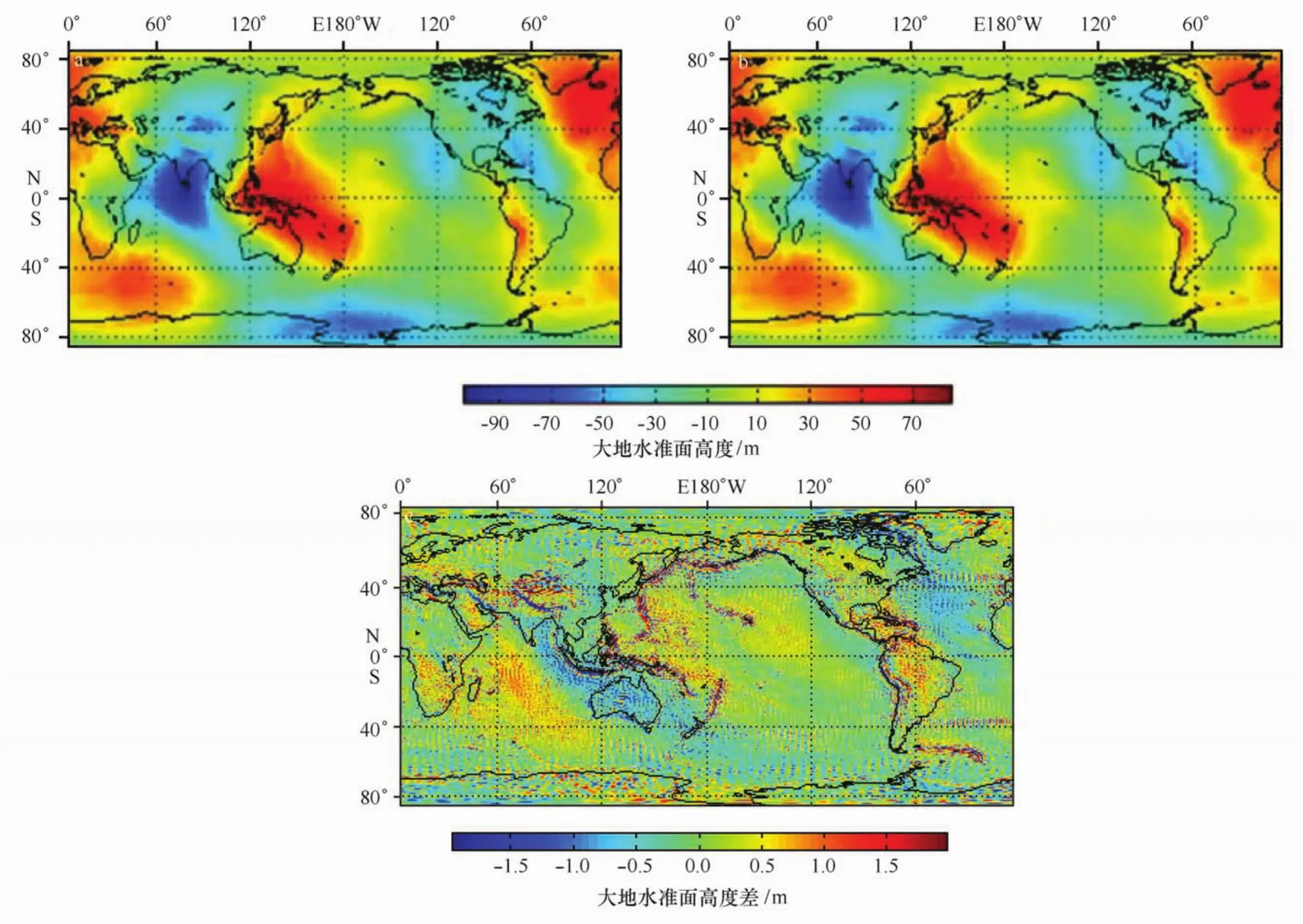
图1 GOCE与GRACE重力场模型确定的大地水准面高及其两者之差Fig.1 Comparison of geoid height from GOCE and GRACE gravity models

2.2 平均海平面高的确定

卫星测高技术能够提供精确的全球海面高度。本文利用平均海面高模型MSS_CNES_CLS_11确定平均海面高度（MSS），该模型是由AVISO（Archiving，Validation and Interpretation of Satellite Oceanographic Data）在2011年7月发布的（http：／／www.aviso.oceanobs.com）。平均海面高模型MSS_CNES_ CLS_11融合了10年的Topex／Poseidon测量数据，8年的ERS-1／2测量数据，7年的Geosat测量数据，7年的Envisat测量数据和7年的Jason-1测量数据进行估算［11］。MSS_CNES_CLS_11模型定义的平均海面高是在80°S～84°N之间，空间分辨率为2′×2′。为了与大地水准面结合，选取与大地水准面相同的格网点，得到全球平均海平面高的0.25°×0.25°格网数据。

2.3 海面地形和地转流的确定

海面地形（MDT）是平均海面高（MSS）与大地水准面高（N）之差，可表示为：

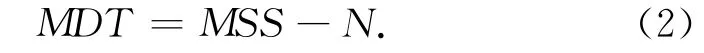
稳态海面地形为参考时间段内平均海平面相对于大地水准面的偏差。需要注意的是，平均海平面高和大地水准面高所采用的参考椭球和潮汐系统必须一致［12－13］，本文选择Topex／Poseidon参考椭球和平均潮汐系统。根据已经计算得出的大地水准面高和平均海平面高，可以确定稳态海面地形。由于平均海面高是空间格网形式并且只定义在海洋上，而且它的空间分辨率高于大地水准面高，从而在计算稳态海面地形时需要把它们统一到同一尺度下。本文是先是将2′×2′的平均海面高模型内插值为0.25°×0.25°，其次将海面高模型的陆地区域，用格网化的大地水准面高代替，对综合后的海面高在球域内作球谐展开，让其展开至与N同阶次［13—14］，再次为了进一步削弱高频噪声，用高斯滤波方法对二者在频域内进行同样的滤波处理［15—16］，最后，将滤波后的海面高系数减去相应阶次的重力场模型系数，得到稳态海面地形的球谐系数，并转化为格网形式。

除赤道和海岸地区外，长时间大规模的海水运动都处于地球自转平衡状态。在直角坐标系中（X轴向东为正，Y轴向北为正，Z轴向上为正，并与X，Y轴形成的右手坐标系），水平方向的科里奥利力与压强梯度力分量保持平衡，垂直方向的科里奥利力与压强梯度力分量及重力保持平衡。则将海面地形代入到地转平衡方程，即可得出地转流的速度［17］：

式中，u，v分别表示沿地球纬圈和经圈的流速，f＝2Ωsinφ是科里奥利参数，φ是纬度，Ω是地球自转角速度（视为常数），g是重力加速度。对于赤道地区地转流的计算方法可参考文献［18］。

3 结果与分析

将计算得出的稳态海面地形代入到公式（3）中，即可得出基于GRACE和GOCE重力场模型的全球平均地转流。图2表示基于GOCE重力场（GOCE_ TIM3）得到的全球海洋表面地转流，其中图2a和图2b分别表示了向东、向北方向的流速，图2c则表示地转流速率，图2d表示了速度的方向（以东向逆时针为正）。图3表示基于GRACE重力场模型（ITG_ Grace2010s）得到的全球表面地转流，矢量表示方法与图2一致。比较图2和3，可以明显地看出，基于GRACE、GOCE得到的全球平均地转流具有较好的一致性，能够反映出全球洋流的主要特征，如黑潮、南极绕极流、墨西哥湾流、厄加勒斯暖流、加利福尼亚流、巴西暖流和马尔维纳斯寒流等，且具有较高的时空间分辨率。表明GOCE和GRACE模型得到的大地水准面与卫星测高数据得到的高精度平均海面高能较高精度地估计全球地转流。但另一方面，两者也存在着差异，比较图2c和3c，可以发现GOCE确定的地转流条纹更加清晰，反映出更多的细节特征，而GRACE确定的地转流则含有较大的噪声，这一点在赤道区域反映的尤为显著，GRACE确定的地转流在赤道区域无法提取出有用信息，而GOCE的结果则能够很好的反映出南赤道流和北赤道流。

3.1 实测浮标数据的比较

为了检验GRACE和GOCE探测全球海洋表面地转流的能力和特征，将计算结果与浮标实测数据进行比较与分析。海洋表面的漂流浮标，其运动轨迹基本上反映了其所在位置的海洋表层流场，因此浮标数据能够真实地反映海洋表面流场的基本特征。美国国家海洋与大气管理局大西洋海洋学与气象学实验室（NOAA／AOML）通过对从1993—2012年的全球海洋表面所有漂流浮标的原始数据进行整合、质量控制和克里格插值法，提供了近乎全球空间范围内的全球表面流场［19—20］。漂流浮标观测数据包括潮流，地转流，埃克曼流，惯性流和高频非地转流。因此，为了和计算得到全球平均地转流进行比较分析，需要对海洋表面流场进行改正，消除其他海流的影响，得到全球地转流。将基于GOCE和GRACE重力场模型估计地转流结果与实测浮标结果进行比较，其标准差（RMS）为：

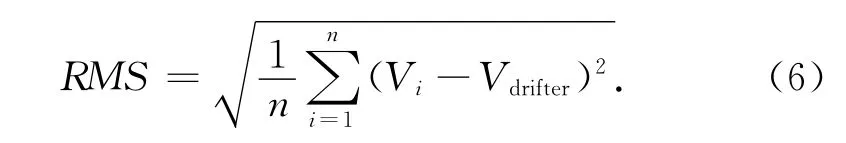
利用公式（6），分别计算了基于GOCE和GRACE重力场模型估计全球和5个主要的区域地转流（总的速率，纬圈分量和经圈分量）的RMS和相关系数（见表1）。表1表明，全球范围内，基于GOCE重力场模型得到的地转流和实测浮标结果有着更好的一致性，其RMS为17.47 cm／s，相关系数为0.46；而基于GRACE重力场模型得到的全球地转流的RMS则为20.38 cm／s，相关系数为0.41，特别是在经圈方向的相关性较差；在中、小区域中，基于GOCE重力场模型得到的地转流的RMS全都小于10 cm／s，其中南极绕极流的RMS仅为7.80 cm／s，而基于GRACE重力场模型得到的地转流的RMS均比GOCE的结果大1～2 cm／s，且与实测浮标数据的相关系数也都小于GOCE的结果。另外，对于基于GRACE和GOCE模型得到的地转流速，无论是在全球范围内，还是中、小区域中，其在纬圈方向上的分量的RMS明显小于经圈方向上的分量。上述分析表明，基于GOCE得到的全球地转流无论是在全球范围，还是在中、小区域内，都比基于GRACE得到的全球地转流，与浮标实测结果符合的更好，有着更高的相关性。

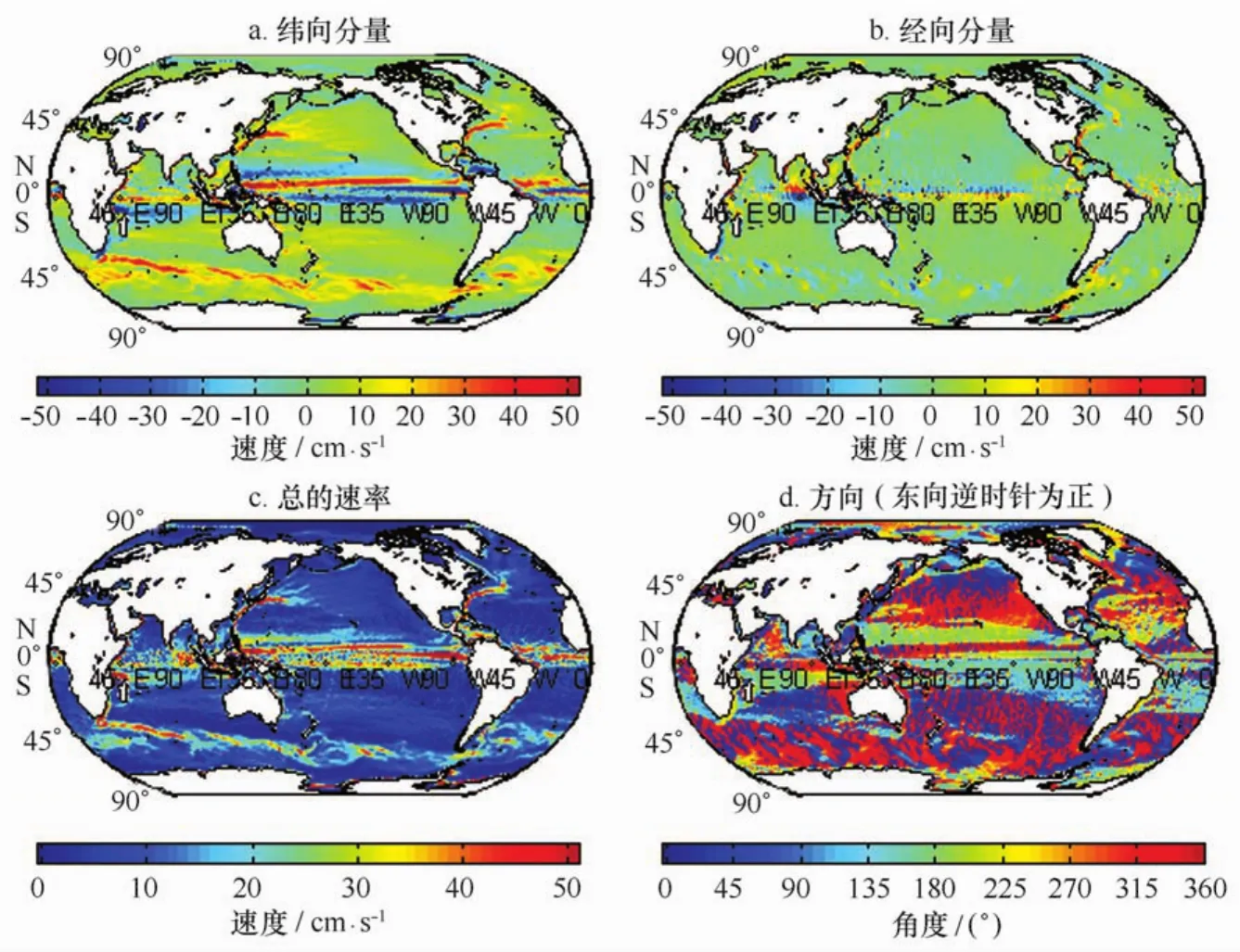
图2 GOCE得到的全球地转流Fig.2 Global ocean surface geostrophic currents predicted from GOCE

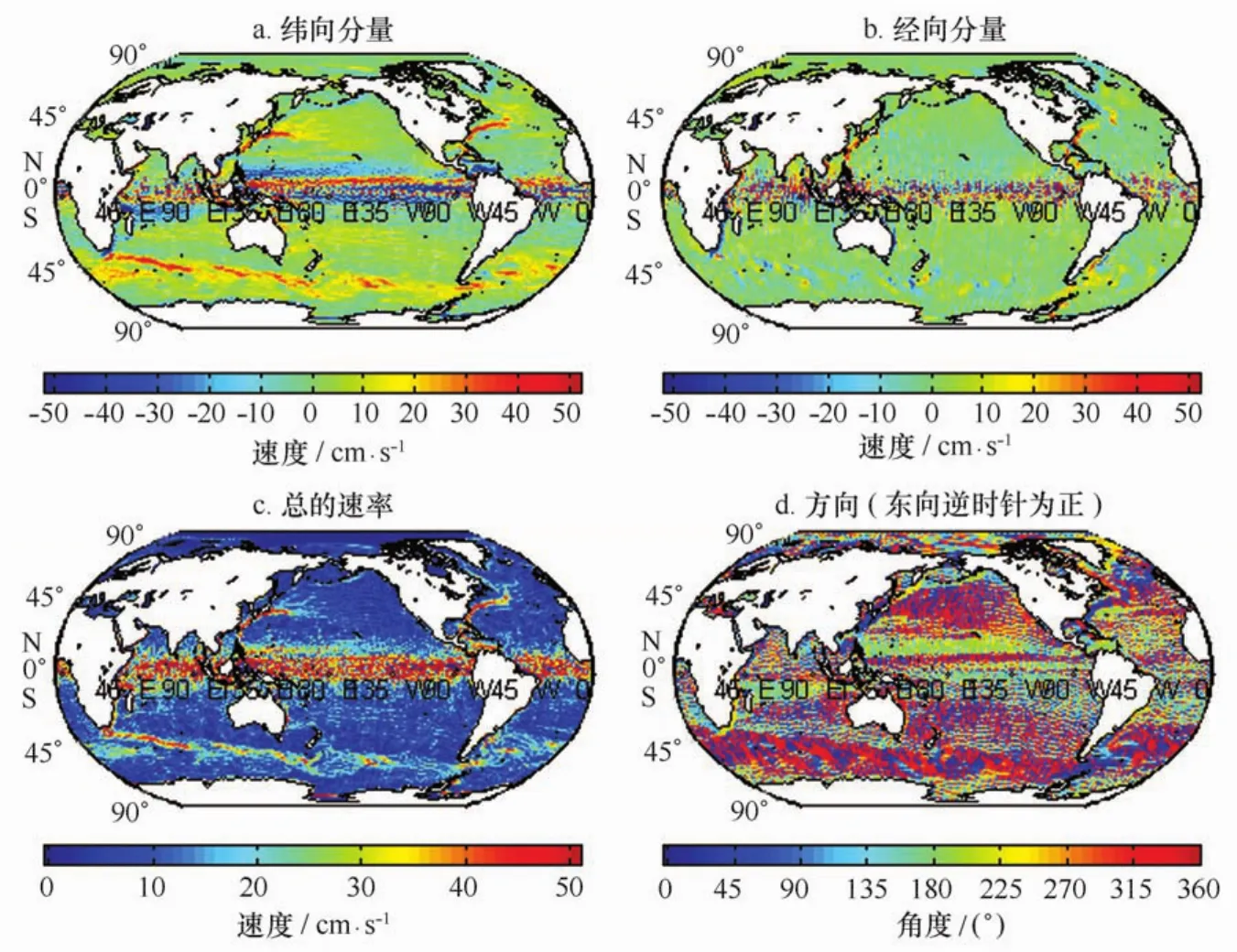
图3 GRACE得到的全球地转流Fig.3 Global ocean surface geostrophic currents predicted from GRACE

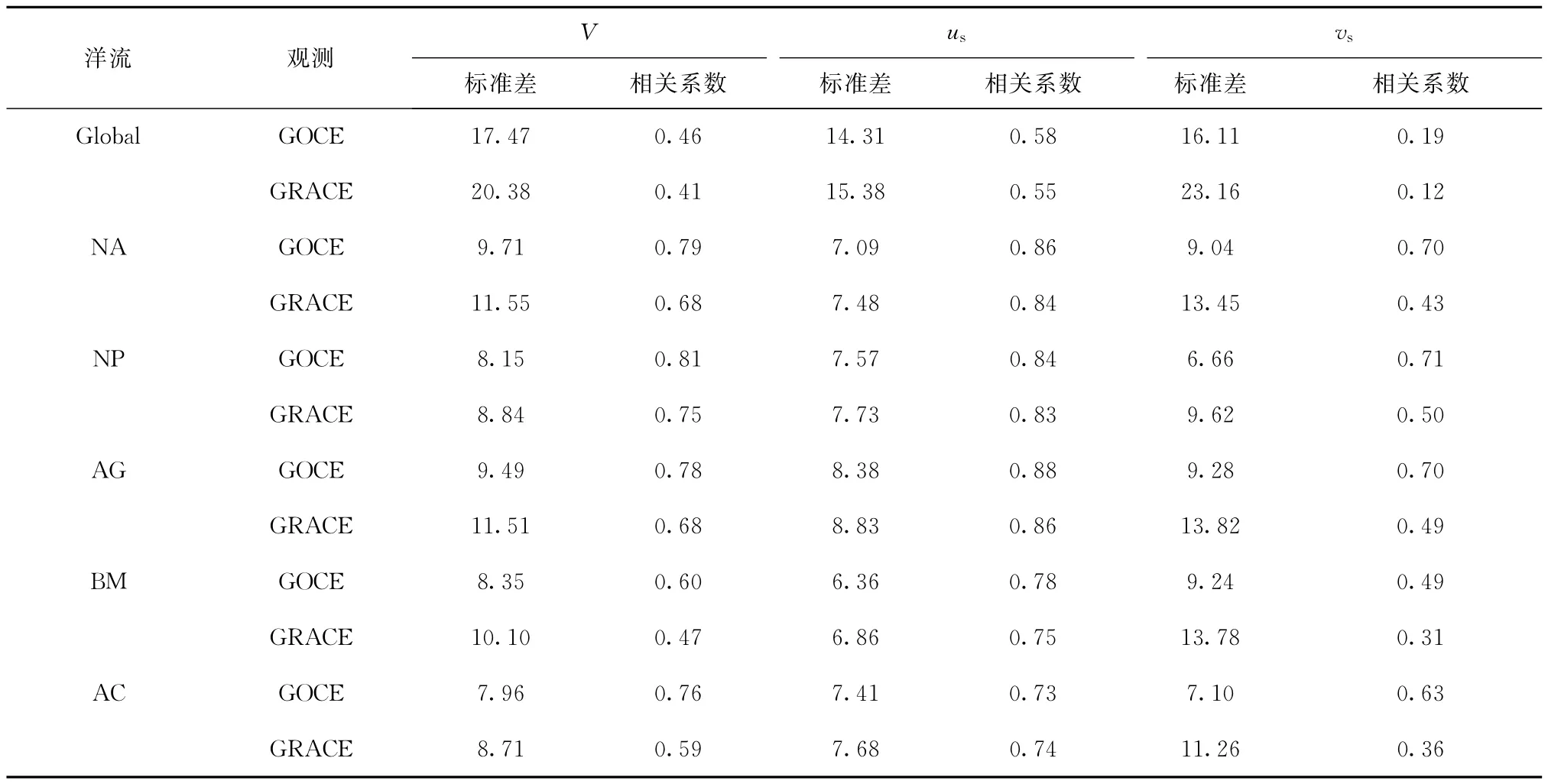
表1 GOCE和GRACE重力场模型确定的地转流与浮标实测结果的标准差和相关系数Tab.1 Statistics summarizing the differences between the GOCE and GRACE geostrophic currents and drifter observations（RMSand correlation coefficients）

图4表示大西洋上重要的洋流——墨西哥湾暖流，其中图4a表示基于GRACE重力场模型，4b表示基于GOCE重力场模型，4c表示CNES-CLS09的结果，4d实测浮标的结果。从图4中可以得出，基于GOCE得到的全球地转流与浮标实测结果符合的很好，能够反映出其局部细节的详细信息，而基于GRACE得到的全球地转流则含有太多的噪声信号。墨西哥湾暖流是世界大洋中最强大的暖流，也是最大的暖流。墨西哥湾暖流从30°N美国东海岸的哈特勒斯角附近偏向东北方向流，到达40°N，50°W处纽芬兰浅滩的东岸。将墨西哥湾暖流粗略地分为两个部分，第一部分，是在30°～36°N之间，墨西哥湾暖流作为一个狭窄的西边界流，沿着美国东海岸，在哈特勒斯角附近（点A）地转流速度达到最大。由GOCE得到的最大速度为58.32 cm／s，与浮标结果接近，而GRACE的结果仅为45.45 cm／s。在36°N处，墨西哥湾暖流远离海岸，开始向东流动，GOCE估计的地转流在70°W处（点B）为56.16 cm／s，而GRACE的结果为59.48 cm／s，实测浮标结果为44.52 cm／s。因此，GOCE的结果与实测浮标符合的更好。到了60° W的东边，墨西哥湾暖流流势减弱，这种转变能够在GOCE的结果中清晰的表现。第二部分，在38°N，44° W附近，墨西哥湾暖流遇到了Mann漩涡［21］，墨西哥湾暖流变为两个分支，向东为亚速尔群岛洋流［22］，向北为北大西洋暖流；Mann漩涡在其北侧面最为强大，在这方面，GOCE的结果与实测浮标数据更为接近，显示了GOCE能够获得更为精细的信息。子极环流的边界流也是北大西洋环流的一种重要的组成部分。在纽芬兰的东部（点C），实测浮标的结果表明拉布拉多洋流的速度为18.74 cm／s，GOCE的结果为22.89 cm／s，而GRACE结果为26.44 cm／s；在西格陵兰洋流的最南端（点D），实测浮标的结果表明拉布拉多洋流的速度为47.28 cm／s，GOCE的结果为28.29 cm／s，而GRACE结果为18.75 cm／s。图5表示了墨西哥湾暖流流速的矢量图，其中图5a表示基于GRACE重力场模型，图5b表示基于GOCE重力场模型。从图5中可以看出，GRACE的结果在20°～40°N，35°～70°W区域，误差偏大并且是杂乱无章的，不能反映出洋流的方向，而GOCE结果则没有出现这一现象。上述分析表明，GRACE重力场对中、小尺度的表层地转流细节的探测能力相对较弱，而基于GOCE重力场模型估计的全球海洋表面地转流能够反映出中、小尺度细节和特征。

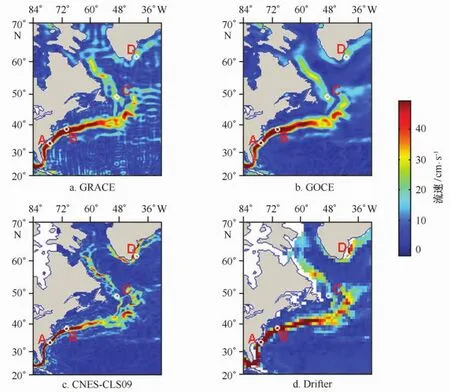
图4 GRACE、GOCE、CNES-CLS09和实测浮标估计墨西哥暖流Fig.4 Gulf Stream predicted from GRACE、GOCE、CNES-CLS09 and drifters

图5 墨西哥湾暖流流速的矢量图Fig.5 Gulf Stream predicted from GRACE and GOCE

3.2 误差分析

由误差传播定律可得，稳态海面地形的方差协方差阵为：

式中，Chh是平均海面高的方差协方差阵，CNN是大地水准面的方差协方差阵，ChN是两者的互协方差阵。由于大地水准面和平均海面高来源于两个不同的独立观测技术，因此两者之间的互协方差阵为0。公式（7）简化为：

将平均海平面高（h）可以展开为球谐系数的形式［23］，即：

式中，P˜′nm为完全规格化缔合勒让德函数P˜nm的一阶导数。因此，将重力场模型的位系数阶次的方差（δCnm，δSnm）和平均海平面高的球谐系数的方差（δCnHm，δSnHm），代入到式（10）和（11），可以计算得到基于ITG_Grace2010s和GOCE_TIM3的稳态海面地形和全球平均地转流的内符合精度。图6表示基于ITG_Grace2010s和GOCE_TIM3的稳态海面地形的精度，图7表示基于ITG_Grace2010s和GOCE_TIM3的全球平均地转流的精度。可以发现，在全球范围内，GOCE_TIM3的稳态海面地形和全球平均地转流的精度都比ITG_Grace2010s结果的精度有着很大的改善，其中ITG_Grace2010s的稳态海面地形的精度为21.6 cm，而GOCE_TIM3的结果则为7.45 cm，ITG_Grace2010s的全球平均地转流的精度为40.7 cm／s，而GOCE_TIM3的结果则为19.6 cm／s。

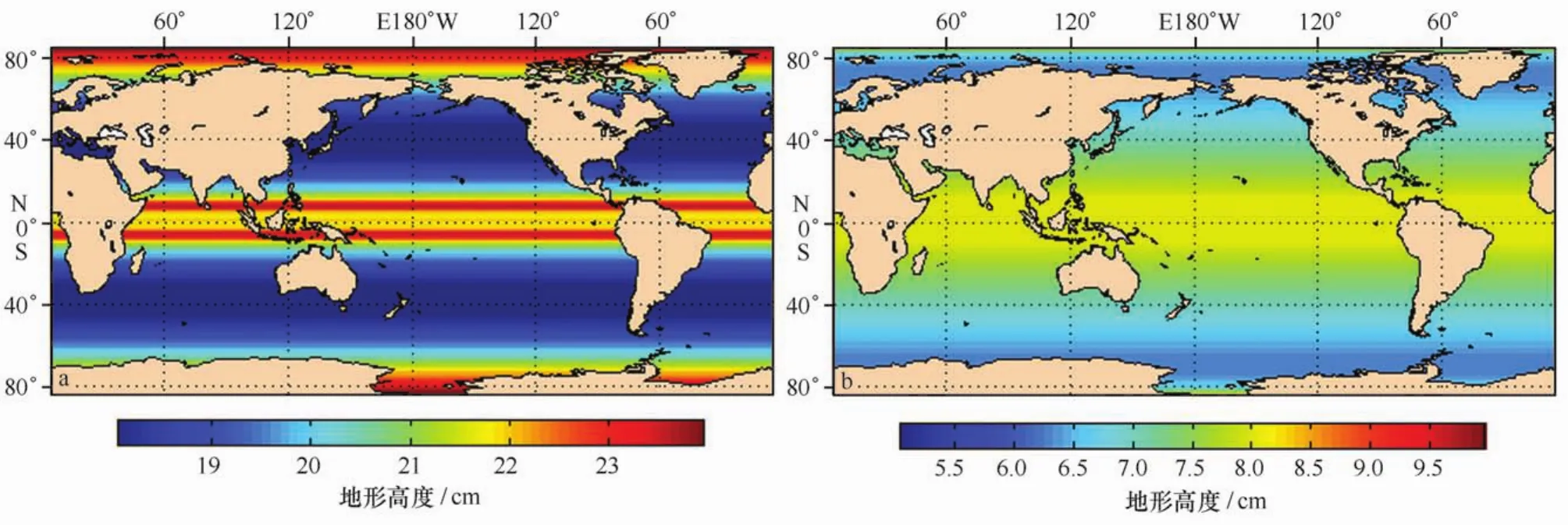
图6 基于ITG_Grace2010s（a）和GOCE_TIM3（b）的稳态海面地形的精度Fig.6 The accuracy of the MDT based on ITG_Grace2010s gravity model（a）and GOCE_TIM3 gravity model（b）

表2 不同重力场模型确定的地转流与浮标实测结果比较Tab.2 Global geostrophic currents estimated from different gravity field models in comparison with the drifters

图7 基于ITG_Grace2010s（a）和GOCE_TIM3（b）的全球平均地转流的精度Fig.7 The accuracy of the geostrophic currents based on ITG_Grace2010s MDT（a）and GOCE_TIM3 MDT（b）

进一步利用GOCE和基于不同时间跨度GRACE资料得到的重力场模型估计地转流结果与实测浮标结果进行比较，结果如表2所示。由表2中可以看出，随着融入更长时间的观测数据，基于GRACE重力场模型探测地转流的RMS逐渐减小，相关系数逐渐增大，可以明显的看出，GGM02S和GGM03S的分辨率相对较差，其RMS大于30 cm／s，相关系数也小于0.3。利用7年的观测数据得到的重力场模型ITG-Grace2010s，RMS达到了20.38 cm／s。而对于基于GOCE重力场模型探测的地转流的RMS，则在仅仅利用了18个月的观测数据时，其RMS就已经达到了17.47 cm／s，精度高于7年GRACE观测数据的结果，充分说明了GOCE确定全球地转流细节特征的突出能力。对于联合GRACE、CHAMP和GOCE系数得到的重力场模型GOCO03S确定的地转流，RMS与GOCE的结果相比，精度略有提高，但相关系数并没有明显改进，对于具体的原因，则有待进一步的研究。

4 结论

利用卫星重力数据和卫星测高数据获得了海面地形，进而确定全球海洋表面地转流，并与实测浮标数据进行比较分析。分析结果表明基于1～4年GRACE观测资料的模型不能很好估计全球地转流特征，近7年GRACE观测资料估计全球地转流仍含有较大的噪声，不能很好反应中小尺度地转流细节特征。而GOCE重力卫星确定的重力场模型具有更高的空间分辨率，能够确定高精度的全球海洋地转流，特别是中小尺度海洋表面地转流，如墨西哥湾暖流的细节信息，并且与实测浮标结果基本一致。利用7年的观测数据得到的重力场模型ITG-Grace2010s，RMS为20.38 cm／s，而基于18个月的GOCE重力场模型得到的地转流RMS为17.47 cm／s，精度高于7年GRACE观测数据的结果，充分说明了GOCE确定全球地转流细节特征的突出能力。并得到基于ITG_ Grace2010s和GOCE_TIM3的稳态海面地形和全球平均地转流的内符合精度，结果显示，在全球范围内，GOCE_TIM3的稳态海面地形和全球平均地转流的精度都比ITG_Grace2010s结果的精度有着很大的改善，其中ITG_Grace2010s的稳态海面地形的精度为21.6 cm，而GOCE_TIM3的结果则为7.45 cm，ITG_ Grace2010s的全球平均地转流的精度为40.7 cm／s，而GOCE_TIM3的结果则为19.6 cm／s。随着GOCE卫星的观测数据的积累，以及将来新的卫星重力计划，将进一步提供更高精度和更高分辨率的重力场模型，由此能够获得更加精细的全球表面地转流，对于监测和研究中小尺度表层地转流细节特征有着重要意义。

［1］黄瑞新.大洋环流：风生与热盐过程［M］.乐肯堂，史久新，译.北京：高等教育出版社，2012.

［2］Tapley B D，Chambers D P，Bettadpur S，et al.Large scale ocean circulation from the GRACE GGM01 Geoid［J］.Geophys Res Lett，2003，30（22）：2163－2166.

［3］Maximenko N，Niiler P，Centurioni L，et al.Mean dynamic topography of the ocean derived from satellite and drifting buoy data using three different techniques［J］.J Atmos Oceanic Technol，2009，26（9）：1910－1919.

［4］Jin S G，Chambers D P，Tapley B D.Hydrological and oceanic effects on polar motion from GRACE and models［J］.J Geophys Res，2010，115：B02403.

［5］张子占，陆洋，许厚泽.利用卫星测量技术和小波滤波方法探测表层地转流［J］.中国科学D辑：地球科学，2007，37（6）：753－760.

［6］Drinkwater M R，Floberghagen R，Haagmans R，et al.GOCE：ESA's first Earth Explorer core mission［J］.Space Science Reviews，2003，108（1／2）：419－432.

［7］Mayer Gürr，Eicker A，Kurtenbach E，et al.ITG-GRACE：global static and temporal gravity field models from GRACE data［M］／／System Earth via Geodetic-Geophysical Space Techniques.Berlin：Springer，2010：159－168.

［8］Pail R，Bruinsma S，Migliaccio F，et al.First GOCE gravity field models derived by three different approaches［J］.JGeod，2011，85（11）：819－843.

［9］Heiskanen W A，Mori H.Physical Geodesy［M］.W H Freemand and Company，San Francisco and London，1967.

［10］Stewart R H.Introduction to Physical Oceanography［M］.California，San Diego：Texas A＆M University，2008.

［11］Schaeffer P，Faugere Y，Legeais J F，et al.The CNES_CLS11 global mean sea surface computed from 16 years of satellite altimeter data［J］.Marine Geodesy，2012，35（supl）：3－19.

［12］Hughes C W，Bingham J R.An oceanographer's guide to GOCE and the geoid［J］.Ocean Sci Discuss，2008，4：15－29.

［13］Bingham R J，Haines K，Hughes C W.Calculating the ocean's mean dynamic topography from a mean sea surface and a geoid［J］.J Atmos Ocean Technol，2008，25：1808－1822.

［14］Albertella A，Rummel R.On the spectral consistency of the altimetric ocean and geoid surface，a one-dimensional example［J］.J Geod，2009，83：805－815.

［15］Jekeli C.Alternative methods to smooth the earth's gravity field［R］.Columbus：Ohio State University，1981.

［16］Wahr J，Molenaar M，Bryan F.Time-variability of the Earth's gravity field：Hydrological and oceanic effects and their possible detection using GRACE［J］.J Geophys Res，1998，103：32，205－30，229.

［17］Knauss J A.Introduction to physical oceanography［M］.2ed.New Jersey：Prentice-Hall，1997：309－310，

［18］Lagerloef GSE，Mitchum G T，Lukas R B，et al.Tropical Pacific near-surface currents estimated from altimeter，wind，and drifter data［J］.JGeophys Res，1999，104（C10）：23313－23326.

［19］Lumpkin R，Garraffo Z.Evaluating the decomposition of tropical Atlantic drifter observations［J］.J Atmos Oceanic Technol，2005，22：1403－1415.

［20］Lumpkin R，Pazos M.Measuring Surface currents with Surface Velocity Program Drifters：the Instrument，its Data，and some Recent Results［M］.Cambridge University Press，2007.

［21］Mann C R.The termination of the Gulf Stream and the beginning of the North Atlantic Current［J］.Deep Sea Research and Oceanographic Abstracts，1967，14（3）：337－359.

［22］Gould W J.Physical oceanography of the Azores front［J］.Prog Oceanog，1985，14：167－190.

［23］Albertella A，Savcenko R，Janjic T，et al.High resolution dynamic ocean topography in the Southern Ocean from GOCE［J］.Geophys J Int，2012，190：922－930.

Global ocean surface geostrophic currents estimated from satellite altimetry，GRACE and GOCE

Feng Guiping1，2，Jin Shuanggen2，Jose M.Sanchez Reales3

（1.Collegeof Marine Sciences，Shanghai University，Shanghai 201306，China；2.Shanghai Astronomical Observatory，Chinese A-cademy of Sciences，Shanghai 200030，China；3.University of Alicante，Alicante，Spain）

The satellite gravity mission GRACE（gravity recovery and climate experiment）has greatly improved the accuracy and resolution of the gravity field model of the earth，particularly in long-wave components.It can determine the characteristics of large scale global ocean surface currents combining satellite altimetry.In addition，the new generation GOCE（gravity field and steady-state ocean circulation explorer）mission was successfully launched in 2009 using gravity gradient measurements，which is very sensitive to the high-frequency part of the gravity field.Therefore，the GOCE is capable to determine the ocean surface currents with high spatial resolution.In this paper，the global surface geostrophic currents are determined from three models：（1）the gravity field model derived from 1 to 7 years of GRACE observations；（2）the gravity field model GO_CONS_GCF_2_TIM_R3 derived from one and half years of GOCE observations；（3）the mean sea surface topography model MSS_CNES_CLS_11 derived from satellite altimetry.It has shown that the gravity field model based on GOCE satellite gravity observations has a higher spatial resolution and can reflect more details and characteristics of the surface geostrophic currents with high accuracy and spatial resolution，e.g.，the medium and small-scale Mexico Gulf currents.Furthermore，the predictions are consistent with the in-situ drifters buoy data.However，the gravity model from 1 to 4 years of GRACE observations cannot predict global geostrophic currents accurately，and even the model from 7 years of GRACE observations is still less accurate than that from the one and half years of GOCE observations；the former one cannot reveal the details of current at the medium and small scales and has larger noises.

geostrophic currents；GOCE；GRACE；satellite altimetry

P731.21

A

0253-4193（2014）09-0045-11

冯贵平，金双根，Jose M.Sanchez Reales.利用卫星测高、GRACE和GOCE资料估计全球海洋表面地转流［J］.海洋学报，2014，36（9）：45—55，

10.3969／j.issn.0253-4193.2014.09.006

Feng Guiping，Jin Shuanggen，Jose M.Sanchez Reales.Global ocean surface geostrophic currents estimated from satellite altimetry，GRACE and GOCE［J］.Acta Oceanologica Sinica（in Chinese），2014，36（9）：45—55，doi：10.3969／j.issn.0253-4193.2014.09.006

2012-12-04；

2014-04-29。

国家自然科学基金项目——行星地球动力学扁率变化多卫星观测及其物理机制（11173050）；中科院重要方向项目——GPS，InSAR和卫星重力监测地表过程及其动力学（KJCX2－EW－T03）。

冯贵平（1988年—），男，湖北省宜昌市人，主要从事卫星大地测量与海洋遥感研究。E-mail：gpfeng＠shao.ac.cn

*通信作者：金双根，男，研究员，博士生导师，主要从事空间大地测量与遥感研究。E-mail：sgjin＠shao.ac.cn