A numerical study on dispersion of particles from the surface of a circular cylinder placed in a gas flow using discrete vortex method*
HUANG Yuan-dong (黄远东)
School of Environment and Architecture, University of Shanghai for Science and Technology, Shanghai 200093, China
College of Engineering, Kyung Hee University, Yongin 449-701, Korea, E-mail: huangyd@usst.edu.cn
HE Wen-rong (何文荣), WU Wen-quan (吴文权)
School of Environment and Architecture, University of Shanghai for Science and Technology, Shanghai 200093, China
KIM Chang-Nyung
College of Engineering, Kyung Hee University, Yongin 449-701, Korea
Industrial Liaison Research Institute, Kyung Hee University, Yongin 449-701, Korea
A numerical study on dispersion of particles from the surface of a circular cylinder placed in a gas flow using discrete vortex method*
HUANG Yuan-dong (黄远东)
School of Environment and Architecture, University of Shanghai for Science and Technology, Shanghai 200093, China
College of Engineering, Kyung Hee University, Yongin 449-701, Korea, E-mail: huangyd@usst.edu.cn
HE Wen-rong (何文荣), WU Wen-quan (吴文权)
School of Environment and Architecture, University of Shanghai for Science and Technology, Shanghai 200093, China
KIM Chang-Nyung
College of Engineering, Kyung Hee University, Yongin 449-701, Korea
Industrial Liaison Research Institute, Kyung Hee University, Yongin 449-701, Korea
(Received January 28, 2013, Revised May 27, 2013)
The dispersion of particles emitted from the surface of a circular cylinder placed in a gas flow at the Reynolds number of 200 000 is numerically investigated using the discrete vortex method coupled with a Lagrangian approach for solid particle tracking. The wake vortex patterns, the temporal-spatial distributions and trajectories as well as the dispersion functions for particles with various Stokes numbers (St) ranging from 0.001 to 1.0 are obtained. The numerical results reveal that: (1) Solid particles on the cylinder surface are picked up and then transported away from the cylinder by the wake vortex flow. (2) Solid particles emitted from the cylinder surface always follow the vortices in the cylinder wake, and the response of particles to wake vortices is directly related to their Stokes numbers (particles withSt=0.001, 0.0038, 0.01 can distribute both in the vortex core and around the vortex periphery, whereas those withSt=0.1, 1.0 can not enter the vortex core and congregate mainly around the vortex periphery). (3) The particles move in rolling state in the wake region, and the dispersion intensity of particles in the lateral direction decreases remarkably as the Stokes number of particles is increased from 0.001 to 1.0.
particle dispersion, circular cylinder, gas flow, wake vortex, discrete vortex method (DVM)
Introduction
Particle dispersion in gas flows over a circular cylinder is very common in man-made and natural environments. Because gas flows past a circular cylinder (bluff body) at high Reynolds number are characteri-zed by the evolution of wake vortices, understanding the effect of wake vortices on particle dispersion in the wake of a circular cylinder is crucial for predicting spatial and temporal distributions of particles and for analyzing the erosion of cylinder surface. The numerical studies of particle dispersion in plane mixing layers[1-3], planar jets[4,5], and wake gas flows behind a flat plate[6]and over a backward-facing step[7]have been made extensively, and it was found that the large organized vortex structures have a dominate effect on the dispersion of particles over a range of Stokes numbers. Recently, a few numerical studies have been conducted to investigate particle-laden gas flows past single and multiple circular cylinders[8-12], and it was revealed that the particle dispersion pattern depends strongly on wake vortices and particle’s Stokes number.
Particle emissions from bluff body surfaces occur widely in engineering practice and in natural environment. For example, particulate matters are released from a bluff body surface during its erosion process in a flow. Also, solid particles already deposited on a bluff body may be picked up again by flows past the bluff body. In the above-mentioned studies[8-12], however, the solid particles were all from the free-stream and the dispersion of particles from the surface of a circular cylinder was not simulated. On the other hand, the dispersion of very small sized particles was not considered in the above-mentioned investigations (i.e., the Brownian force and the Cunningham correction factor to Stokes’ drag law were not taken into account in previous studies).
The objective of the present work is to investigate numerically the effect of wake vortices on dispersion of different sized particles from the surface of a circular cylinder placed in a gas flow at high Reynolds number. To this end, we study the two-dimensional gas flows past a circular cylinder at the Reynolds number of 200 000. In the numerical procedure, the discrete vortex method with a diffusion velocity model for diffusion of vorticity due to fluid viscosity, which can capture the essential features (such as the formation, development and decay of wake vortices) of the unsteady gas flows, is used to evaluate the unsteady gas flow fields, a Lagrangian approach based on one-way coupling is adopted to track individual solid particles released from the cylinder surface, and a dispersion function is applied to represent the lateral dispersion scale of particles. In the simulations, the changes in particle distribution patterns, particle trajectories and particle dispersion intensity with the Stokes number are all examined.
1. Basic equations and numerical method
1.1Unsteady gas flow field
1.1.1 Governing equations for gas
We use the discrete vortex method (DVM)[9,13-15]to evaluate the unsteady gas flow fields numerically.
For a two-dimensional, viscous incompressible flow past a circular cylinder at high Reynolds number, the governing equations in the vorticity-stream function form are given as

wheretis the time,νthe kinematic viscosity,ωthe vorticity, andψthe stream function.
The fluid vorticityωis expressed by

whereuandvare the velocity components in thex- andy-directions, respectively.
The stream functionψis related to the velocity components through

The discrete vortex method represents the continuous vorticity field as the sum of a large numberNof vortex blobs

wherer=(x,y),Γiis the strength of theith vortex blob at positionri=(xi,yi), andKσ(ε) is the cutoff function given as

whereσis the core radius of the vortex blob.
When the vorticity field is discretized into a set ofNvortex blobs, the velocity field is constructed from the vortex blobs by the following equations derived from the Biot-Savart Law.

whereu∞andv∞are the free-stream velocity components in thex- andy-directions, respectively

Fig.1 Distribution of nascent vortex blobs along the circular cylinder surface[9]
1.1.2 Generation and shedding of discrete vortex blobs from the cylinder surface
A circular cylinder surface is represented byMcontrol points, which are placed at a very small distanceδfrom the surface. At each control point, a nascent vortex blob is created at each time step (as depicted in Fig.1) to satisfy the zero normal velocity condition.
The separation points are calculated by using the boundary layer theories. Once the separation points are determined, the nascent vortex blobs at and downstream of the separation points are shed into the wake.
1.1.3 Diffusion of vorticity due to viscosity
The diffusion of vorticity due to fluid viscosity is modeled by a diffusion velocity method presented by Ogami and Akamatsu[9]. In this method, the transport equation for a scalar functionF(x,y,t) moving with a fluid velocityV(x,y,t)=[u(x,y,t),v(x,y,t)]in the (x,y)-plane is given by
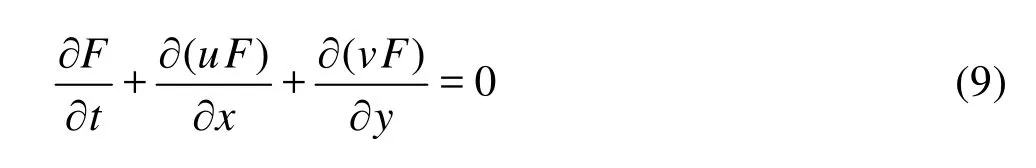
The vorticity transport Eq.(1) may be rewritten as

Through comparing Eqs.(9) and (10), the vorticityωcan be considered as moving with a total velocity of (V+Vd), whereVis the usual convective velocity. Hence the effect of viscosity is to add a diffusion velocity componentVd=(ud,vd)to the motion of each vortex blob, whereudandvdare given by

By substituting Eq.(5) into Eq.(11), the diffusion velocity (ud,vd) induced at position (x,y) and timetcan be expressed as

Therefore, in the diffusion velocity method, each vortex blob is transported both by the convection velocity (u,v) obtained from Eqs.(7) and (8) and by the diffusion velocity (ud,vd) calculated from Eqs.(12) and (13), and its strength is kept invariant along its trajectory according to Eq.(10).
After getting the convection and diffusion velocities of each vortex blob, its position can be determined by integrating the following equation

whereri=(xi,yi) is the position of theith vortex blob.
When the position and strength of each vortex blob are known att=t, the flow att=t+Δt(Δtis the size of the time step) can be obtained, because the gas velocity is calculated from Eqs.(7) and (8), and the position of vortex blob is obtained from Eq.(14).
1.2Lagrangian equation of motion for a particle
We adopt a Lagrangian approach based on oneway coupling between the continuous gas phase and dispersed particles to simulate the particle motion in unsteady gas flow fields. In this study, the free-stream is clean and the particles are only released from the cylinder surface, thus the impact of particles on airflow as well as the inter-particle collisions can be ignored due to extremely small particle concentrations in the flow field. In the present simulation, the forces acting on a particle are the drag, virtual mass, pressure gradient, Saffman’s lift, and Brownian motion forces (here the Magnus and Basset forces are omitted). And thus the Lagrangian equation of motion for a spherical particle we used is

wherepρandρare the particle and fluid density, respectively,dpis the particle diameter,μis the dynamic viscosity of the fluid,V=(u,v) andVp=(up,vp) are the instantaneous velocity of the fluid and the particle, respectively,fis the modification factor for the Stokes drag coefficient,φ(t) is a Brownian force per unit mass,iandjare the unit vectors inx- andy-directions, respectively,tis the time, d/ dtis the temporal derivative along the discrete particle trajectory and D/Dtis the temporal derivative along the fluid motion. d/dtand D/Dtcan be written as
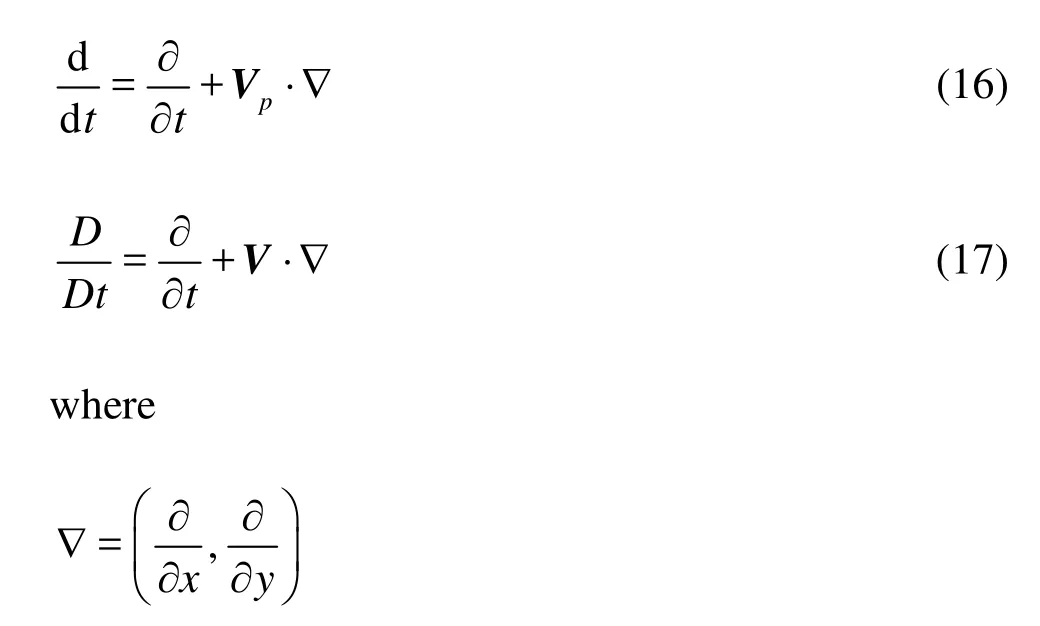
The terms on the right-hand side of Eq.(15) represent, respectively, the drag, virtual mass, pressure gradient, saffman’s lift, and Brownian motion forces. The particle Reynolds number is defined by

fis related to the particle Reynolds number and is given below
Cin Eq.(19) is the Cunningham correction factor to Stokes’ drag law, which can be calculated from

whereλis the molecular mean free path of the gas and is given by

For small particles the effect of Brownian motion becomes significant[16,17]. To take into account such effects in the simulation of particle motion the Brownian force is modeled as a Gaussian white noise random process, and the amplitudes of the Brownian force components at every time step are evaluated from


Fig.2 Coordinate system for the numerical simulations
Equation (15) can be further simplified to give


Fig.3 Distributions of particles withSt=0.001 and discrete vortex blobs at different time instants (the solid circles represent particles and hollow circles vortex blobs)

The Stokes number (St) is used widely by various researchers to study particle dispersion in flowing gases, which is defined as the ratio of the response time of the particle to the time scale of the fluid. Let the circular cylinder diameterDbe a characteristic lengthL, the upstream approach velocityV∞be a characteristic velocityU, andT=L/U=D/V∞be the characteristic time. If the time scale of the mean flow,L/U, is used, the Stokes number can be evaluated as

According to the definition of velocity, we have

whererp(t) is the location of the particle at timet.
We first solve the Eq.(26) to get the particle velocity, and then integrate the Eq.(28) to determine the particle position in the unsteady flow field.
1.3Numerical procedure
In the numerical simulation, the unsteady gas flow field is first evaluated by using the discrete vortex method, based on the obtained unsteady gas velocity field, the Lagrangian equations of motion for particles are then solved to track the individual solid particles.
2. Numerical results and its analysis
2.1Calculating conditions
We use the above numerical method to simulate

Fig.4 Distributions of particles withSt=1.0 and discrete vortex blobs at five different time instants (the small solid circles represent particles and small hollow circles vortex blobs)

Fig.5 Distributions of particles and discrete vortex blobs at timet=20 (the small solid circles represent particles and small hollow circles vortex blobs)
the particle dispersion in the wake of gas flows over a circular cylinder at high Reynolds number. Figure 2 shows the coordinate system of the numerical simulations. The origin is taken at the center of the fixed cylinder with a non-dimensional diameter of 1.0. Thex- axis is parallel to the undisturbed stream and the flow plane is perpendicular to the gravity. The flow is from left to right, at timet=0 the flow is started with constant non-dimensional velocity of magnitude 1.0 in thex-direction. Thus the gas velocity at position (-∞,0) is (1,0). The kinematic viscosity of the fluid is 1.5×10–5m2/s and the absolute temperature of the fluid is 293 K. The Reynolds number based on the cylinder diameter and the gas velocity upstream of the cylinderV∞is 200 000.pρandρare 2 650 kg/m3and 1.2 kg/m3, respectively. Six different particles for the Stokes numbers,St, of 0.001, 0.0038, 0.01, 0.061, 0.1 and 1.0 are calculated (since PM10 and PM2.5 levels are widely used in assessment of atmospheric quality in environmental science, we also evaluate in this study the dispersion of particles withdp=10μ m (St=0.061) and 2.5μ m(St=0.0038)).
The circular cylinder surface is represented by the 103 control points with fixed locations, and 103 nascent vortex blobs are created at each time step on the cylinder surface. The maximum number of vortex blobs is 20 000 (i.e., nearly two hundred times the number of the nascent vortex blobs) in the simulation (in a previous study[9], the maximum number of vortex blobs is twenty times that of the nascent vortex blobs). The time step size Δtof the simulation of fluid flow is set to be 0.02, and the total number of time steps is 1 000 (i.e., the simulation runs to timet=20).
At each time step, as the simulation for the gasphase has been completed, 50 spherical particles of monosize distribution are released randomly from the cylinder surface into the gas flow field (the initial position of each particle is determined by using random numbers and the initial velocity of each particle is set to be zero).
In order to obtain the particle trajectories, we track 50 spherical particles for each of the four different particles for the Stokes numbers 0.001, 0.01, 0.1 and 1.0. These particles tracked are evenly distributed along the cylinder surface and released at timet=0 into the gas flow field.
In order to quantitatively study the dispersionscales of particles with different Stokes numbers, the dispersion function in theydirection is used here. The dispersion function is defined as[9,14]

whereNpis the total number of particles in the cal-
culating region at timet,Yi(t) is the displacement of theith particle in they- direction from timet-Δttot,Ym(t) is the mean value of particle displacement in theydirection from timet-Δttot.
2.2Numerical results
Figure 3 shows the five instantaneous images of the discrete vortex blob pattern and of the distribution of particles with very small Stokes number 0.001. The vortex blob patterns depicted in Fig.3 illustrate that the vortex blobs shed from the cylinder form clusters in the wake region. Due to the flow separation, vortices occur downstream of the separation points on the cylinder surface. Figure 3 reveals clearly that the particles on the cylinder surface are picked up and then transported away from the cylinder by the wake vortex flow. Figure 3 also reveals that in the wake region the particles from the cylinder surface always follow the wake vortices (or the clusters of discrete vortex blobs) and are distributed both in the vortex core and around the vortex periphery.
Figure 4 shows the five instantaneous images of the discrete vortex blob pattern and of the distribution of particles with intermediate stokes number 1.0. From this figure, it can be observed that in the wake region the particles withSt=1.0 also follow the wake vortices. But unlike the particles with very small Stokes number 0.001, the particles withSt=1.0 can not enter the vortex core and they distribute only around the vortex periphery.
In order to examine the effects of wake vortices on distribution of particles with various Stokes numbers, at timet=20 the discrete vortex blob pattern and the particle distributions, respectively, for Stokes numbers 0.001, 0.0038, 0.01, 0.061, 0.1 and 1.0 are shown in Fig.5. This figure indicates clearly that the dispersion of particles in the circular cylinder wake is governed by the Stokes number and the structure of wake vortices.
Due to the very small inertia effects, the particles with very small Stokes numbers 0.001, 0.0038 and 0.01 can distribute both in the vortex core and around the vortex periphery as shown in Figs.5(a) through 5(c).
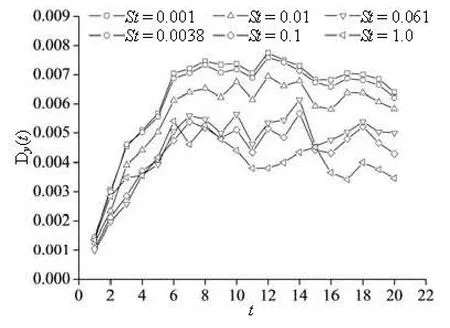
Fig.6 Time series of dispersion function of particles with different Stokes numbers

Fig.7 Trajectories of particles with various Stokes numbers (the particles are released into the gas flow field at timet=0)
Due to the strong centrifugal force acting on the particle by the vortices, the particles with intermediateStokes numbers (St=0.1, 1.0) cannot enter the vortex core and congregate mainly around the vortex periphery or near the outer boundaries for the clusters of vortex blobs as depicted in Figs.5(e) and 5(f).
For particles with the Stokes numbers ranging from 0.01 to 1.0, Figs.5(c) through 5(f) shows clearly that the zones around the vortex cores, where few particles exist, are expanded as the Stokes number is increased. This is because the centrifugal force acting on a particle by the wake vortices increases with the Stokes number.
Figure 6 shows the time series of dispersion function for particles with different Stokes numbers (St=0.001, 0.0038, 0.01, 0.061, 0.1, 1.0). It is evident from this figure that the particle’s dispersion intensity in the lateral direction decreases significantly asStis increased from 0.001 to 1.0 (the dispersion intensity of particles withSt=0.001 is nearly twice that of particles withSt=1.0).
The trajectories of particles with four different stokes numbers (St=0.001, 0.01, 0.1, 1.0) are shown in Fig.7, which illustrates clearly that the particles rollingly move in the wake region, and that the particle fluctuations in the lateral direction increase remarkably with the decrease of particle’s Stokes number.
3. Conclusions
The dispersion of particles from the surface of a circular cylinder placed in a gas flow at Reynolds number of 200 000 has been numerically studied using the discrete vortex method coupled with a diffusion velocity model and Lagrangian solid particle tracking. The vortex patterns, the distributions and time series of dispersion function for particles with the Stokes numbers 0.001, 0.0038, 0.01, 0.061, 0.1 and 1.0, and the trajectories of particles with Stokes numbers 0.001, 0.01, 0.1 and 1.0 are obtained. The numerical results show that the dispersion of particles released from a cylinder surface is governed by the particle’s Stokes number and the structure of wake vortices: (1) Particles on the cylinder surface are picked up and then transported away from the cylinder by the wake vortex flow. (2) Particles from the cylinder surface always follow the wake vortices in the wake region, and the particles with very small Stokes numbers (such asSt=0.001, 0.0038, 0.01) can distribute both in the vortex core and around the vortex periphery, whereas those with intermediate Stokes numbers (such asSt= 0.1, 1.0) can not enter the vortex core and congregate mainly around the vortex periphery. (3) The zones around the vortex cores, where few particles exist, are expanded as the Stokes number is increased from 0.01 to 1.0. (4) The particles move in rolling state in the wake region, and the particle’s dispersion intensity in the lateral direction decreases remarkably asStis increased from 0.001 to 1.0 (the dispersion intensity of particles withSt=0.001 is nearly twice that of particles withSt=1.0).
This work is helpful for environmental researchers to analyze and predict the spatial and temporal distributions of particulate matters released from the surface of a bluff body.
It should be noted that this study is restricted to discussion in two-dimensional flows and further investigations are still needed to simulate particle dispersion in three-dimensional airflows past a circular cylinder.
[1] YANG X., RIELLY C. and LI L. et al. Modelling of heavy and buoyant particle dispersion in a two-dimensional turbulent mixing layer[J].Powder Technology,2007, 178(3): 151-165.
[2] NARAYANAN C., LAKAHEL D. and YADIGAROGLU G. Linear stability analysis of particle-laden mixing layers using lagrangian particle tracking[J].Powder Technology,2002, 125(2-3): 122-130.
[3] JONES W. P., LYRA S. and MARQUIS A. J. Large eddy simulation of a droplet laden turbulent mixing layer[J].International Journal of Heat and Mass Transfer,2010, 31(1): 93-100.
[4] FAN Q. L., WANG X. L. and ZHANG H. Q. et al. Large eddy simulation of a horizontal particle-laden turbulent planar jet[J].Computational Mechanics,2001, 27(2): 128-137.
[5] ALMEIDA T. G., JABERI F. A. Direct numerical simulations of a planar jet laden with evaporating droplets[J].International Journal of Heat and Mass Transfer,2006, 49(13-14): 2113-2123.
[6] UCHIYAMA T., YAGAMI H. Numerical analysis of gas-particle two-phase wake flow by vortex method[J].Powder Technology,2005, 149(2-3): 112-120.
[7] YU K. F., LAU K. S. and CHAN C. K. Large eddy simulation of particle-laden turbulent flow over a backward-facing step[J].Communications in Nonlinear Science and Numerical Simulation,2004, 9: 251-262.
[8] CHEN B., WANG C. and WANG Z. et al. Investigation of gas-solid two-phase flow across circular cylinders with discrete vortex method[J].Applied Thermal Engineering,2009, 29(8-9): 1457-1466.
[9] HUANG Y., WU W. and ZHANG H. Numerical study of particle dispersion in the wake of gas-particle flows past a circular cylinder using discrete vortex method[J].Powder Technology,2006, 162(1): 73-81.
[10] ZHOU H., MO G. and CEN K. Numerical investigation of dispersed gas-solid two-phase flow around a circular cylinder using lattice Boltzmann method[J].Computers and Fluids,2010, 52: 130-138.
[11] HUANG Yuan-dong, ZHANG Hong-wu and WU Wenquan. Numerical study of particle distribution in the wake of gas-particle two-phase flows past a circular cylinder at high Reynolds number[J].Journal of Hydrodynamics, Ser. B,2005, 17(3): 283-288.
[12] LIU L., JI F. and FAN J. et al. Direct numerical simulation of particle dispersion in the flow around a circular cylinder[J].Journal of Thermal Science,2004,13(4): 344-349.
[13] RICHMOND-BRYANT J., FLYNN M. R. Applying the discrete vortex method in environmental fluid mechanics: A study of the time-averaged near wake behind a circular cylinder[J].Environmental Fluid Mechanics,2004, 4(4): 455-463.
[14] HUANG Y. Numerical study of particle dispersion in the wake of two tandem square cylinders using discrete vortex method[J].Particulate Science and Technology,2011, 29(6): 526-540.
[15] UCHIYAMA T., NARUSE M. H. A Numerical method for gas-solid two-phase free turbulent flow using a vortex method[J].Powder Technology,2001, 119(2-3): 206-214.
[16] JAFARI S., SALMANZADEH M. and RAHNAMA M. et al. Investigation of particle dispersion and deposition in a channel with a square cylinder obstruction using the lattice Boltzmann method[J].Journal of Aerosol Science,2010 41(2): 198-206.
[17] AFROUZI H. H., FARHADI M. and MEHRIZI A. A. Numerical simulation of microparticles transport in a concentric annulus by lattice Boltzmann method[J].Advanced Powder Technology,2013, 24(3): 575-584.
10.1016/S1001-6058(14)60043-3
* Project supported by the Innovation Program of Shanghai Municipal Education Commission (Grant No. 10ZZ95), the Leading Academic Discipline Project of Shanghai Municipal Education Commission (Grant No. J50502).
Biography: HUANG Yuan-dong (1965-), Male, Ph. D.,
Professor
Corresponging author: KIM Chang-Nyung,
E-mail: cnkim@khu.ac.kr
- 水动力学研究与进展 B辑的其它文章
- Effect of bank slope on the flow patterns in river intakes*
- Influence of artificial ecological floating beds on river hydraulic characteristics*
- Numerical investigation of flow through vegetated multi-stage compound channel*
- Responses of thermal structure and vertical dynamic structure of South China Sea to Typhoon Chanchu*
- Effect of vegetated-banks on local scour around a wing-wall abutment with circular edges*
- URANS simulations of ship motion responses in long-crest irregular waves*

