基于IFOA-RBF算法的混凝土抗压强度预测
徐富强陶有田,2,3
(1 巢湖学院数学系,安徽 巢湖 238000)
(2 中国科学技术大学数学科学学院博士后流动站,安徽 合肥 230026)
(3 安徽富煌钢构有限公司博士后工作站,安徽 巢湖 238076)
基于IFOA-RBF算法的混凝土抗压强度预测
徐富强1陶有田1,2,3
(1 巢湖学院数学系,安徽 巢湖 238000)
(2 中国科学技术大学数学科学学院博士后流动站,安徽 合肥 230026)
(3 安徽富煌钢构有限公司博士后工作站,安徽 巢湖 238076)
为了提高混凝土抗压强度预测精度,利用改进果蝇优化算法(IFOA)优化RBF神经网络的参数Spread值,建立IFOA-RBF预测模型用于混凝土抗压强度预测。模型以UCI数据库中的Concrete Compressive Strength数据集为例,以每立方混凝土中的水泥、高炉矿渣粉、粉煤灰、水、减水剂、粗集料和细集料的含量以及置放天数为网络输入,混凝土抗压强度值作为网络输出,进行仿真测试,并将结果与参考文献中的其它方法比较。结果表明:优化后的RBF网络既体现了广泛映射能力,又明显地提高了网络的泛化能力。验证了IFOA-RBF模型在混凝土抗压强度预测中的有效性。
果蝇优化算法;RBF神经网络;参数优化;混凝土抗压强度
1 引言
混凝土抗压强度是否符合设计规定是工程质量控制中的重要研究内容之一,其正确预测,对提高施工质量、加快工程进度等方面起到非常重要的作用。目前,普通的混凝土抗压强度值描述和预测,一般是以灰水比为主要因素的线性函数。而对于高掺量的粉煤灰和矿渣混凝土,由于掺量成分的不同和增加,使影响因素具有更为复杂的交互作用,表现为某种特定的非线性规律[1]。人工神经网络是目前已经确定的解决此类高度复杂的非线性函数的有效方法之一,其中径向基神经网络(RBF神经网络)具有可调参数少、结构简单、输出与初始权值无关、学习收敛速度快等特点,能够逼近任意非线性函数,成为人工神经网络中应用较多的网络之一。在设计RBF神经网络时,合理选择参数SPREAD值很重要,往往都是通过选取不同的SPREAD值带入网络不断尝试,获得当前最佳实验结果。这就具有一定的不确定性和主观性,不易得到最优模型。本文提出利用改进的果蝇优化算法(IFOA)优化RBF神经网络用于混凝土抗压强度预测,利用Concrete Compressive Strength数据集设计仿真实验,并与参考文献其他算法对比研究,从而说明该方法的有效性。
2 果蝇优化算法(FOA)简介
果蝇优化算法[2](Fruit Fly Optimization Algorithm,简称FOA)是由台湾学者潘文超于2011年提出的最新演化式计算技术。FOA算法是一种基于果蝇觅食行为推演出寻求全局优化的群体智能的新方法。由于果蝇本身在感官和知觉上优于其它物种,尤其在视觉和嗅觉上。果蝇的嗅觉器官能很好的搜集空气中的各种气味,甚至能嗅到40公里以外的食物源。在飞近食物后,利用敏锐的视觉发现食物或同伴聚集的位置,并往该方向飞去。[3]
该算法的基本步骤:
步骤一,随机初始果蝇群体的位置(X-axis,Y-axis)。
步骤二,赋予果蝇个体利用嗅觉搜寻食物的随机方向(Random Value)与位置(X,Y)。
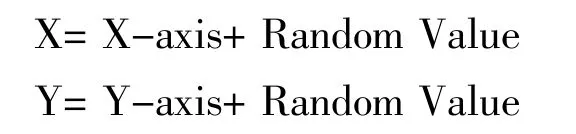
步骤三,计算果蝇个体与原点的距离(Dist),并计算味道浓度判定值(S),此值为距离的倒数。
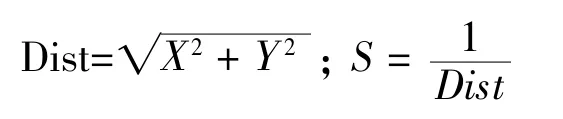
步骤四,将味道浓度判定值(S)代入味道浓度判定函数(Function),求出该果蝇个体所在位置的味道浓度(Smell)。
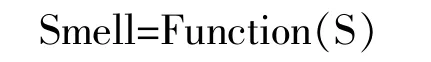
步骤五,重复步骤二至步骤四,计算果蝇群体的每个果蝇个体的味道浓度,并找出味道浓度最高(低)的果蝇。
步骤六,保存最优果蝇的味道浓度值与位置(X,Y)。此时,群体往该位置飞去。
步骤七,进入迭代寻优,重复执行步骤二至步骤五,并判断味道浓度值是否优于前一次迭代的味道浓度值,若是,执行步骤六,否则调至步骤二。直至满足最大迭代次数,算法结束,输出结果。
虽然FOA提出较晚,算法还不成熟,国内外研究成果并不显著,但FOA已体现了其优越的寻优性能,可成功应用到多个领域[4-7]。
3 径向基神经网络(RBF)简介
径向基神经网络又称RBF神经网络,属于前向型神经网络。网络的结构与多层前向网络类似,是一个只有一个隐藏层的三层前向网络。第一层为输入层,有信号节点组成;第二层为隐藏层,该层节点视问题而定,该层神经元的转化函数即径向基函数是局部响应的高斯函数;第三层为输出层。RBF神经网络结构见图1。
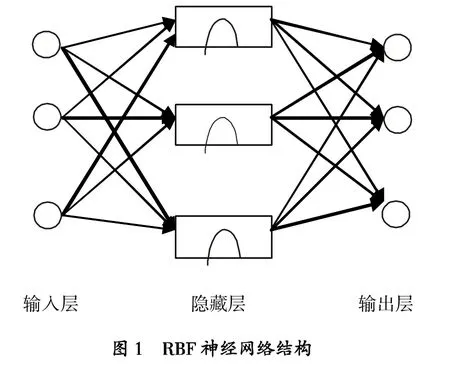
RBF网络就是用径向基作为隐单元的 “基”构成隐藏层,对输入矢量进行变换,将低维模式的输入数据变换到高维空间内,这样就将低维空间内线性不可分的问题转化到高维空间内线性可分,问题得以解决。
RBF神经网络学习方法有多种,本文利用自组织选取中心学习法,该学习过程分两步:第一步是自组织学习阶段,求解隐藏层基函数的中心和方差;第二步求解隐藏层到输出层间的权值。在训练过程中,隐藏层神经元数量的确定是一个关键问题,基本原理是从O个神经元开始训练,通过检查输出误差是否满足条件,否则自动增加神经元,每次循环使用,使网络生成的最大误差对应的输入矢量作为权值向量,产生一个新的神经元,然后检查新网络的误差,重复此过程,直到误差达到要求或达到最大隐藏层神经元数为止。RBF神经网络具有结构简单、自适应、输出与初始权值无关等特点,且其学习收敛速度快,能够逼近任意非线性函数[8]。
4 IFOA-RBF算法实现
参数SPREAD为径向基函数的扩展速度。在构建好RBF神经网络后,网络学习训练时,SPREAD值的大小直接影响网络的拟合 (预测)精度,合理选择SPREAD值非常重要。SPREAD值越大,能使径向基神经元对输入矢量所覆盖的空间都产生响应,但也不需要所有径向基神经元都产生响应,只要部分响应就足够了,而且SPREAD值太大也会导致计算上的困难。在网络设计时往往都是选取不同的SPREAD值进行尝试,这种方式具有一定的主观性和不确定性,不易得到最优模型[8]。
为了寻求最优模型,本文将RBF神经网络引入FOA算法的迭代寻优过程中,并对FOA部分步骤进行改进 (Improvement of Fruit Fly Optimization Algorithm,IFOA),称为 IFOA-RBF算法,该算法就是将味道浓度判定值S直接作为SPREAD值,将网络预测误差绝对值和作为味道浓度判定函数Smell值。IFOA相比基本FOA,对初始果蝇群体位置的方式做了改进,保证了种群的多样性,并对味道浓度判定值S做了改进,使更适应RBF网络。具体改进与实现步骤如下:


5 基于IFOA-RBF算法的混凝土抗压强度预测模型

本文的实验研究采用了 UCI的Concrete Compressive Strength数据集[9]。数据集中包含了1030×9组数据,其中前7列为每立方混凝土中各配料的含量,包括水泥、高炉矿渣粉、粉煤灰、水、减水剂、粗集料和细集料,第 8列为混凝土置放天数,第9列为混凝土抗压强度 (单位:MPa)。本实验以前8列数据作为RBF网络输入,第9列数据为网络输出。由于这9列数据代表的物理意义不同,为了避免输入和输出向量的不同纲量大小对网络训练的影响,需要对输入、输出向量分别进行归一化处理,这里用MATLAB自带的mapminmax函数完成。
对1030组实验数据,为了防止RBF网络过度拟合,影响网络推广能力,本文随机选取950组作为训练输入,50组作为仿真预测,剩余30组用于最佳RBF网络的预测。IFOA-RBF算法就是计算每次50组仿真预测误差,找到使网络误差绝对值和最小时的迭代次数及对应的Smell值和SPREAD值,从而找到当前条件下最佳SPREAD值。并利用最佳SPREAD值建立RBF网络,用于混凝土抗压强度预测。带入剩余30组输入数据,获得预测输出,并与实测值比较,评价模型的优劣。


设定果蝇搜寻范围为 [0.1,10],移动步长为0.1,种群规模sizepop=50,迭代次数maxgen=20。RBF神经网络创建命令为 newrbe(pp′,tt′,SPREAD),网络其它参数默认。算法运行一次得到最优SPREAD值为8.2707,实验运行结果见图2-图4。图2为最优果蝇个体适应度值变化曲线,图3为30组样本的预测值与期望值对比,图4为预测误差曲线图(实测值-预测值),预测的相对误差平均值为4.17%。

相比文献[12]方法,都是针对同一UCI数据集,采用1020组训练样本、10组预测样本,而本文采用950组训练样本,30组作为预测样本,实验条件较为苛刻,从表1可见,IFOA-RBF方法具有较高的预测精度,明显提升了RBF网络的泛化预测能力。
6 结语
采用人工神经网络技术能较好的解决混凝土抗压强度这一高度非线性规律问题,将果蝇优化算法FOA与RBF神经网络相结合,并进行改进的建立IFOA-RBF算法模型用于混凝土抗压强度预测,既体现了RBF网络的广泛映射能力,又明显的提高了网络的泛化能力,具有较高的预测精度。实验结果表明该模型可在混凝土工程中进行实际应用与控制。
参考文献:
[1]季韬,林挺伟,林旭健.基于人工神经网络的混凝土抗压强度预测方法[J].建筑材料学报,2005,(6):676-681.
[2]PAN W T.A new fruit fly optimization algorithm:Taking the finan-cial distress model as an example[J].Knowledge--Based Systems,2012,(2):69-74.
[3]潘文超.果蝇最佳化演算法[M].台北:沧海书局,2011:10-12.
[4]潘文超.应用果蝇优化算法优化广义回归神经网络进行企业经营绩效评估[J].太原理工大学学报(社会科学版),2011,(4):1-4.
[5]李泓泽,郭森,李春杰.果蝇优化最小二乘支持向量机混合预测模型——以我国物流需求量预测为例[J].经济数学,2012,(3):103-106.
[6]刘翠玲,张路路,王进旗,等.基于FOA-GRNN油井计量原油含水率的预测[J].计算机仿真,2012,(11):243-246.
[7]许智慧,王福林,孙丹丹,等.基于FOA-RBF神经网络的外贸出口预测[J].数学的实践与认识,2012,(13):14-19.
[8]徐富强,刘相国.基于优化的RBF神经网络的变量筛选方法[J].计算机系统应用,2012,(3):206-208;王晓伟.基于RBF网络的混凝土抗压强度的预测[J].筑路机械与施工机械化,2006,(10):23-26.
[9]YEH I C.Modeling of strength of high performance concrete using artificial neural networks[J],Cement and Concrete Research,1998,(28):1797-1808.
[10]皮文山,周红标,胡金平.基于BP神经网络混凝土抗压强度预测[J].低温建筑技术,2011,(4):14-16.
[11]廖小辉,黄新,施俊玲,等.基于BP网络的再生混凝土抗压强度的预测模型[J].南京林业大学学报(自然科学版),2010,(5): 105-108.
[12]何晓凤.基于PSO—BP神经网络的混凝土抗压强度预测术[J].微型机与应用,2011,(20):87-90.
ON THE PREDICTION OF CONCRETE COMPRESSIVE STRENGTH BASED ON THE ALGORITHM OF IFOA-RBF
XU Fu-qiang1TAO You-tian1,2,3
(1 Department of Mathematics,Chaohu College,Chaohu Anhui 238000)
(2 Postdoctoral Research Station for School of Mathematics Sciences,USTC,Hefei Anhui 230026)
(3 Postdoctoral Workstation for Anhui Fuhuang Steel Structure Co.Ltd.,Chaohu Anhui 238076)
In order to improve the accuracy of predicting the concrete compressive strength,an IFOA-RBF forecasting model for predicting the concrete compressive strength is established through improving the IFOA and optimizing the Spread value of RBF neural network.The model uses the concrete compressive strength data in UCI database as an example,and the simulation testing is carried out by setting the content of cement,blast furnace slag,fly ash,water,water reducer,coarse aggregate and fine aggregate in per cubic concrete and using days of their placement as the network input, and meanwhile the concrete compressive strength value is used as the network output.Then this paper compares the results with the conclusion of the references.The results show that: the optimized RBF network not only embodies the extensive mapping ability, but also significantly improves the network generalization ability.The validity of the IFOA-RBF model in concrete compressive strength prediction is verified.
FOA;RBF neural network;parameter optimization;concrete compressive strength
TP18
A
1672-2868(2014)06-0007-05
责任编辑:陈 侃
2014-07-15
安徽高校省级自然科学研究项目(项目编号:KJ2013Z230);大学数学基础课程教学团队(项目编号:ch12td01)
徐富强(1984-),男,安徽宣城人。巢湖学院数学系,讲师。研究方向:智能算法、人工神经网络。

